神经网络求导
本篇本来是想写神经网络反向传播算法,但感觉光写这个不是很完整,所以就在前面将相关的求导内容一并补上。所谓的神经网络求导,核心是损失函数对线性输出 z(z=Wa+b)z(z=Wa+b) 求导,即反向传播中的 δ=∂L∂zδ=∂L∂z ,求出了该值以后后面的对参数求导就相对容易了。
JacobianJacobian 矩阵
函数 f:Rn→Rmf:Rn→Rm ,则 JacobianJacobian 矩阵为:
∂f∂x=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢∂f1∂x1∂f2∂x1⋮∂fm∂x1∂f1∂x2∂f2∂x2⋮∂fm∂x2⋯⋯⋱⋯∂f1∂xn∂f2∂xn∂fm∂xn⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥∈Rm×n∂f∂x=[∂f1∂x1∂f1∂x2⋯∂f1∂xn∂f2∂x1∂f2∂x2⋯∂f2∂xn⋮⋮⋱∂fm∂x1∂fm∂x2⋯∂fm∂xn]∈Rm×n
即 (∂f∂x)ij=∂fi∂xj(∂f∂x)ij=∂fi∂xj
神经网络中的激活函数多为对应元素运算 ( element-wise ) ,设输入为K维向量 x=[x1,x2,...,xK]Tx=[x1,x2,...,xK]T , 输出为K维向量 z=[z1,z2,...,zK]Tz=[z1,z2,...,zK]T ,则激活函数为 z=f(x)z=f(x) ,即 zi=[f(x)]i=f(xi)zi=[f(x)]i=f(xi) ,则其导数按 JacobianJacobian 矩阵的定义为一个对角矩阵:
∂f(x)∂x=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢∂f(x1)∂x1∂f(x2)∂x1⋮∂f(xk)∂x1∂f(x1)∂x2∂f(x2)∂x2⋮∂f(xk)∂x2⋯⋯⋱⋯∂f(x1)∂xk∂f(x2)∂xk∂f(xk)∂xk⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎢f′(x1)0⋮00f′(x2)⋮0⋯⋯⋱⋯00f′(xk)⎤⎦⎥⎥⎥⎥⎥=diag(f′(x))∈Rk×k∂f(x)∂x=[∂f(x1)∂x1∂f(x1)∂x2⋯∂f(x1)∂xk∂f(x2)∂x1∂f(x2)∂x2⋯∂f(x2)∂xk⋮⋮⋱∂f(xk)∂x1∂f(xk)∂x2⋯∂f(xk)∂xk]=[f′(x1)0⋯00f′(x2)⋯0⋮⋮⋱00⋯f′(xk)]=diag(f′(x))∈Rk×k
SigmoidSigmoid 激活函数
SigmoidSigmoid 函数的形式为:
σ(z)=11+e−z∈(0,1)σ(z)=11+e−z∈(0,1)
其导数为:
σ′(z)=−(1+e−z)′(1+e−z)2=−−e−z(1+e−z)2=e−z1+e−z⋅11+e−z=σ(z)(1−σ(z))σ′(z)=−(1+e−z)′(1+e−z)2=−−e−z(1+e−z)2=e−z1+e−z⋅11+e−z=σ(z)(1−σ(z))
若输入为 K 维向量 z=[z1,z2,...,zK]Tz=[z1,z2,...,zK]T ,根据上文的定义,其导数为
σ′(z)=⎡⎣⎢⎢⎢⎢⎢σ(z1)(1−σ(z1))0⋮00σ(z2)(1−σ(z2))⋮0⋯⋯⋱⋯00σ(zk)(1−σ(zk))⎤⎦⎥⎥⎥⎥⎥=diag(σ(z)⊙(1−σ(z)))σ′(z)=[σ(z1)(1−σ(z1))0⋯00σ(z2)(1−σ(z2))⋯0⋮⋮⋱00⋯σ(zk)(1−σ(zk))]=diag(σ(z)⊙(1−σ(z)))
TanhTanh 激活函数
TanhTanh 函数可以看作是放大并平移的 SigmoidSigmoid 函数,但因为是零中心化的 (zero-centered) ,通常收敛速度快于 SigmoidSigmoid 函数,下图是二者的对比:
tanh(z)=ez−e−zez+e−z=21+e−2z−1=2σ(2z)−1∈(−1,1)tanh(z)=ez−e−zez+e−z=21+e−2z−1=2σ(2z)−1∈(−1,1)

其导数为:
tanh′(z)=(ez+e−z)2−(ez−e−z)2(ez+e−z)2=1−tanh2(z)tanh′(z)=(ez+e−z)2−(ez−e−z)2(ez+e−z)2=1−tanh2(z)
SoftplusSoftplus 激活函数
SoftplusSoftplus 函数可以看作是 ReLUReLU 函数的平滑版本,形式为:
softplus(z)=log(1+ez)softplus(z)=log(1+ez)

而其导数则恰好就是 SigmoidSigmoid 函数:
softplus′(z)=ez1+ez=11+e−zsoftplus′(z)=ez1+ez=11+e−z
SoftmaxSoftmax 激活函数
softmaxsoftmax 函数将多个标量映射为一个概率分布,其形式为:
yi=softmax(zi)=ezi∑Ck=1ezkyi=softmax(zi)=ezi∑k=1Cezk
yiyi 表示第 ii 个输出值,也可表示属于类别 ii 的概率, ∑i=1Cyi=1∑i=1Cyi=1。
首先求标量形式的导数,即第 ii 个输出对于第 jj 个输入的偏导:
∂yi∂zj=∂ezi∑Ck=1eak∂zj∂yi∂zj=∂ezi∑k=1Ceak∂zj
其中 eziezi 对 zjzj 求导要分情况讨论,即:
∂ezi∂zj={ezi,0,ifi=jifi≠j∂ezi∂zj={ezi,ifi=j0,ifi≠j
那么当 i=ji=j 时:
∂yi∂zj=ezi∑Ck=1ezk−eziezj(∑Ck=1ezk)2=ezi∑Ck=1ezk−ezi∑Ck=1ezkezj∑Ck=1ezk=yi−yiyj(1.1)(1.1)∂yi∂zj=ezi∑k=1Cezk−eziezj(∑k=1Cezk)2=ezi∑k=1Cezk−ezi∑k=1Cezkezj∑k=1Cezk=yi−yiyj
当 i≠ji≠j 时:
∂yi∂zj=0−eziezj(∑Ck=1ezk)2=−yiyj(1.2)(1.2)∂yi∂zj=0−eziezj(∑k=1Cezk)2=−yiyj
于是二者综合:
∂yi∂zj=1{i=j}yi−yiyj(1.3)(1.3)∂yi∂zj=1{i=j}yi−yiyj
其中 1{i=j}={1,0,ifi=jifi≠j1{i=j}={1,ifi=j0,ifi≠j
当 softmaxsoftmax 函数的输入为K 维向量 z=[z1,z2,...,zK]Tz=[z1,z2,...,zK]T 时,转换形式为 RK→RKRK→RK :
y=softmax(z)=1∑Kk=1ezk⎡⎣⎢⎢⎢⎢ez1ez2⋮ezK⎤⎦⎥⎥⎥⎥y=softmax(z)=1∑k=1Kezk[ez1ez2⋮ezK]
其导数同样为 JabocianJabocian 矩阵 ( 同时利用 (1.1)(1.1) 和 (1.2)(1.2) 式 ):
∂y∂z=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢∂y1∂z1∂y2∂z1⋮∂yK∂z1∂y1∂z2∂y2∂z2⋮∂yK∂z2⋯⋯⋱⋯∂y1∂zK∂y2∂zK∂yK∂zK⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎢y1−y1y1−y2y1⋮−yKy1−y1y2y2−y2y1⋮−yKy2⋯⋯⋱⋯−y1yK−y2yKyK−yKyK⎤⎦⎥⎥⎥⎥⎥=diag(y)−yyT=diag(softmax(z))−softmax(z)softmax(z)T∂y∂z=[∂y1∂z1∂y1∂z2⋯∂y1∂zK∂y2∂z1∂y2∂z2⋯∂y2∂zK⋮⋮⋱∂yK∂z1∂yK∂z2⋯∂yK∂zK]=[y1−y1y1−y1y2⋯−y1yK−y2y1y2−y2y1⋯−y2yK⋮⋮⋱−yKy1−yKy2⋯yK−yKyK]=diag(y)−yyT=diag(softmax(z))−softmax(z)softmax(z)T
交叉熵损失函数
交叉熵损失有两种表示形式,设真实标签为 yy ,预测值为 aa :
(一) yy 为标量,即 y∈Ry∈R ,则交叉熵损失为:
L(y,a)=−∑j=1k1{y=j}logajL(y,a)=−∑j=1k1{y=j}logaj
(二) yy 为one-hot向量,即 y=[0,0...1...0]T∈Rky=[0,0...1...0]T∈Rk ,则交叉熵损失为:
L(y,a)=−∑j=1kyjlogajL(y,a)=−∑j=1kyjlogaj
交叉熵损失函数 + Sigmoid激活函数
已知 L(y,a)=−∑j=1kyjlogajL(y,a)=−∑j=1kyjlogaj, aj=σ(zj)=11+e−zjaj=σ(zj)=11+e−zj ,求 ∂Lzj∂Lzj :
∂L∂zj=∂L∂aj∂aj∂zj=−yj1σ(zj)σ(zj)(1−σ(zj))=σ(zj)−1=aj−yj∂L∂zj=∂L∂aj∂aj∂zj=−yj1σ(zj)σ(zj)(1−σ(zj))=σ(zj)−1=aj−yj
交叉熵损失函数 + Softmax激活函数
已知 L(y,a)=−∑i=1kyilogaiL(y,a)=−∑i=1kyilogai, aj=softmax(zj)=ezj∑Cc=1ezcaj=softmax(zj)=ezj∑c=1Cezc ,求 ∂L∂zj∂L∂zj :
∂L∂zj=∑i=1k∂L∂ai∂ai∂zj=∑i=j∂L∂aj∂aj∂zj+∑i≠j∂L∂ai∂ai∂zj=−yjaj∂aj∂zj−∑i≠jyiaiaizj=−yjajaj(1−aj)+∑i≠jyiaiaiaj运用 (1.1)和(1.2) 式=−yj+yjaj+∑i≠jyiaj=aj−yj∂L∂zj=∑i=1k∂L∂ai∂ai∂zj=∑i=j∂L∂aj∂aj∂zj+∑i≠j∂L∂ai∂ai∂zj=−yjaj∂aj∂zj−∑i≠jyiaiaizj=−yjajaj(1−aj)+∑i≠jyiaiaiaj运用 (1.1)和(1.2) 式=−yj+yjaj+∑i≠jyiaj=aj−yj
若输入为 KK 维向量 z=[z1,z2,...,zk]Tz=[z1,z2,...,zk]T ,则梯度为:
∂L∂z=a−y=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢a1−0⋮aj−1⋮ak−0⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥∂L∂z=a−y=[a1−0⋮aj−1⋮ak−0]
另外运用对数除法运算,上面的求导过程可以简化:
L(y,a)=−∑i=1kyilogai=−∑i=1kyilogezi∑cezc=−∑i=1kyizi+yilog∑cezcL(y,a)=−∑i=1kyilogai=−∑i=1kyilogezi∑cezc=−∑i=1kyizi+yilog∑cezc
∂L∂zi=−yi+ezi∑cezc=ai−yi∂L∂zi=−yi+ezi∑cezc=ai−yi
神经网络反向传播算法
通常所谓的“学习”指的是通过最小化损失函数进而求得相应参数的过程,神经网络中一般采用梯度下降来实现这个过程,即:
θ=θ−α⋅∂∂θL(θ)θ=θ−α⋅∂∂θL(θ)
用神经网络中的常用参数符号替换,并用矩阵形式表示:
W(l)b(l)=W(l)−α∂L∂W(l)=b(l)−α∂L∂b(l)W(l)=W(l)−α∂L∂W(l)b(l)=b(l)−α∂L∂b(l)
其中 (l)(l) 表示第 ll 层。
导数是梯度的组成部分,通常采用数值微分的方法近似下式:
f′(x)=limh→0f(x+h)−f(x)hf′(x)=limh→0f(x+h)−f(x)h
f′(x)f′(x) 表示函数 f(x)f(x) 在 xx 处的斜率,但是由于运算时 hh 不可能无限接近于零,上式容易引起数值计算问题,所以实际中常采用中心差分来近似:
f′(x)=limh→0f(x+h)−f(x−h)2hf′(x)=limh→0f(x+h)−f(x−h)2h
这样整个梯度的计算可以用以下代码实现:
<span style="color:#000000"><code><span style="color:#0000ff">import</span> numpy <span style="color:#0000ff">as</span> np
<span style="color:#0000ff">def</span> <span style="color:#a31515">numerical_gradient</span>(f, x): <span style="color:green"># f为函数,x为输入向量</span>
h = 1e-4
grad = np.zeros_like(x)
it = np.nditer(x, flags=[<span style="color:#a31515">'multi_index'</span>], op_flags=[<span style="color:#a31515">'readwrite'</span>])
<span style="color:#0000ff">while</span> <span style="color:#0000ff">not</span> it.finished:
idx = it.multi_index
temp = x[idx]
x[idx] = temp + h
fxh1 = f(x)
x[idx] = temp - h
fxh2 = f(x)
grad[idx] = (fxh1 + fxh2) / (2*h)
x[idx] = temp
it.iternext()
<span style="color:#0000ff">return</span> grad</code></span>
由于数值微分对每个参数都要计算 f(x+h)f(x+h) 和 f(x−h)f(x−h) ,假设神经网络中有100万个参数,则需要计算200万次损失函数。如果是使用 SGD,则是每个样本计算200万次,显然是不可承受的。所以才需要反向传播算法这样能够高效计算梯度的方法。
接下来先定义神经网络中前向传播的式子 (ll 表示隐藏层, LL 表示输出层):

z(l)=W(l)a(l−1)+b(l)a(l)=f(z(l))y^=a(L)=f(z(L))L=L(y,y^)(2.1)(2.2)(2.3)(2.4)(2.1)z(l)=W(l)a(l−1)+b(l)(2.2)a(l)=f(z(l))(2.3)y^=a(L)=f(z(L))(2.4)L=L(y,y^)
现在我们的终极目标是得到 ∂L∂W(l)∂L∂W(l) 和 ∂L∂b(l)∂L∂b(l) ,为了计算方便,先来看各自的分量 ∂L∂W(l)jk∂L∂Wjk(l) 和 ∂L∂b(l)j∂L∂bj(l) 。
这里定义 δ(l)j=∂L∂z(l)jδj(l)=∂L∂zj(l) , 根据 (2.1)(2.1) 式使用链式法则:
∂L∂W(l)jk=∂L∂z(l)j∂z(l)j∂W(l)jk=δ(l)j∂∂W(l)jk(∑iW(l)jia(l−1)i)=δ(l)ja(l−1)k∂L∂b(l)j=∂L∂z(l)j∂z(l)j∂b(l)j=δ(l)j(2.5)(2.6)(2.5)∂L∂Wjk(l)=∂L∂zj(l)∂zj(l)∂Wjk(l)=δj(l)∂∂Wjk(l)(∑iWji(l)ai(l−1))=δj(l)ak(l−1)(2.6)∂L∂bj(l)=∂L∂zj(l)∂zj(l)∂bj(l)=δj(l)
所以接下来的问题就是求 δ(l)jδj(l) :
(1) 对于输出层 LL :
δLj=∂L∂z(L)j=∂L∂a(L)j∂a(L)j∂z(L)j=∂L∂a(L)jf′(z(L)j)(2.7)(2.7)δjL=∂L∂zj(L)=∂L∂aj(L)∂aj(L)∂zj(L)=∂L∂aj(L)f′(zj(L))
(2) 对于隐藏层 ll ,由 (2.1)(2.1) 式可知:
⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪z(l+1)1z(l+1)2z(l+1)k=∑jW(l+1)1ja(l)j+b(l+1)1=∑jW(l+1)2ja(l)j+b(l+1)2⋮=∑jW(l+1)kja(l)j+b(l+1)k{z1(l+1)=∑jW1j(l+1)aj(l)+b1(l+1)z2(l+1)=∑jW2j(l+1)aj(l)+b2(l+1)⋮zk(l+1)=∑jWkj(l+1)aj(l)+bk(l+1)
可见 a(l)jaj(l) 对于 z(l+1)z(l+1) 的每个分量都有影响,使用链式法则时需要加和每个分量,下图是一个形象表示:
所以下面求 δ(l)jδj(l) 时会用 kk 加和:
δ(l)j=∂L∂z(l)j=⎛⎝∑k∂L∂z(l+1)k∂z(l+1)k∂a(l)j⎞⎠∂a(l)j∂z(l)j=⎛⎝⎜⎜⎜⎜⎜∑k∂L∂z(l+1)k∂(∑jW(l+1)kja(l)j+b(l+1)k)∂a(l)j⎞⎠⎟⎟⎟⎟⎟∂a(l)j∂z(l)j=(∑kδ(l+1)kW(l+1)kj)f′(z(l)j)(2.8)δj(l)=∂L∂zj(l)=(∑k∂L∂zk(l+1)∂zk(l+1)∂aj(l))∂aj(l)∂zj(l)=(∑k∂L∂zk(l+1)∂(∑jWkj(l+1)aj(l)+bk(l+1))∂aj(l))∂aj(l)∂zj(l)(2.8)=(∑kδk(l+1)Wkj(l+1))f′(zj(l))
将上面的 (2.5)∼(2.8)(2.5)∼(2.8) 式写成矩阵形式,就得到了传说中反向传播算法的四大公式:
δ(L)=∂L∂z(L)=∇a(L)L⊙f′(z(L))δ(l)=∂L∂z(l)=((W(l+1))Tδ(l+1))⊙f′(z(l))∂L∂W(l)=δ(l)(a(l−1))T=⎡⎣⎢⎢⎢⎢⎢⎢⎢δ(l)1a(l−1)1δ(l)2a(l−1)1⋮δ(l)ja(l−1)1δ(l)1a(l−1)2δ(l)2a(l−1)2⋮δ(l)ja(l−1)2⋯⋯⋱⋯δ(l)1a(l−1)kδ(l)2a(l−1)kδ(l)ja(l−1)k⎤⎦⎥⎥⎥⎥⎥⎥⎥∂L∂b(l)=δ(l)δ(L)=∂L∂z(L)=∇a(L)L⊙f′(z(L))δ(l)=∂L∂z(l)=((W(l+1))Tδ(l+1))⊙f′(z(l))∂L∂W(l)=δ(l)(a(l−1))T=[δ1(l)a1(l−1)δ1(l)a2(l−1)⋯δ1(l)ak(l−1)δ2(l)a1(l−1)δ2(l)a2(l−1)⋯δ2(l)ak(l−1)⋮⋮⋱δj(l)a1(l−1)δj(l)a2(l−1)⋯δj(l)ak(l−1)]∂L∂b(l)=δ(l)
而 δ(l)δ(l) 的计算可以直接套用上面损失函数 + 激活函数的计算结果。
反向传播算法 + 梯度下降算法流程
(1) 前向传播阶段:使用下列式子计算每一层的 z(l)z(l) 和 a(l)a(l) ,直到最后一层。
z(l)=W(l)a(l−1)+b(l)a(l)=f(z(l))y^=a(L)=f(z(L))L=L(y,y^)z(l)=W(l)a(l−1)+b(l)a(l)=f(z(l))y^=a(L)=f(z(L))L=L(y,y^)
(2) 反向传播阶段:
(2.1) 计算输出层的误差: δ(L)=∇a(L)L,⊙f′(z(L))δ(L)=∇a(L)L,⊙f′(z(L))
(2.2) 由后一层反向传播计算前一层的误差: δ(l)=((W(l+1))Tδ(l+1))⊙f′(z(l))δ(l)=((W(l+1))Tδ(l+1))⊙f′(z(l))
(2.3) 计算梯度: ∂L∂W(l)=δ(l)(a(l−1))T∂L∂W(l)=δ(l)(a(l−1))T , ∂L∂b(l)=δ(l)∂L∂b(l)=δ(l)
(3) 参数更新:
W(l)b(l)=W(l)−α∂L∂W(l)=b(l)−α∂L∂b(l)W(l)=W(l)−α∂L∂W(l)b(l)=b(l)−α∂L∂b(l)







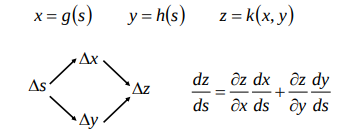













 2308
2308











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








