数据挖掘之关联分析六（子图模式）

子图模式

频繁子图挖掘（frequent subgraph mining）：在图的集合中发现一组公共子结构。

图和子图

图是一种用来表示实体集之间联系的数据结构。

子图，图        

是另一个图   的子图，如果它的顶点集V'是V的子集，并且它的边集E'是E的子集，子图关系记做    

。

支持度，给定图的集族  

, 子图   的支持度定义为包含它的所有图所占的百分比。

          

频繁子图挖掘

频繁子图挖掘 给定集合  

和支持度阈值   ，频繁子图挖掘的目标是找出使得所有   的子图  

.

该定义适用于所有类型的图，但是本章主要关注无向连通图（undirected，connected graph）。定义如下

1. 一个图是连通你的，如果图中每对顶点之间都存在一条路径。
2. 一个图是无向的，如果它只包含无向边。

挖掘频繁子图的是计算量很大的任务，对于d个实体的数据集，子图总数为

         

其中，      是选择i个顶点形成的子图方法数，    

是子图的顶点之间边的最大值。

候选的子图很多，但不连通的子图通常被忽略，因为它们没有连通子图令人感兴趣。
频繁子图挖掘的一种蛮力方法是，产生所有连通子图作为候选，并计算各自的支持度。候选子图比传统的候选项集的个数大得多的原因为

1. 项在项集中之多出现一次，而某个标号可能在一个图中出现多次。
2. 相同的顶点标号对可以有多重边标号选择。

给定大量候选子图，即使对于规模适应的图，蛮力方法也可能垮掉

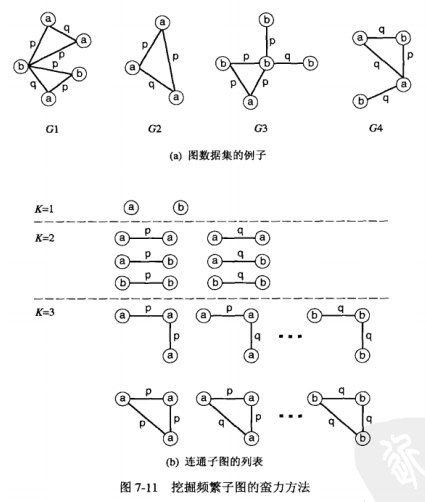
类Apriori方法

1.数据变换，一种方法是将图变换为类似事务的形式，使得我们可以使用诸如Apriori等已有的算法。在这种情况下，边标号和对应的顶点标号      

组合被映射到一个项。事务的宽度由图的边数决定。但是，只有当图中每一条边都具有唯一的顶点和边标号组合时，该方法才可行。

2.频繁子图挖掘算法的一般结构
挖掘频繁子图的类Apriori算法由以下步骤组成，

1. 候选产生：合并频繁（k-1）-子图对，得到候选k-子图。
2. 候选剪枝：丢弃包含非频繁的(k-1)-子图的所有候选k-子图。
3. 支持度计数：统计  

3. 中包含每个候选的图的个数。
4. 候选删除：丢弃支持度小于minsup的所有候选子图。

候选产生

在候选产生阶段，合并(k-1)-子图为k-子图，首要问题是如何定义子图的大小k。通过添加一个顶点，迭代地扩展子图的方法称作顶点增长（vertex growing）。k也可以是图中边的个数，添加一条边到已有的子图中来扩展子图的方法称作边增长（edge growing）。

为了避免产生重复的候选，我们可以对合并施加条件：两个(k-1)-子图必须共享一个共同的(k-2)-子图，共同的子图称为核（core）。

1.通过顶点增长来产生候选
通过添加一个新的结点到已经存在的一个频繁子图上来产生候选。可以使用邻接矩阵来表示图，每一项M（i,j）为链接    

和    

的的边或者0。

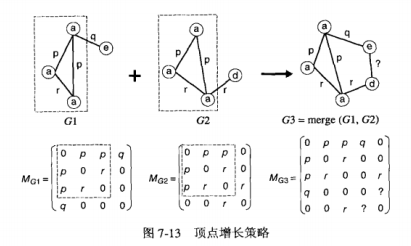
合并过程：
邻接矩阵    

与另一个邻接矩阵     合并，如果删除     和     的最后一行和最后一列得到的子矩阵相同，结果得到的候选矩阵为在     后面添加     的最后一行和最后，新矩阵的其余项为0，或者连接顶点对的合法标号替换。
上面图中合并后得到的  

的？边可以通过考虑所有可能的边标号从而大大增加了候选的子图个数。

2.通过边增长产生候选
变增长将一个新的边插入到一个已经存在的频繁子图中。与顶点增长不同，结果子图的顶点个数不一定增长。

边增长合并过程：
一个频繁子图    

和另一个频繁子图     合并，仅当从     删除一条边后得到的子图与从     中删除一条边后得到的子图的拓扑等价，合并后的结果是     添加    

那条二外的边。

拓扑等价：

G1中的每个顶点都等价，G2中有两对顶点等价：    

与     ，     与    

。G3没有等价顶点。

下面两个(k-1)-子图G1和G2，相同的核用矩形框表示

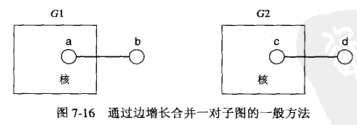
根据a与c是否相等和b与d是否相等，合并得到的结果有

当一对(k-1)-子图相同的核有多个时，会产生更多的候选子图，如下所示，有两个相同的核

候选剪枝

需要剪去(k-1)-子图非频繁的候选。候选剪枝可以，通过以下方式实现。
相继从k-子图中删除一条边，并检查得到的(k-1)-子图是否连通且频繁。如果不是，则舍弃。
为了检查(k-1)子图是否频繁，需要将其与其他的(k-1)-子图匹配。判定连个图是够拓扑等价，即图同构。

处理图同构
处理图同构的问题的标准方法是，将每个图都映射到一个唯一的串表达式，称作代码或规范标号（canonical label）。如果两个图是同构的，则它们的代码一定相同。这个性质可以使得我们通过比较图的规范编号来检查图同构。

构造图的规范标号的第一步是找出图的邻接矩阵表示。可利用矩阵中的基本矩阵进行行列互换。
第二步是确定每个邻接矩阵的串表示，由于邻接举证是串表示的，因此只需要根据矩阵的上三角阵部分构造串就足够了。
第三步比较图的所有串表示，并选出具有最小（最大）字典序值的串，确保每个图的字符串唯一。

支持度计数

支持度计数对于每个  

，必须确保包含G中的所有候选子图。加快的策略是维护一个与每个频繁(k-1)-子图相关联的图ID表，如果新的候选k-子图通过合并一对拼单(k-1)-子图而生成，就对它们的对应图ID表求交集。最后，子图同构检查就在表中的图上进行，确定它们是否包含特定的子图。