2017.11.5与章丘四中互测莱芜试题

题目背景（后来临时补的）比较长我就不粘了。

Problem 1 ：第一题

题目描述
一个序列上共有 n 个点，两两之间形成一条线段,任意选择其中 k 条线段，使得这 k 条线段的长度和最小（k 条线段端点不能重合）。

输入格式
第一行两个整数 n k
接下来 n 行每行一个整数表示每个点在序列上的坐标。

输出格式
一行一个整数表示这个最小的和。

样例输入
5 2
1
3
4
6
12

样例输出
4

数据范围及提示
对于 30%数据 n ≤ 20
对于 60%数据 n ≤ 100
对于 100%数据 n ≤ 1000, k ≤ n/2

思路
见Codevs1615数据备份：
http://blog.csdn.net/qq_36693533/article/details/78472780
这个数据范围DP也可以过…

失误
刚开始考虑二分长度背包验证…但后来才发现有后效性…
若考虑当前选或不选会产生后效性，
可以尝试改变策略，着眼于后一状态,由前一状态转移。

Problem 2 ：第二题

题目描述
给定一个 n+1 个点（编号为 0,1,2..n）的有向图，求从 0 号点出发，经过所有城市至少一次，且最后回到 0 号点的最短路。

输入格式
一行一个整数 n
接下来一个(n + 1)* (n + 1)的邻接矩阵表示城市两两之间的路径（a 到 b 的路径
长度不一定等于 b 到 a 的路径长度）

输出格式
一个整数表示最短路径。

样例输入
3
0 1 10 10
1 0 1 2
10 1 0 10
10 2 10 0

样例输出
8

数据范围及提示
1 ≤ n ≤ 15

思路
分层图（状压）最短路，或状压DP。
具体请看注释

代码——分层图最短路版本

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
using namespace std;
int n,t,tot;
int first[200010],nxt[200010];
int dis[20][100010],inq[20][100010];//二进制压位记录经过了哪些点。
struct edge
{
    int u,v,w;
}l[200010];
struct st
{
    int A,Z;
};
queue<st>q;
void build(int f,int t,int c)
{
    l[++tot]=(edge){f,t,c};
    nxt[tot]=first[f];
    first[f]=tot;
}
void SPFA()
{
    memset(dis,0X7f,sizeof(dis));
    memset(inq,0,sizeof(inq));
    while(!q.empty())
    q.pop(); 
    dis[0][1<<0]=0;//清晰 
    inq[0][1<<0]=1;
    q.push((st){0,1<<0});
    while(!q.empty())
    {
        st k=q.front();
        q.pop();
        inq[k.A][k.Z]=0;
        for(int i=first[k.A];i!=-1;i=nxt[i])
        {
            int x=l[i].v;
            if(dis[x][k.Z|(1<<x)]>dis[k.A][k.Z]+l[i].w)
            //或运算:如果是第一次走到,则更新已有状态,或者用if(k.Z&(1<<x))判断是否更新状态 
            {                                          
                dis[x][k.Z|(1<<x)]=dis[k.A][k.Z]+l[i].w;
                if(!inq[x][k.Z|(1<<x)])
                {
                    q.push((st){x,k.Z|(1<<x)});
                    inq[x][k.Z|(1<<x)]=1;
                }
            }
        }
    }
}
int main()
{
    memset(first,-1,sizeof(first));
    scanf("%d",&n);
    for(int i=1;i<=n+1;i++)
    {
        for(int j=1;j<=n+1;j++)
        {
            scanf("%d",&t);
            build(i-1,j-1,t);
        }
    }
    SPFA();
    int tmp=0;
    for(int i=0;i<=n;i++)
    tmp=(tmp|(1<<i));//计算标准状态
    printf("%d",dis[0][tmp]);//一定会回到0号点 
    return 0;               //或者还有更机智的写法:dis[0][(1<<(n+1))-1] 
}

代码——状压DP版本

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
const int INF = 2139062143;
int n,aim,ans;
int dis[1010][1010],dp[30][50010];
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n+1;i++)
    {
        for(int j=1;j<=n+1;j++)
        scanf("%d",&dis[i-1][j-1]);
    }
    for(int k=0;k<n;k++)//floyd
    {
        for(int i=0;i<n;i++)
        {
            for(int j=0;j<n;j++)
            dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
        }
    }
    aim=(1<<n)-1;
    memset(dp,0x7f,sizeof(dp));
    dp[0][0]=0;
    for(int j=0;j<=aim;j++)//枚举状态 
    {
        for(int i=0;i<=n;i++)//枚举中间点 
        {
            if(dp[i][j]<INF)//若当前状况可以用来更新 
            {
                for(int k=1;k<=n;k++)//枚举终点 
                dp[k][j|(1<<k-1)]=min(dp[k][j|(1<<k-1)],dp[i][j]+dis[i][k]);
            }
        }
    }
    ans=1e9+7;
    for(int i=1;i<=n;i++)
    ans=min(ans,dp[i][aim]+dis[i][0]);
    //从起点经过所有点到当前点的距离+当前点到起点的距离 
    printf("%d",ans);
    return 0; 
}

Problem 3：

题目描述
给定 n 个点及其坐标，每个点坐标均为非负整数。现在要删除其中 k 个，使得
剩下的点两两之间距离的最大值最小，两点之间距离为欧几里得距离，即


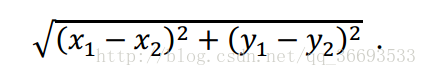
输入格式
第一行两个整数 n， k
接下来 n 行每行两个整数描述一个点的坐标，这些点按照顺序进行编号，编号
为 1 – n

输出格式
一行 k 个数，表示需要删除的点的编号，如果有多解，输出任意一组

样例输入1
5 2
1 2
0 0
2 2
1 1
3 3

样例输出 1
2 5

样例输入 2
4 1
0 0
0 0
1 1
1 1

样例输出 2
2

样例解释 1
删除 2 号点与 5 号点后， 最大距离为 3 号与 4 号点距离≈1.41421

样例解释 2
删除任意一点后，两点之间的最大值都≈1.41421，所以输出任意一点都正确。

数据范围及提示


思路
二分最远距离是多长，把大于这个距离的两点之间建边，然后把大于这个距离的边删去， 也就是删掉两个端点中至少 1 个， 看删除 k 个点后，是否能把所有边删去。
问题变成了无向图最小点覆盖问题。
这是一个NPC问题，但k非常小，于是我们可以爆搜，枚举删去哪 k 个点。但要注意剪枝：
1. 考虑如果一个点不删的话， 那么与它相邻的所有点必须要删去。
这样做还是不够优。
2. 如果一个点的度数为 1， 那么就没有必要删这个点，直接删对面的
点，因为删对面的点， 结果一定不会更差。
这样每次验证的时间复杂度是 O（fib（k））