简介
NaïveBayes算法,又叫朴素贝叶斯算法,朴素:特征条件独立;贝叶斯:基于贝叶斯定理。属于监督学习的生成模型,实现简单,没有迭代,并有坚实的数学理论(即贝叶斯定理)作为支撑。在大量样本下会有较好的表现,不适用于输入向量的特征条件有关联的场景。
基本思想
(1)病人分类的例子
某个医院早上收了六个门诊病人,如下表:
症状 职业 疾病
——————————————————
打喷嚏 护士 感冒
打喷嚏 农夫 过敏
头痛 建筑工人 脑震荡
头痛 建筑工人 感冒
打喷嚏 教师 感冒
头痛 教师 脑震荡
现在又来了第七个病人,是一个打喷嚏的建筑工人。请问他患上感冒的概率有多大?
根据贝叶斯定理:
P(A|B) = P(B|A) P(A) / P(B)
可得
P(感冒|打喷嚏x建筑工人)
= P(打喷嚏x建筑工人|感冒) x P(感冒) / P(打喷嚏x建筑工人)
假定”打喷嚏”和”建筑工人”这两个特征是独立的,因此,上面的等式就变成了
P(感冒|打喷嚏x建筑工人)
= P(打喷嚏|感冒) x P(建筑工人|感冒) x P(感冒) / P(打喷嚏) x P(建筑工人)
这是可以计算的。
P(感冒|打喷嚏x建筑工人)
= 0.66 x 0.33 x 0.5 / 0.5 x 0.33
= 0.66
因此,这个打喷嚏的建筑工人,有66%的概率是得了感冒。同理,可以计算这个病人患上过敏或脑震荡的概率。比较这几个概率,就可以知道他最可能得什么病。
这就是贝叶斯分类器的基本方法:在统计资料的基础上,依据某些特征,计算各个类别的概率,从而实现分类。
(2)朴素贝叶斯分类器的公式
假设某个体有n项特征(Feature),分别为F1、F2、…、Fn。现有m个类别(Category),分别为C1、C2、…、Cm。贝叶斯分类器就是计算出概率最大的那个分类,也就是求下面这个算式的最大值:
P(C|F1F2...Fn) = P(F1F2...Fn|C)P(C) / P(F1F2...Fn)
由于 P(F1F2…Fn) 对于所有的类别都是相同的,可以省略,问题就变成了求
P(F1F2...Fn|C)P(C)
的最大值。
朴素贝叶斯分类器则是更进一步,假设所有特征都彼此独立,因此
P(F1F2...Fn|C)P(C) = P(F1|C)P(F2|C) ... P(Fn|C)P(C)
上式等号右边的每一项,都可以从统计资料中得到,由此就可以计算出每个类别对应的概率,从而找出最大概率的那个类。
虽然”所有特征彼此独立”这个假设,在现实中不太可能成立,但是它可以大大简化计算,而且有研究表明对分类结果的准确性影响不大。
(3)拉普拉斯平滑(Laplace smoothing)
也就是参数为1时的贝叶斯估计,当某个分量在总样本某个分类中(观察样本库/训练集)从没出现过,会导致整个实例的计算结果为0。为了解决这个问题,使用拉普拉斯平滑/加1平滑进行处理。
它的思想非常简单,就是对先验概率的分子(划分的计数)加1,分母加上类别数;对条件概率分子加1,分母加上对应特征的可能取值数量。这样在解决零概率问题的同时,也保证了概率和依然为1。
eg:假设在文本分类中,有3个类,C1、C2、C3,在指定的训练样本中,某个词语F1,在各个类中观测计数分别为=0,990,10,即概率为P(F1/C1)=0,P(F1/C2)=0.99,P(F1/C3)=0.01,对这三个量使用拉普拉斯平滑的计算方法如下:
1/1003 = 0.001,991/1003=0.988,11/1003=0.011
实际应用场景
文本分类
垃圾邮件过滤
病人分类
拼写检查
朴素贝叶斯模型
朴素贝叶斯常用的三个模型有:
高斯模型:处理特征是连续型变量的情况
多项式模型:最常见,要求特征是离散数据
伯努利模型:要求特征是离散的,且为布尔类型,即true和false,或者1和0
代码实现
基于多项式模型的朴素贝叶斯算法(在github获取)
# encoding=utf-8
import pandas as pd
import numpy as np
import cv2
import time
from sklearn.cross_validation import train_test_split
from sklearn.metrics import accuracy_score
# 二值化处理
def binaryzation(img):
cv_img = img.astype(np.uint8) # 类型转化成Numpy中的uint8型
cv2.threshold(cv_img, 50, 1, cv2.THRESH_BINARY_INV, cv_img) # 大于50的值赋值为0,不然赋值为1
return cv_img
# 训练,计算出先验概率和条件概率
def Train(trainset, train_labels):
prior_probability = np.zeros(class_num) # 先验概率
conditional_probability = np.zeros((class_num, feature_len, 2)) # 条件概率
# 计算
for i in range(len(train_labels)):
img = binaryzation(trainset[i]) # 图片二值化,让每一个特征都只有0,1两种取值
label = train_labels[i]
prior_probability[label] += 1
for j in range(feature_len):
conditional_probability[label][j][img[j]] += 1
# 将条件概率归到[1,10001]
for i in range(class_num):
for j in range(feature_len):
# 经过二值化后图像只有0,1两种取值
pix_0 = conditional_probability[i][j][0]
pix_1 = conditional_probability[i][j][1]
# 计算0,1像素点对应的条件概率
probalility_0 = (float(pix_0)/float(pix_0+pix_1))*10000 + 1
probalility_1 = (float(pix_1)/float(pix_0+pix_1))*10000 + 1
conditional_probability[i][j][0] = probalility_0
conditional_probability[i][j][1] = probalility_1
return prior_probability, conditional_probability
# 计算概率
def calculate_probability(img, label):
probability = int(prior_probability[label])
for j in range(feature_len):
probability *= int(conditional_probability[label][j][img[j]])
return probability
# 预测
def Predict(testset, prior_probability, conditional_probability):
predict = []
# 对每个输入的x,将后验概率最大的类作为x的类输出
for img in testset:
img = binaryzation(img) # 图像二值化
max_label = 0
max_probability = calculate_probability(img, 0)
for j in range(1, class_num):
probability = calculate_probability(img, j)
if max_probability < probability:
max_label = j
max_probability = probability
predict.append(max_label)
return np.array(predict)
class_num = 10 # MINST数据集有10种labels,分别是“0,1,2,3,4,5,6,7,8,9”
feature_len = 784 # MINST数据集每个image有28*28=784个特征(pixels)
if __name__ == '__main__':
print("Start read data")
time_1 = time.time()
raw_data = pd.read_csv('../data/train.csv', header=0) # 读取csv数据
data = raw_data.values
features = data[::, 1::]
labels = data[::, 0]
# 避免过拟合,采用交叉验证,随机选取33%数据作为测试集,剩余为训练集
train_features, test_features, train_labels, test_labels = train_test_split(features, labels, test_size=0.33, random_state=0)
time_2 = time.time()
print('read data cost %f seconds' % (time_2 - time_1))
print('Start training')
prior_probability, conditional_probability = Train(train_features, train_labels)
time_3 = time.time()
print('training cost %f seconds' % (time_3 - time_2))
print('Start predicting')
test_predict = Predict(test_features, prior_probability, conditional_probability)
time_4 = time.time()
print('predicting cost %f seconds' % (time_4 - time_3))
score = accuracy_score(test_labels, test_predict)
print("The accruacy score is %f" % score)
测试数据集为MNIST数据集,获取地址train.csv
运行结果
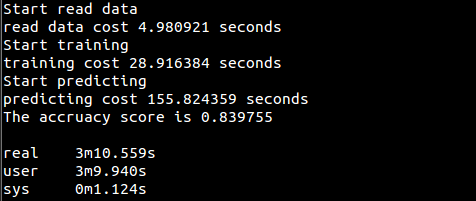
朴素贝叶斯分类
引子
朴素贝叶斯分类是一种常用的分类算法,他根据研究对象的某些特征,来推断出该研究对象属于该研究领域的哪个类别。
数学是解决我们生活中产生的各种问题的。所以,数学源于生活,生活中也处处体现数学,我们编程,不过是把人能够理解的数学知识转换成计算机能够理解的形式来解决实际问题。拿朴素贝叶斯分类来说,其实生活中比比皆是,举个例子:
我们在大街上看到一个人,猜测他属于哪个职业。这就是一种分类,你是根据什么来判断的。可能是根据这个人的穿着打扮,言行举止。
穿着打扮:胡子拉碴、头发乱七八糟,背着大的电脑包
言行举止:双眼无神(估计在想哪个bug的解决办法),黑眼圈重,头发没洗。
所以,我大概能看出这个人职业是程序员(开个玩笑,这只是程序员自黑而已,我身边的程序员都不是这样的,当然也包括我)。
其实穿着打扮、言行举止就是人的特征属性
我们要对某个对象分类,必须根据他的特征属性来判断。
概述
要了解贝叶斯分类,必须了解贝叶斯定理,贝叶斯定理离不开条件概率
条件概率定义:
事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为P(A|B),读作“在B条件下A的概率”。
根据文氏图,可以很清楚地看到在事件B发生的情况下,事件A发生的概率就是P(A∩B)除以P(B)。
根据文氏图,可以很清楚地看到在事件B发生的情况下,事件A发生的概率就是P(A∩B)除以P(B)。
P(A|B)=P(A∩B)/P(B)
因此,
P(A∩B)=P(A|B)P(B)
所以,
P(A|B)P(B)=P(B|A)P(A)
即
P(A|B)=P(B|A)P(A)/P(B)
上面的公式就是贝叶斯定理
生活中,我们经常知道这种情况 ,P(A|B),但是不知道P(B|A).比如:
A: 表示用户收入高
B:表示订购2G流量套餐
P(A|B) 表示订购2G流量套餐的用户收入高的概率,这个可以通过统计的样本算出得到。
但是现在有一个用户收入高(A),他购买2G流量套餐(B)的概率是多少,即P(B|A),这才是我们关注
所以通过贝叶斯定理,我们可以把这两者挂上钩,求出我们想知道的P(B|A)
病人疾病预测分类例子
看一个简单的形式化的列子,来说明贝叶斯分类的作用
这个例子来自:阮一峰老师的介绍贝叶斯应用博文中的一个病人分类的例子
如下:其中特征属性是症状和职业,类别是疾病(包括感冒,过敏、脑震荡)
某个医院早上收了六个门诊病人,如下表。
症状 职业 疾病
打喷嚏 护士 感冒
打喷嚏 农夫 过敏
头痛 建筑工人 脑震荡
头痛 建筑工人 感冒
打喷嚏 教师 感冒
头痛 教师 脑震荡
现在又来了第七个病人,是一个打喷嚏的建筑工人。请问他患上感冒的概率有多大?
根据贝叶斯定理:
P(A|B) = P(B|A) P(A) / P(B)
可得
P(感冒|打喷嚏x建筑工人)
= P(打喷嚏x建筑工人|感冒) x P(感冒)
/ P(打喷嚏x建筑工人)
假定"打喷嚏"和"建筑工人"这两个特征是独立的,因此,上面的等式就变成了
P(感冒|打喷嚏x建筑工人)
= P(打喷嚏|感冒) x P(建筑工人|感冒) x P(感冒)
/ P(打喷嚏) x P(建筑工人)
这是可以计算的。
P(感冒|打喷嚏x建筑工人)
= 0.66 x 0.33 x 0.5 / 0.5 x 0.33
= 0.66
因此,这个打喷嚏的建筑工人,有66%的概率是得了感冒。同理,可以计算这个病人患上过敏或脑震荡的概率。比较这几个概率,就可以知道他最可能得什么病。
这就是贝叶斯分类器的基本方法:在统计资料的基础上,依据找到的一些特征属性,来计算各个类别的概率,找到概率最大的类,从而实现分类。
贝叶斯分类的定义
1、设为一个待分类项,而每个a为x的一个特征属性。
2、有类别集合。
3、计算。
4、求出在X个属性条件下,所有类别的概率,选取概率最大的。则X属于概率最大的类别
,则。
根据贝叶斯定理,要求P(A|B),只要求出P(B|A)即可 .这里Y指A,X指B.把B分解为各个特征属性,求出每个类别的每个特征属性即可,如下
1、找到一个已知分类的待分类项集合,这个集合叫做训练样本集。
2、统计得到在各类别下各个特征属性的条件概率估计。即。
3、如果各个特征属性是条件独立的,则根据贝叶斯定理有如下推导:
因为分母对于所有类别为常数,因为我们只要将分子最大化皆可。又因为各特征属性是条件独立的,所以有:
上式等号右边的每一项,都可以从统计资料中得到,由此就可以计算出每个类别对应的概率,从而找出最大概率的那个类。
注意:各个特征属性是条件独立的,这是朴素贝叶斯所要求的,如果各个特征属性不独立,就不属于朴素贝叶斯,属于贝叶斯网络,后面的文章会讲解。
账号真假检测例子
再看一个例子,该例子来自网上张阳的算法杂货铺博文
根据某社区网站的抽样统计,该站10000个账号中有89%为真实账号(设为C0),11%为虚假账号(设为C1)。
C0 = 0.89
C1 = 0.11
接下来,就要用统计资料判断一个账号的真实性。假定某一个账号有以下三个特征:
F1: 日志数量/注册天数
F2: 好友数量/注册天数
F3: 是否使用真实头像(真实头像为1,非真实头像为0)
F1 = 0.1
F2 = 0.2
F3 = 0
请问该账号是真实账号还是虚假账号?
方法是使用朴素贝叶斯分类器,计算下面这个计算式的值。
P(F1|C)P(F2|C)P(F3|C)P(C)
虽然上面这些值可以从统计资料得到,但是这里有一个问题:F1和F2是连续变量,不适宜按照某个特定值计算概率。
一个技巧是将连续值变为离散值,计算区间的概率。比如将F1分解成[0, 0.05]、(0.05, 0.2)、[0.2, +∞]三个区间,然后计算每个区间的概率。在我们这个例子中,F1等于0.1,落在第二个区间,所以计算的时候,就使用第二个区间的发生概率。
根据统计资料,可得:
P(F1|C0) = 0.5, P(F1|C1) = 0.1
P(F2|C0) = 0.7, P(F2|C1) = 0.2
P(F3|C0) = 0.2, P(F3|C1) = 0.9
因此,
P(F1|C0) P(F2|C0) P(F3|C0) P(C0)
= 0.5 x 0.7 x 0.2 x 0.89
= 0.0623
P(F1|C1) P(F2|C1) P(F3|C1) P(C1)
= 0.1 x 0.2 x 0.9 x 0.11
= 0.00198
可以看到,虽然这个用户没有使用真实头像,但是他是真实账号的概率,比虚假账号高出30多倍,因此判断这个账号为真。
贝叶斯分类的含义
长久以来,人们对一件事情发生或不发生的概率,只有固定的0和1,即要么发生,要么不发生,从来不会去考虑某件事情发生的概率有多大,不发生的概率又是多大。比如如果问那时的人们一个问题:“有一个袋子,里面装着若干个白球和黑球,请问从袋子中取得白球的概率是多少?”他们会想都不用想,会立马告诉你,取出白球的概率就是1/2,要么取到白球,要么取不到白球,即θ只能有一个值,不是1/2,就是0,而且不论你取了多少次,取得白球的概率θ始终都是1/2,即不随观察结果X 的变化而变化。
直到贝叶斯定理的出现,贝叶斯定理不把概率θ看做一个固定的值(比如上面取白球的概率一直都是1/2),而看做一个随机变量,他会随着观察结果变化
贝叶斯及贝叶斯派提出了一个思考问题的固定模式:
先验分布 + 样本信息 后验分布
上述思考模式意味着,新观察到的样本信息将修正人们以前对事物的认知。换言之,在得到新的样本信息之前,人们对的认知是先验分布,在得到新的样本信息后,人们对的认知为。
条件概率公式进行变形,可以得到如下形式:
P(A|B)=P(A) * P(B|A)/P(B)
我们把P(A)称为"先验概率",即在事件B发生之前,事件A发生的概率,在事件B发生之前,它是一个无条件分布,因为A还没有与事件B关联上,他是先验分布。
P(A|B)称为"后验概率"(Posterior probability),即在B事件发生之后,我们对A事件概率的重新评估。P(B|A)/P(B)称为"可能性函数"(Likelyhood),这是一个调整因子,使得预估概率更接近真实概率。它的分布就是后验分布
所以,条件概率可以理解成下面的式子:
后验概率 = 先验概率 x 调整因子
这就是贝叶斯推断的含义。我们先预估一个"先验概率",然后加入实验结果,看这个实验到底是增强还是削弱了"先验概率",由此得到更接近事实的"后验概率"。
在这里,如果"可能性函数"P(B|A)/P(B)>1,意味着"先验概率"被增强,事件A的发生的可能性变大;如果"可能性函数"=1,意味着B事件无助于判断事件A的可能性;如果"可能性函数"<1,意味着"先验概率"被削弱,事件A的可能性变小。
水果糖问题例子
这个例子同样来自阮一峰老师的博文,加深对贝叶斯推断的理解
第一个例子。两个一模一样的碗,一号碗有30颗水果糖和10颗巧克力糖,二号碗有水果糖和巧克力糖各20颗。现在随机选择一个碗,从中摸出一颗糖,发现是水果糖。请问这颗水果糖来自一号碗的概率有多大?
我们假定,H1表示一号碗,H2表示二号碗。由于这两个碗是一样的,所以P(H1)=P(H2),也就是说,在取出水果糖之前,这两个碗被选中的概率相同。因此,P(H1)=0.5,我们把这个概率就叫做"先验概率",即没有做实验之前,来自一号碗的概率是0.5。
再假定,E表示水果糖,所以问题就变成了在已知E的情况下,来自一号碗的概率有多大,即求P(H1|E)。我们把这个概率叫做"后验概率",即在E事件发生之后,对P(H1)的修正。
根据贝叶斯定理,得到
P(H1|E)=P(H1) * P(E|H1)/P(E)
已知,P(H1)等于0.5,P(E|H1)为一号碗中取出水果糖的概率,等于0.75,那么求出P(E)就可以得到答案。根据全概率公式(不懂全概率公式的可以查找相关资料理解),
P(E)=P(E|H1) * P(H1) + P(E|H2)*P(H2)
所以,将数字代入原方程,得到
P(H1|E)=0.5* 0.75/0.625=0.6
这表明,来自一号碗的概率是0.6。也就是说,取出水果糖之后,H1事件的可能性得到了增强。
连续型特征属性和零概率事件处理
上面讲的特征属性值,都是离散的,账号真假检测例子中把连续的转换成区间,每个区间也可以看成离散的,但是如果在不能这样转换的情况下怎么解决?如果特征属性值是不是离散的,而是连续的怎么办?
我们是站在巨人的肩膀上,前人早已经为我们找到了应对之策
当特征属性为连续值时,通常假定其值服从高斯分布(也称正态分布)。即:
而
因此只要计算出训练样本中各个类别中此特征项划分的各均值和标准差,代入上述公式即可得到需要的估计值。(ak为观察到的属性值)
另一个需要讨论的问题就是当P(a|y)=0怎么办,当某个类别下某个特征项划分没有出现时,就是产生这种现象,这会令分类器质量大大降低。为了解决这个问题,引入了拉普拉斯校准,它的思想非常简单,就是对没类别下所有划分(概率为零的)的计数加1,这样如果训练样本集数量充分大时,并不会对结果产生影响,并且解决了上述频率为零的尴尬局面。
买电脑是否和收入相关的例子
验证买电脑,是否和收入有关的场景下:
类 buys_computer=yes包含1000个元组,有0个元组income=low ,990个元组 income=medium,10个元组income=high,这些事件的概率分别是0, 0.990, 0.010.
有概率为0,肯定不行.使用拉普拉斯校准,对每个收入-值对应加1个元组,分别得到如下概率
1/1003=0.001
991/1003=0.998
11/1003=0.011
这些校准的概率估计与对应的未校准的估计很接近,但是避免了零概率值
性别分类的例子
再看一个阮一峰老师的朴素贝叶斯应用一文中摘自维基百科的例子,关于处理连续变量的另一种方法。
下面是一组人类身体特征的统计资料。
性别 身高(英尺) 体重(磅) 脚掌(英寸)
男 6 180 12
男 5.92 190 11
男 5.58 170 12
男 5.92 165 10
女 5 100 6
女 5.5 150 8
女 5.42 130 7
女 5.75 150 9
已知某人身高6英尺、体重130磅,脚掌8英寸,请问该人是男是女?
根据朴素贝叶斯分类器,计算下面这个式子的值。
P(身高|性别) x P(体重|性别) x P(脚掌|性别) x P(性别)
这里的困难在于,由于身高、体重、脚掌都是连续变量,不能采用离散变量的方法计算概率。而且由于样本太少,所以也无法分成区间计算。怎么办?
这时,可以假设男性和女性的身高、体重、脚掌都是正态分布,通过样本计算出均值和方差,也就是得到正态分布的密度函数。有了密度函数,就可以把值代入,算出某一点的密度函数的值。
比如,男性的身高是均值5.855、方差0.035的正态分布。所以,男性的身高为6英尺的概率的相对值等于1.5789(大于1并没有关系,因为这里是密度函数的值,只用来反映各个值的相对可能性)。
有了这些数据以后,就可以计算性别的分类了。
P(身高=6|男) x P(体重=130|男) x P(脚掌=8|男) x P(男)
= 6.1984 x e-9
P(身高=6|女) x P(体重=130|女) x P(脚掌=8|女) x P(女)
= 5.3778 x e-4
可以看到,女性的概率比男性要高出将近10000倍,所以判断该人为女性。






















 4059
4059











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








