【刷题】动态规划专题（二）背包问题

322. 零钱兑换

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。
示例 1:
输入: coins = [1, 2, 5], amount = 11
输出: 3
解释: 11 = 5 + 5 + 1
示例 2:
输入: coins = [2], amount = 3
输出: -1

分析：

1. dp[i]：满足amout为i所需的最少金币数
2. 确定转移方程：
3. 每个dp[i]的值是根据之前的最小硬币数得到的，所以从前往后计算。
4. 对金币按面值从小到大排序，如果amount比最小面值都小，那根本无法凑到，所以小于coins[0]的dp[i]都初始化为-1。
   dp[0]=0

解法一

class Solution {
public:
    
    int coinChange(vector<int>& coins, int amount) {
        vector<int>dp(amount+1);
        sort(coins.begin(),coins.end());
        int n = coins.size();
        for(int i=0;i<=amount;i++){
            if(i<coins[0])
                dp[i] = -1;
        }
        dp[0] = 0;
        for(int i=coins[0];i<=amount;i++){
            int temp = INT_MAX;
            for(int j =0;j<n;j++){
                if(i>=coins[j]&&dp[i-coins[j]]!=-1)
                //当前的amount必须大于硬币面值，不然会越界，当i-coins[j]小于最小面值时无解
                    temp = min(temp,dp[i-coins[j]]);
            }
            if(temp==INT_MAX)
                dp[i] = -1;
            else dp[i] = temp+1;
        }
        return dp[amount];
    }
   
};

解法二
带备忘录的回溯

class Solution {
public:
    int dp[100000];
    int coinChange(vector<int>& coins, int amount) {
        sort(coins.begin(),coins.end());
        if(amount==0)return 0;
        if(amount<coins[0])return -1;
        return dfs(coins,amount);
    }
    int dfs(vector<int>& coins, int amount){
        if(amount<0)return -1;
        if(amount==0) return 0;
        int temp = INT_MAX ;
        if(dp[amount]==0){
            for(int i=0;i<coins.size();i++){
                int v = dfs(coins,amount-coins[i]);
                if(v!=-1)
                    temp = min(temp,v);
            }
            if(temp==INT_MAX)
                dp[amount] = -1;
            else dp[amount] = temp+1;
        }
        return dp[amount];
    }
};

01背包问题

有 n 个物品和一个大小为 m 的背包. 给定数组 A 表示每个物品的大小和数组 V 表示每个物品的价值.
问最多能装入背包的总价值是多大?
样例
样例 1:
输入: m = 10, A = [2, 3, 5, 7], V = [1, 5, 2, 4]
输出: 9
解释: 装入 A[1] 和 A[3] 可以得到最大价值, V[1] + V[3] = 9
样例 2:
输入: m = 10, A = [2, 3, 8], V = [2, 5, 8]
输出: 10
解释: 装入 A[0] 和 A[2] 可以得到最大价值, V[0] + V[2] = 10
挑战
O(nm) 空间复杂度可以通过, 不过你可以尝试 O(m) 空间复杂度吗?
注意事项：
A[i], V[i], n, m 均为整数
你不能将物品进行切分
你所挑选的要装入背包的物品的总大小不能超过 m
每个物品只能取一次

1.dp[i][j]]:从前i个物品中选取一些装到容量为j的背包里，可获得的最大价值（不一定装满）
2.转移方程：

由转移方程可以得到dp[i][j]只和dp[i-1]这一行有关系，所以可以把dp矩阵压缩为一维的，得到转移方程：
dp[j]:容量为j时从当前i个物品中挑选一部分放入背包得到的最大价值。

3.等号左边的dp[j]是当前需要计算的，等号右边的是上一轮计算得到的，如果从前往后计算的话，那前面的dp[j]就会被覆盖掉，所以只能逆序计算，而且j<w[i]的值不变，只需要计算j>=w[i],而且需要计算的dp[j]只依赖于前面的值。
4.初始化：dp[j]=0,任何容量的背包装入0个物品时，最大价值都为0.

class Solution {
public:
    int backPackII(int m, vector<int> &A, vector<int> &V) {
        // write your code here
        vector<int>dp(m+1,0);
        for(int i=0;i<A.size();i++){
            for(int j = m;j>=A[i];j--){
                dp[j] = max(dp[j],dp[j-A[i]]+V[i]);
            }
        }
        int res = 0;
        for(int i=0;i<m+1;i++){
            res = max(res,dp[i]);
        }
        return res;
        
    }
};

完全背包问题
和0/1背包的区别在于，完全背包的物品个数是无限的。也就是一个物品可以放入1件，2件，…，直到超过容量。
转移方程：

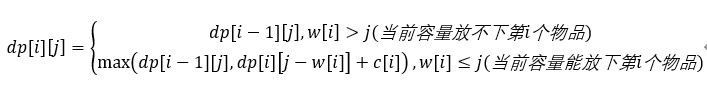
区别在于当可以放下的时候，是dp[i-1][j]和dp[i][j-w[i]]+c[i]比较，也就是即使放了第i件物品后还可以继续放i，只要容量允许。
将dp矩阵进行压缩

方程和0/1背包是一样的，但是计算的顺序不一样从前往后计算，因为完全背包用的是第i行的新数据进行比较。
参考：视频讲解

class Solution {
public:
    int backPackII(int m, vector<int> &A, vector<int> &V) {
        // write your code here
        vector<int>dp(m+1,0);
        for(int i=0;i<A.size();i++){
            for(int j = A[i];j<=m;j++){
                dp[j] = max(dp[j],dp[j-A[i]]+V[i]);
            }
        }
        int res = 0;
        for(int i=0;i<m+1;i++){
            res = max(res,dp[i]);
        }
        return res;
        
    }
};

背包问题
中文English
在n个物品中挑选若干物品装入背包，最多能装多满？假设背包的大小为m，每个物品的大小为A[i]
样例
样例 1:
输入: [3,4,8,5], backpack size=10
输出: 9
样例 2:
输入: [2,3,5,7], backpack size=12
输出: 12
挑战
O(n x m) 的时间复杂度 and O(m) 空间复杂度
如果不知道如何优化空间O(n x m) 的空间复杂度也可以通过.
注意事项
你不可以将物品进行切割。

这个问题和0/1背包问题的区别是，物品的价值变成了它自身的大小，也就是直接将+c[i]改成+w[i]即可。

class Solution {
public:
    /**
     * @param m: An integer m denotes the size of a backpack
     * @param A: Given n items with size A[i]
     * @return: The maximum size
     */
    int backPack(int m, vector<int> &A) {
        // write your code here
        vector<int>dp(m+1,0);//dp[i]:容量为i时能装下的物品的最大体积
        int res= 0;
        for(int i =0;i<A.size();i++){
            for(int j=m;j>=A[i];j--){
                dp[j] = max(dp[j],dp[j-A[i]]+A[i]);
                res = max(res,dp[j]); 
            }
        }
        return res;
    }
};

518. 零钱兑换 II

给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。
示例 1:
输入: amount = 5, coins = [1, 2, 5]
输出: 4
解释: 有四种方式可以凑成总金额:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
示例 2:
输入: amount = 3, coins = [2]
输出: 0
解释: 只用面额2的硬币不能凑成总金额3。
示例 3:
输入: amount = 10, coins = [10]
输出: 1
注意:
你可以假设：
0 <= amount (总金额) <= 5000
1 <= coin (硬币面额) <= 5000
硬币种类不超过 500 种
结果符合 32 位符号整数

这个题和爬楼梯那道题是不同的，子问题是有重叠的。
比如示例1中，如果dp[i]表示总面额为i时的方案数，那dp[5]=dp[5-1]+dp[5-2]+dp[5-5]
=dp[4]+dp[3]+dp[0]
dp[4] 有三种方案：
1+1+1+1
2+1+1
2+2
dp[3]有两种方案：
1+1+1
2+1
凑dp[5]时，就相当于在此基础上加硬币的面值，但是dp[4]最后一种方案，对应的是2+2+1,dp[3]最后一种方案，对应的是2+1+2,它们实质上是一种，重复计算了，所以这种思路是错误的。
换一种思路
1.dp[i][j]:从前i种硬币种挑选凑成金额j的方案数。
2.转移方程：从前i种硬币种挑选凑成金额j的方案数=不用第i种硬币就凑得金额的方案数+用第i种硬币凑得金额的方案数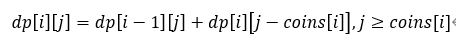
可以看成是一个完全背包的变形。
将dp矩阵进行压缩得到

class Solution {
public:
    int change(int amount, vector<int>& coins) {
        vector<int>dp(amount+1,0);
        dp[0]=1;
        for(int i=0;i<coins.size();i++){
            for(int j = coins[i];j<=amount;j++){
                dp[j] += dp[j-coins[i]];
            }
        }
        return dp[amount];
    }
};

同类题目：562. 背包问题 IV