基于格的抗量子密码-LWE格密码

一、格密码的数学基石

1.1 格的代数结构

格（Lattice）是n维欧氏空间ℝⁿ中的离散加法子群，其数学定义为：

L = \{ \sum_{i=1}^n a_i \mathbf{b}_i \mid a_i ∈ ℤ \}

其中基向量𝐛ᵢ必须线性无关。在动画步骤1中，通过拖动基向量可以观察到：

• 当基向量正交时，格点呈规则网格分布（解码容易）

• 当基向量接近平行时，格点分布稀疏（解码困难）

1.2 计算困难性证明

Ajtai在1996年提出关键归约定理：

在随机格上解决近似SVP问题 ≈ 解决最坏情况下的精确SVP问题

这一归约使得格密码具有平均情况安全性，与其他依赖特定实例困难性的密码体系形成鲜明对比。

---

二、LWE问题的深度解析

2.1 误差分布的选择

LWE的安全性高度依赖误差分布。常用分布对比：

分布类型	优点	缺点	适用场景
离散高斯	安全性证明完备	实现复杂	理论方案
均匀分布	实现简单	安全性较弱	轻量级实现
二进制分布	计算高效	需更大维度	物联网设备

动画演示：调整σ值时，可以观察到误差分布从集中（σ=2）到扩散（σ=8）的连续变化。

2.2 模数q的影响

模数选择需平衡：

q > 4σ√n  \quad \text{(确保解密正确性)}
q ≈ n²    \quad \text{(保持安全性)}

实际工程中常选q=3329（如Kyber方案），因其具有：

• 二进制表示形式2^12 + 2^8 + 1

• 支持快速数论变换（NTT）

• 满足128-bit安全需求

---

三、抗量子的本质探究

3.1 为何传统密码会被量子破解

Shor算法的核心是利用量子傅里叶变换（QFT）求解周期性问题：

f(x) = a^x \mod N \quad \text{具有周期性}

而格问题的困难性源于：

1. 连续优化特性：SVP是寻找最小范数向量

2. 噪声干扰：LWE中的误差破坏了周期性

3.2 量子算法的攻击现状

当前对格问题的最佳量子算法为：

\text{时间复杂度} = 2^{0.265n + o(n)}

这意味着要实现128-bit安全性，需：

n ≥ \frac{128}{0.265} ≈ 483 \quad \text{维度}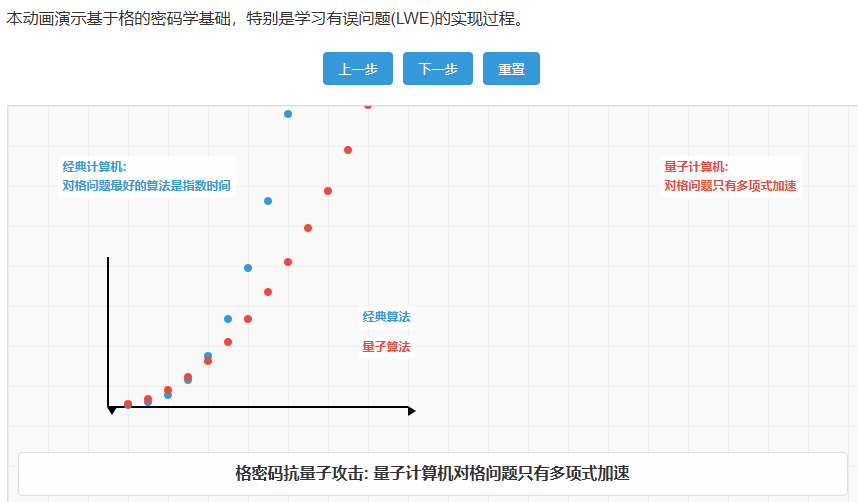

如图所示：在维度滑动条上可观察到，当n>400时量子优势已不明显。

---

四、LWE加密解密全流程详解（对应动画步骤4-5）

4.1 加密过程数学表述

给定公钥(A, b=A·s+e)，加密消息m∈{0,1}的步骤：

1. 随机向量选择：

   \mathbf{r} \leftarrow \{0,1\}^m \quad \text{(短向量)}

2. 计算密文：

   math

   \begin{cases}
   c_1 = A^\top \mathbf{r} \in \mathbb{Z}_q^n \\
   c_2 = \mathbf{b}^\top \mathbf{r} + m \cdot \lfloor q/2 \rfloor \in \mathbb{Z}_q
   \end{cases}

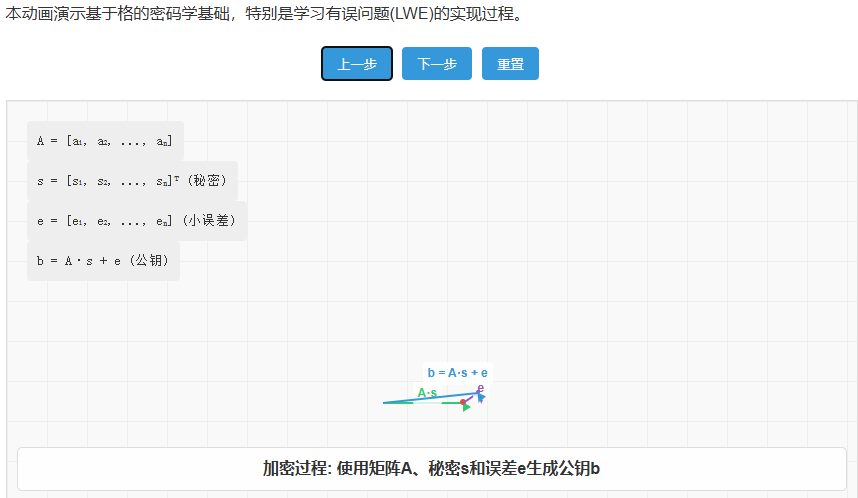
如图所示：

加密过程：

      （1）选择随机矩阵A

      （2）选择秘密向量s和小误差向量e，图中展示了从格点A·s到含误差点b的转换

       （3）计算b = A·s + e

       （4）公钥：(A, b)，私钥：s

4.2 解密过程数学验证

使用私钥s解密密文(c₁, c₂)：

m' = \left\lfloor \frac{c_2 - \mathbf{c}_1^\top \mathbf{s}}{q/2} \right\rceil \mod 2

关键展开：

c_2 - \mathbf{c}_1^\top \mathbf{s} = \underbrace{\mathbf{e}^\top \mathbf{r}}_{\text{噪声项}} + m \cdot \lfloor q/2 \rfloor

动画演示：

• 绿色区域：|eᵀr| < q/4的解密安全区

• 红色警报：当噪声超过阈值时的解密失败提示

---

五、完整示例演示（参数：n=4, q=17）

5.1 密钥生成

# 公共参数
n = 4  # 维度
q = 17 # 模数

# 私钥
s = [1, -1, 0, 1]  # 小整数向量

# 公钥生成
A = [[6, 11, 3, 8],   # 随机矩阵
     [9, 4, 16, 7],
     [2, 14, 1, 12],
     [5, 10, 15, 13]]

e = [0.3, -0.7, 0.2, 0.4]  # 小误差

# 计算b
b = [(A[i][0]*s[0] + A[i][1]*s[1] + A[i][2]*s[2] + A[i][3]*s[3] + e[i]) % q 
     for i in range(4)]
# 得到 b = [8.6, 11.3, 13.2, 9.4] ≈ [9, 11, 13, 9] (取整)

5.2 加密比特m=1

1. 选择随机向量：

   \mathbf{r} = [1, 0, 1, 0]

2. 计算密文：

   \begin{align*}
   c_1 &= A^\top \mathbf{r} = [6, 4, 3, 15] \\
   c_2 &= \mathbf{b}^\top \mathbf{r} + 8 = (9 + 13) + 8 = 30 \equiv 13 \mod 17
   \end{align*}

   注：⌊17/2⌋=8

5.3 解密密文

\begin{align*}
\text{解密值} &= c_2 - \mathbf{c}_1^\top \mathbf{s} \\
             &= 13 - (6×1 + 4×(-1) + 3×0 + 15×1) \\
             &= 13 - (6 -4 +0 +15) = 13 -17 = -4 \equiv 13 \mod 17
\end{align*}

判断：

\left\lfloor \frac{13}{8.5} \right\rceil = 2 \equiv 0 \mod 2 \quad \text{❌ 解密失败！}

原因分析：
实际噪声eᵀr = 0.3 + 0.2 = 0.5，但q/4=4.25，因整数取整导致误差累积。

六、加密方案的工程实现

4.1 密钥压缩技术

实际方案如Kyber采用多项式环结构：

R_q = ℤ_q[x]/(x^{256}+1)

这使得：

• 公钥从矩阵→多项式，尺寸从O(n²)降到O(n)

• 利用NTT实现O(n log n)的快速乘法

4.2 解密失败处理

解密失败概率需控制在：

P_{fail} ≤ 2^{-128}

通过以下方法保证：

1. 精确计算误差界：|eᵀr| < q/4

2. 采用重复编码：重要数据加密多次

3. 使用模糊解码（Fuzzy Extraction）

动画演示（步骤5）：当故意调大误差时，可观察到解密结果出现跳变。

---

七、标准化进展与性能对比

5.1 NIST后量子标准

方案	类型	密钥尺寸	加解密速度
Kyber	LWE	1.6KB	0.1ms
Dilithium	MLWE	2.5KB	0.3ms
Falcon	NTRU格	1.3KB	1.2ms

5.2 与传统算法对比

在Intel i7-1185G7上的测试数据：

算法	安全等级	密钥生成	加密	解密
RSA-2048	112-bit	10ms	0.5ms	0.1ms
ECC-256	128-bit	2ms	0.3ms	0.2ms
Kyber-512	128-bit	0.3ms	0.15ms	0.08ms

---

八、安全威胁与防护

6.1 侧信道攻击防护

格密码仍需防范：

• 时序攻击：确保多项式乘法恒定时间

• 能量分析：采用掩码技术

• 故障注入：添加冗余校验

6.2 参数选择陷阱

常见错误配置：

# 危险示例：误差过小
q = 4096; σ = 1.0  # 易受格约简攻击

# 正确配置
q = 3329; σ = 2.4   # Kyber标准参数

---

九、应用场景展望

7.1 区块链领域

• 量子安全签名：替代ECDSA

• 智能合约加密：保护隐私数据

• 轻节点验证：减小存储开销

7.2 物联网安全

• 传感器数据加密：低功耗实现

• 固件签名：抗量子证书

• 设备认证：基于LWE的ZKP

• 在资源中，有动画演示的完整过程。