【OpenCV】OpenCV傅里叶变换基础知识

一、基础概念

参考1：https://blog.csdn.net/on2way/article/details/46981825
参考知乎大佬：https://zhuanlan.zhihu.com/p/19763358

1.1 频域基础概念

1.1.1 频谱（频域图像，正弦波振幅）

  频域图像又称频谱。时域到频域的变换，从侧面可以看到频谱，这个频谱并没有包含时域中全部的信息，只代表每一个对应的正弦波的振幅。
    
    
    

1.1.2 相位谱(正弦波相位)

  频谱只代表每一个对应的正弦波的振幅是多少。基础的正弦波A.sin(wt+θ)中，振幅，频率，相位缺一不可，不同相位决定了波的位置，所以对于频域分析，仅仅有频谱（振幅谱）是不够的，还需要一个相位谱。
        
          
  时间差： 距离频率轴最近的波峰，而这个波峰所处的位置离频率轴的距离为时间差。
  相位差： 时间差并不是相位差，相位差是时间差在一个正弦波周期中所占的比例。我们将时间差除周期再乘2Pi，就得到了相位差。
  相位谱： 所有正弦波的相位差，构成的图像。频谱是从侧面看，相位谱是从下面看。
        

1.1.3 频率

  正弦波周期

1.2 傅里叶变换

1.2.1 概念

离散频谱和连续频谱

  傅里叶级数的本质是将一个周期的信号分解成无限多分开的（离散的）正弦波。

          
  ①傅里叶级数：在时域是一个周期且连续的函数，而在频域是一个非周期离散的函数
  ②傅里叶变换：将一个时域非周期的连续信号，转换为一个在频域非周期的连续信号。换一个角度理解：傅里叶变换实际上是对一个周期无限大的函数进行傅里叶变换。
  离散频谱：
  正弦波是离散的，相聚很远
        
  连续频谱：
  离散的正弦波离得越来越近，逐渐变得连续。离散谱的叠加，变成了连续谱的累积。所以在计算上也从求和符号变成了积分符号。

复数

  虚数i是-1的平方根，既i**2=-1。
  例：数轴上红色的线段，当它乘以-1的时候，就变成了绿色的线段，线段在数轴上围绕原点旋转了180度。乘-1其实就是乘了两次 i使线段旋转了180度，那么乘一次 i 就是旋转了90度。

      
        
  实数轴与虚数轴共同构成了一个复数的平面，也称复平面。乘虚数i的一个功能——旋转。

欧拉公式

        
  公式关键的作用，是将正弦波统一成了简单的指数形式。
        
  欧拉公式所描绘的，是一个随着时间变化，在复平面上做圆周运动的点，随着时间的改变，在时间轴上就成了一条螺旋线。实数部分（螺旋线在左侧的投影）是一个最基础的余弦函数。虚数部分（螺旋线在右侧的投影）是一个正弦函数。
  欧拉公式告诉我们：余弦波的叠加，也可以理解为螺旋线的叠加在实数空间的投影。
  两种方法理解正弦波：
  （1）螺旋波在实数轴的投影
  （2）根据欧拉公式的另一种形式去理解
        
  将以上两式相加除以2
        
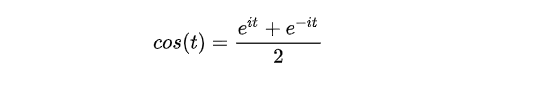
  e^(it)可以理解为一条逆时针旋转的螺旋线，那么e^(-it)则可以理解为一条顺时针旋转的螺旋线。而cos(t)则是这两条旋转方向不同的螺旋线叠加的一半。因为这两条螺旋线的虚数部分相互抵消掉了
  连续的傅里叶变换频谱（下图）：连续的傅里叶变换频谱上的每一条螺旋线都是可以清楚的看到的，每一条螺旋线都有着不同的振幅（旋转半径），频率（旋转周期）以及相位。而将所有螺旋线连成平面，得到这幅连续的傅里叶变换频谱
        
  图形在时域的样子
    

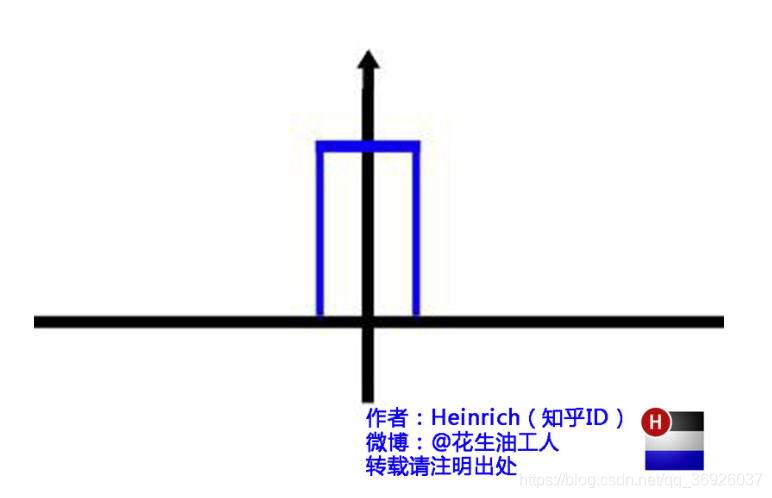
1.2.2 傅里叶变换

  傅里叶变换：就是将一副图片分解为正弦和余弦两个分量，以完成一幅图像从空间域转换为频域。这种变换的思想是任何函数可以很精确的接近无穷个sin()函数和cos()函数的和。
  时域图像转换到频域时是以复数的形式存在，变换后的结果需要使用实数图像和虚数图像，或幅度图像加相位图像的形式。但在实际处理中仅仅使用了幅度图像，因为幅度图像几乎包含了原图像的几何信息。
  想要使用傅里叶逆变换就需要同时保留幅度图像和相位图像，才能实现对原图像的操作。
  空间域： 空间域的图像是f(x, y) = 灰度级（0-255），形象一点就是一个二维矩阵，每一个坐标对应一个颜色值。
  频率域：
  对于一个正弦信号，如果它的幅度变化很快，我们称之为高频信号，如果变化非常慢，我们称之为低频信号。迁移到图像中，图像哪里的幅度变化非常大呢？边界点或者噪声。所以我们说边界和噪声是图像中的高频分量（这里的高频是指变化非常快，不是出现的次数多），图像的主要部分（图像的、纹理信息）集中在低频分量。因此傅里叶变换在图像处理中可以做到图像增强和去噪、图像分割之边缘检测、图像特征提取和压缩等。
                  
  式中 f(i, j)是图像空间域的值，F(k ,l)是频域的值。傅里叶转换的结果是复数，这也显示了傅里叶变换是一幅实数图像和虚数图像叠加或者是幅度图像和相位图像叠加的结果。