《Bayesian Persuation》,是经济学理论研究的一篇经典论文,2011年发表在AER上。
目录
1. Motivation: 起诉人和法官博弈
首先,看一个起诉人和法官博弈的案例。
起诉人的目的是让理性的法官相信他是有罪的。法官有两个行动选择:定罪或无罪释放。对于被告来说,他的真实状态要么是有罪的,要么是无辜的。对于起诉人来说,如果被告被定罪,效用为1,否则为0。对于法官来说,判对了效用为1,判错为0。起诉人和法官共有一个先验信念:Pr(guilty)=0.3,也就是被告有罪的概率为30%。
起诉人可以调查搜集证据pi,并且必须把所有调查结果如实向法庭报告。但是起诉人可以选择调查方式和调查内容。考虑两种极端情况,如果不调查,也就是pi中不包含任何信息,那么法官基于先验0.3会判定被告无罪;如果调查了所有事实真相,也就是pi包含完全的信息,那么法官基于调查出来的事实,有0.3的概率判有罪,0.7的概率判无罪。如果起诉人选择下面一种调查方式:
π ( i ∣ i n n o c e n t ) = 4 / 7 \pi(i|innocent)=4/7 π(i∣innocent)=4/7, π ( i ∣ g u i t y ) = 0 \pi(i|guity)=0 π(i∣guity)=0,
π ( g ∣ i n n o c e n t ) = 3 / 7 \pi(g|innocent)=3/7 π(g∣innocent)=3/7, π ( g ∣ g u i t y ) = 1 \pi(g|guity)=1 π(g∣guity)=1.
注: P r ( i n n o c e n t ) = 0.7 Pr(innocent)=0.7 Pr(innocent)=0.7, P r ( g u i l t y ) = 0.3 Pr(guilty)=0.3 Pr(guilty)=0.3,
被告被判有罪的概率 = π ( g ∣ i n n o c e n t ) P r ( i n n o c e n t ) + π ( g ∣ g u i l t y ) P r ( g u i l t y ) = 3 / 7 ∗ 0.7 + 1 ∗ 0.3 = 0.6 =\pi(g|innocent)Pr(innocent)+\pi(g|guilty)Pr(guilty)=3/7*0.7+1*0.3 =0.6 =π(g∣innocent)Pr(innocent)+π(g∣guilty)Pr(guilty)=3/7∗0.7+1∗0.3=0.6
之前法官相信被告70%是无辜的,但是最后他有60%的可能性判他有罪。虽然法官也知道起诉人的调查最大化了被告被判有罪的概率,但是他也没有办法。
现在假定如下一个法庭案例:起诉人(prosecutor)尝试劝说法官(judge)使之相信被告人(defendant)是有罪的。当被告人的确是有罪的,那么越揭露事实的真相越对起诉人有利;但如果被告人是无辜的,那么揭露事实真相对起诉人是不利的。那么问题来了:起诉人是否可以通过组织其论据,比如选择证据,来增加理性的法官判决被告人有罪的概率?结果也许很惊喜:Yes!贝叶斯定理限定了后验信念的期望(expectation),但是并未限制其分布(distribution),因此,只要法官的行动与其信念不是线性的关系,起诉人就可以通过劝说(persuasion)来获益。
2. Problem: 该不该劝说以及如何劝说?
那么问题来了,假如现在有一个人Sender试图劝说另一个人Receiver改变她的行动。如果 Receiver是一个理性的人,并且如果清楚Sender是在通过选择信息来操纵她的行动。那么Sender可以从劝说中获得好处吗?如果可以,需要满足什么条件吗?最优的劝说方式是怎样的?
这个问题很有价值,因为劝说问题存于很多领域,比如广告营销、法庭辩护、财务披露、政治选举等。
3. Model
考虑一个信息对称的模型,有两个player,一个信息的发送者sender和一个接收者receiver. Receiver和Sender的效用函数分别是u(a,w)和v(a,w),a是行动,w是state of world。双方有共同的先验miu0。
- 首先,Sender向receiver发出一个signal π \pi π,本质是一组条件概率,given S, 在 ω \omega ω时不同的s有不同的概率,组成了一个signal。
- 然后receiver观察到signal后,贝叶斯更新自己的belief μ s \mu_s μs,并采取一个最大化自己期望效用的行动。Sender可以预测Receiver的对应行动,所以会选择一个最优的signal π \pi π来最大化自己的期望收益。
本质是一个子博弈精炼纳什均衡。
(1)如何根据s更新 μ s ( ω ) \mu_s(\omega) μs(ω)?
μ s ( ω ) = μ ( ω ∣ s ) \mu_s (\omega)=\mu(\omega|s) μs(ω)=μ(ω∣s)即s时 ω \omega ω的概率。

(2)一组 μ ( ω ∣ s ) \mu(\omega|s) μ(ω∣s)构成了后验分布, τ \tau τ则表示后验分布 μ ′ \mu' μ′的概率, τ ( μ ) \tau(\mu) τ(μ)则表示后验分布 μ \mu μ的概率。
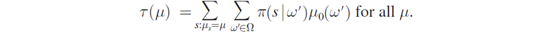
后面的求和项 = π ( s ) =\pi(s) =π(s)( π








 《Bayesian Persuasion》论文探讨了在信息不对称情况下,如何通过选择性地传递信息来影响他人的决策。通过起诉人与法官博弈的案例,展示了起诉人如何通过策略性劝说增加法官判被告有罪的概率。文章分析了是否应进行劝说、如何劝说以及最优劝说方式,应用到现实场景如产品信息提供,揭示了商业中市场细分战略的说服力和可信度建立的重要性。
《Bayesian Persuasion》论文探讨了在信息不对称情况下,如何通过选择性地传递信息来影响他人的决策。通过起诉人与法官博弈的案例,展示了起诉人如何通过策略性劝说增加法官判被告有罪的概率。文章分析了是否应进行劝说、如何劝说以及最优劝说方式,应用到现实场景如产品信息提供,揭示了商业中市场细分战略的说服力和可信度建立的重要性。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1305
1305

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








