COMP3023 Design and Analysis of Algorithms

 一个学生作业，拿去吧，直接用

package com.xxl.job.executor.service.jobhandler;

import java.io.*;
import java.util.*;

public class DAG {
    public static void main(String[] args) throws IOException {
        // 读取输入文件 in.txt
        String inputInFile = "C:\\Users\\Administrator\\Desktop\\in.txt";
        BufferedReader reader = new BufferedReader(new FileReader(inputInFile));
        int fileN = Integer.parseInt(reader.readLine().trim());
        int[] uvs = Arrays.stream(reader.readLine().split("\\s+"))
                .mapToInt(Integer::parseInt).toArray();
        int u = uvs[0], v = uvs[1];
        int[] weights = Arrays.stream(reader.readLine().split("\\s+"))
                .mapToInt(Integer::parseInt).toArray();
        // 读取邻接矩阵并构建邻接表
        List<List<Integer>> listArrayList = new ArrayList<>();
        for (int i = 0; i < fileN; i++) {
            listArrayList.add(new ArrayList<>());
            int[] rows = Arrays.stream(reader.readLine().split("\\s+"))
                    .mapToInt(Integer::parseInt).toArray();
            for (int j = 0; j < fileN; j++) {
                if (rows[j] == 1) listArrayList.get(i).add(j);
            }
        }
        reader.close();
        // 拓扑排序
        List<Integer> topOrders = kahnTopoLogicalSort(listArrayList, fileN);
        // 动态规划计算最大路径
        long[] dps = new long[fileN];
        Arrays.fill(dps, Long.MIN_VALUE);
        dps[u] = weights[u];
        int[] prev = new int[fileN];
        Arrays.fill(prev, -1);
        for (int node : topOrders) {
            if (dps[node] == Long.MIN_VALUE) continue;
            for (int neighbor : listArrayList.get(node)) {
                if (dps[neighbor] < dps[node] + weights[neighbor]) {
                    dps[neighbor] = dps[node] + weights[neighbor];
                    prev[neighbor] = node;
                }
            }
        }
        // 输出结果到out.txt文件中
        String outputToOutFile = "C:\\Users\\Administrator\\Desktop\\out.txt";
        BufferedWriter writer = new BufferedWriter(new FileWriter(outputToOutFile));
        if (dps[v] == Long.MIN_VALUE) {
            writer.write("路径不存在,请检查后处理");
        } else {
            writer.write(dps[v] + "\n");
            List<Integer> paths = reconstructPath(prev, u, v);
            for (int i = 0; i < paths.size(); i++) {
                writer.write(paths.get(i) + (i < paths.size()-1 ? " " : ""));
            }
        }
        writer.close();
    }

    // Kahn算法 -- 拓扑排序
    private static List<Integer> kahnTopoLogicalSort(List<List<Integer>> intersection, int n) {
        // 初始化所有节点的入度数组，用于后续的拓扑排序
        int[] degrees = new int[n];
        // 遍历邻接表，统计每个节点的入度
        for (List<Integer> list : intersection) {
            for (int node : list) {
                degrees[node]++;
            }
        }
        // 使用队列来存储所有入度为0的节点，作为拓扑排序的起始节点
        Queue<Integer> q = new LinkedList<>();
        // 将所有入度为0的节点添加到队列中
        for (int i = 0; i < n; i++) {
            if (degrees[i] == 0) {
                q.add(i);
            }
        }
        // 用于存储拓扑排序结果的列表
        List<Integer> order = new ArrayList<>();
        // 当队列不为空时，进行拓扑排序
        while (!q.isEmpty()) {
            // 从队列中取出一个节点
            int u = q.poll();
            // 将该节点添加到拓扑排序结果中
            order.add(u);
            // 遍历该节点的所有邻接节点，并减少它们的入度
            for (int v : intersection.get(u)) {
                // 如果节点的入度减为0，则将其添加到队列中
                if (--degrees[v] == 0) {
                    q.add(v);
                }
            }
        }
        // 返回拓扑排序结果
        return order;
    }
    private static List<Integer> reconstructPath(int[] prev, int u, int v) {
        // 创建一个列表用于存储从起点到终点的路径
        List<Integer> paths = new ArrayList<>();
        // 从终点v开始，通过prev数组回溯到起点，将路径中的顶点添加到path列表中
        for (int i = v; i != -1; i = prev[i]) {
            paths.add(i);
        }
        // 将路径反转，以便从起点到终点表示路径
        Collections.reverse(paths);
        // 如果路径的起点是u，则返回这条路径；否则返回空列表，表示没有找到有效的路径
        return paths.get(0) == u ? paths : Collections.emptyList();
    }
}

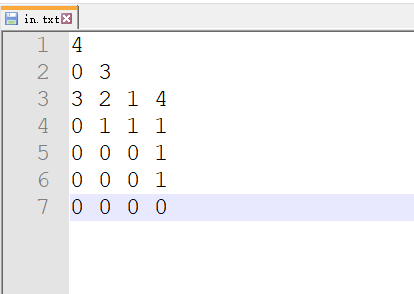
 in.txt文件内容

4
0 3
3 2 1 4
0 1 1 1
0 0 0 1
0 0 0 1
0 0 0 0

 （大环境真可怕，自己卷自己）