大家好,我是北海。
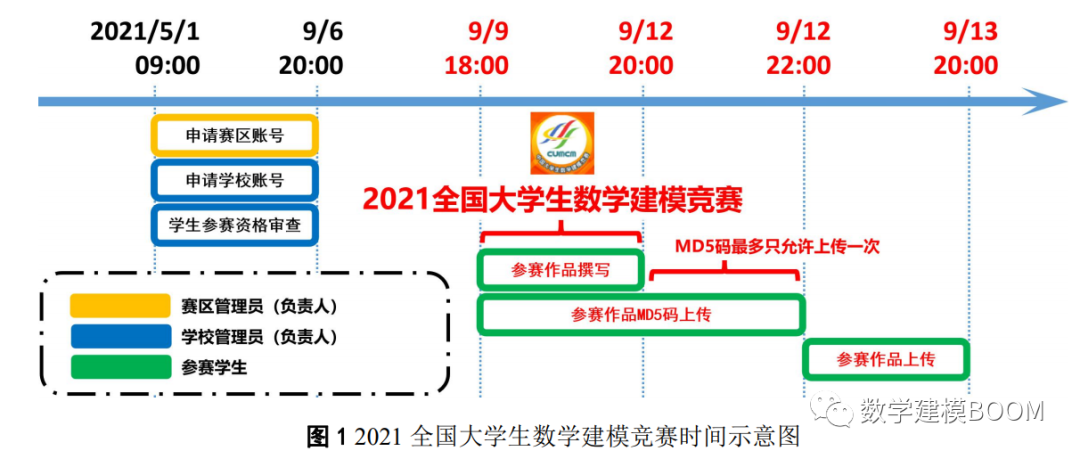
数学建模国赛将于9月6日开赛,本文主要介绍国赛报名与组队安排、赛题知识点趋势,并强调近些年竞赛的一个常见错误操作:滥用启发式算法。

报名与组队
报名
一般院校是学校组织统一报名,如果还未报名的话,联系数学建模社团或数学专业的老师询问,尽快报名。
组队
数学建模是团队竞赛,三天时间交论文,单靠一个人的精力是顶不住的(大佬除外)。因此赛前选择好队友是重中之重。
队友选择
有时看到群友吐槽和讨论队友,基本都是能力和态度方面:
-
能力:选择和自己能力相近的队友,可以在其他竞赛群(例如大创等)招收队友。或者室友、同学有态度靠谱的也可以。
-
态度:三个臭皮匠顶个诸葛亮,什么都不会不要紧,只要态度端正,竞赛期间不怕累,现学现用,照样能取得好成绩。最怕那种一看题目难就跑路、三天找不到人的队友。
任务分配
三人无需明确分工,但也要各自有所侧重。
常见的一人专门建模、一人专门编程和一人专门写论文的安排是大错特错的!
以下分别以“建模者”“编程者”“写作者”称呼侧重负责对应方面的队员。
建模:三人一起讨论模型思路,确保每人都能明白模型架构与原理;参数处理、模型改进与优化等细节交给建模者处理。
编程:模型建立好后,编程者写程序求解问题,如果用到某些算法,需要与另外两人讨论清楚,确保三人思路在一条线,尤其确保写论文的人能理解算法原理。
写论文:涉及模型和算法方面的,要由最能理解模型或算法的人写出梗概交给写作者,由写作者扩充出正文,确保全文语句和排版的风格一致。
而且比赛过程中,三人的任务不是固定的,例如A擅长第一问的模型和第二问的编程,那么就要随时调整每个人侧重的任务。
还需注意,一切工作以论文为中心。因为最终评委看到的就是论文。
处理分歧
如果对于某一问,意见不同该怎么办?
若两个人意见有分歧,那就三个人投票,少数服从多数;
若三个人分别有各自意见,就每个人详细讲述自己的思路,耐心听别人的意见,一定不要吵起来。实在不行抓阄,总比僵持在某一步浪费时间要好。
队友实在不靠谱怎么办
这中情况在头几次参赛很常见。尽量自己一个人坚持做完吧,也算积累经验了,下次组队换队友就是了。
只有多参赛几次,遇到不靠谱的队友下次就不找他,才会有长期稳定的靠谱队伍。可以说遇到坑队友也是必经之路吧!
近10年赛题规律
以下是近10年赛题知识点(本科组)思维导图

赛题趋势
数学建模题目可以分为四类:
-
评价类(最简单)
-
优化类(最常见)
-
预测类
-
机理分析类(人口模型/物理学/微分方程等)
近几年在各项数模赛事中,优化类和机理分析类问题出现的频率显著增高。
1、主要由于近些年竞赛越来越卷,需要提高难度以保持区分度;而评价类和预测类问题有成熟的固定模型可以套用,较为简单;
2、优化类和机理分析类问题则常常涉及交叉学科知识,没有现成模型可以套用,或者有模型但模型或参数需要根据题目改进后才能用,所以更能检验参赛者的实力。
3、但评价类和预测类问题也常常作为某小问或者某一步来出题,因此也不可忽视这两类问题。
慎用启发式算法
包括模拟神经网络、退火算法、遗传算法、蚁群算法等等,这些方法在近些年的数学建模竞赛中出现严重的滥用问题。
启发式算法是在无法直接求出严格最优解的情况下,去求一个近似的可行解。(详细内容可以去看数据结构与算法的书籍中的NP-hard问题和启发式算法)。
举个不科学但形象的例子:计算1+1= ?
-
正常做法:由数学公理可知,结果为2。
-
舍本逐末:由蚁群算法优化BP神经网络回归预测的算法设计求得近似解为1.9985。
很多同学觉得神经网络/蚁群算法等听起来挺新鲜,看起来挺复杂的,用起来似乎很有b格,于是不管什么情况都建立个神经网络模型。
但是如果问题本身就有方法求出严格的数值解,那么用启发式算法就是舍本逐末了。
比如求一些最短路径问题,消防站如何设置能使得尽快救援等等,完全可以用Dijkstra算法、Bellman-Ford算法、Floyd算法等;
而涉及最小生成树问题又有Prime算法、Kruskal算法等,这些在常见的数学建模资料中都可以找到。
如果做这种有严格数值解的题还去使用启发式算法,就基本与获奖无缘了。
有些评审老师很烦动不动就建个神经网络的论文,所以一定要注意,如果问题有好模型和算法的话,就不要用启发式算法。
当然也不是完全不能用,还是要根据实际情况来,错误做法是不分情况的滥用。

总之,找好靠谱队友,竞赛期间合理分配任务,根据近十年国赛知识点趋势有所侧重地学习,再注意避开滥用启发式算法这一误区,国赛定能取得好成绩!























 1253
1253











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










