泊松分布:
历史上泊松分布式作为二项分布的近似，由法国数学家泊松引入。在实际中许多现象都服从泊松分布。从意义上说解决的问题是：“在特定时间内发生n个事件的概率”
泊松分布满足如下公式：
P ( N ( t ) = n ) = ( λ t ) n e − λ t n ! P(N(t) = n) = { ( \lambda t)^ne^{-\lambda t} \over n!} P(N(t)=n)=n!(λt)ne−λt
等号左边P表示概率、N表示事件符合的函数关系、t表示为事件、n为数量、 λ \lambda λ表示为频率。
举例：接下来两个小时，一个婴儿都不出生的概率
P ( N ( 2 ) = 0 ) = ( 3 × 2 ) 0 e − 3 × 2 0 ! ≈ 0.25 P(N(2) = 0) = {(3 \times 2)^0e^{-3 \times 2} \over 0!} \approx 0.25 P(N(2)=0)=0!(3×2)0e−3×2≈0.25
接下来一个小时，至少出生两个婴儿的概率
P ( N ( 1 ) ≥ 2 ) = 1 − P ( N ( 1 ) = 1 ) − P ( N ( 1 ) = 0 ) = 1 − ( 3 × 1 ) 1 e − 3 × 1 1 ! − ( 3 × 1 ) 0 e − 3 × 1 0 ! = 1 − 3 e − 3 − e − 3 = 1 − 4 e − 3 ≈ 0.8009 \begin{array}{l} P(N(1) \geq 2) = 1-P(N(1)=1)-P(N(1)=0) \\ \quad \quad \quad \quad \quad \quad = 1-{(3 \times 1)^1e^{-3 \times 1} \over 1!}-{(3 \times 1)^0e^{-3 \times 1} \over 0!} \\ \quad \quad \quad \quad \quad \quad = 1-3e^{-3}-e^{-3} \\ \quad \quad \quad \quad \quad \quad =1-4e^{-3} \\ \quad \quad \quad \quad \quad \quad \approx 0.8009 \end{array} P(N(1)≥2)=1−P(N(1)=1)−P(N(1)=0)=1−1!(3×1)1e−3×1−0!(3×1)0e−3×1=1−3e−3−e−3=1−4e−3≈0.8009
泊松分布的图形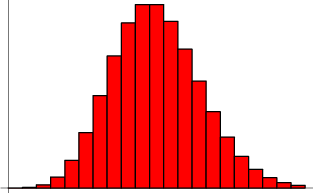
可以看到，在频率附近，事件的发生概率最高，然后向两边对称下降，即变得越大和越小都不太可能。每小时出生3个婴儿，这是最可能的结果，出生得越多或越少，就越不可能。
泊松分布产生的一般条件：
在自然界和人们的现实生活中,经常要遇到在随机时刻出现的某种事件.我们把在随机时刻相继出现的事件所形成的序列,叫做随机事件流。若事件流具有平稳性、无后效性、普通性，则称该事件流为泊松事件流（泊松流）
- 平稳性：在任意时间区间内，事件发生k次(k≥0)的概率只依赖于区间长度而与区间端点无关.
- 无后效性：在不相重叠的时间段内，事件的发生是相互独立的.
- 普通型：如果时间区间充分小，事件出现两次或两次以上的概率可忽略不计.
3万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
