视觉SLAM理论到实践系列文章
下面是《视觉SLAM十四讲》学习笔记的系列记录的总链接,本人发表这个系列的文章链接均收录于此
视觉SLAM理论到实践系列文章链接
下面是专栏地址:
视觉SLAM理论到实践专栏
文章目录
前言
高翔博士的《视觉SLAM14讲》学习笔记的系列记录
视觉SLAM理论到实践系列(五)——非线性优化(3)
实践:曲线拟合问题
vccode配置补充
在使用 vscode 时,经常会出现库文件不能识别,导致在 #include<> 处报红字的情况,这时可以按 ctrl + shift + p 来进行配置,可以手动配置,也可以选择cmake 一键配置
补充说明
由于作者写书比较早,可能由于一些历史原因,作者在代码中自己加了一个文件夹cmake,里面有两个文件,CeresConfig.cmake.in 和 FindG2O.cmake
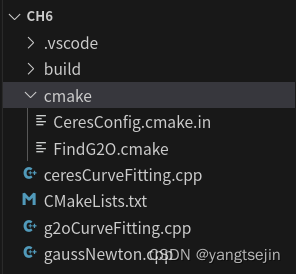
但是现在完全可以不加这两个文件,我们可以修改一下 CMakeLists.txt
注释掉下面这一行
list(APPEND CMAKE_MODULE_PATH ${PROJECT_SOURCE_DIR}/cmake)
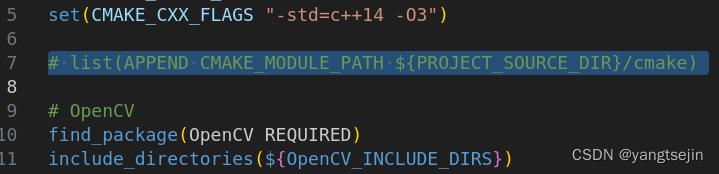
然后修改下面这一行,即将 G2O 改为 g2o
find_package(g2o REQUIRED)

再修改链接库这一行为
target_link_libraries(g2oCurveFitting ${OpenCV_LIBS} g2o::core g2o::stuff)

编译通过

手写高斯牛顿法
题目可见书上,也可见习题中的 高斯牛顿法的曲线拟合实验
使用 Ceres 进行曲线拟合
安装 Ceres
安装参考:
Ubuntu 20.04可以按照官网的方法来安装最新版本,Ubuntu 18.04则要安装老版本的Ceres 1.14.0,见上面的教程
官网:http://ceres-solver.org/
下载源码
You can start with the latest stable release . Or if you want the latest version, you can clone the git repository
git clone https://ceres-solver.googlesource.com/ceres-solver
安装依赖
# CMake
sudo apt-get install cmake
# google-glog + gflags
sudo apt-get install libgoogle-glog-dev libgflags-dev
# Use ATLAS for BLAS & LAPACK
sudo apt-get install libatlas-base-dev
# Eigen3 ,若之前安装过就不用再装了
sudo apt-get install libeigen3-dev
# SuiteSparse (optional)
sudo apt-get install libsuitesparse-dev
编译源码
tar zxf ceres-solver-2.1.0.tar.gz
mkdir ceres-bin
cd ceres-bin
cmake ../ceres-solver-2.1.0
make -j3
make test
# Optionally install Ceres, it can also be exported using CMake which
# allows Ceres to be used without requiring installation, see the documentation
# for the EXPORT_BUILD_DIR option for more information.
sudo make install
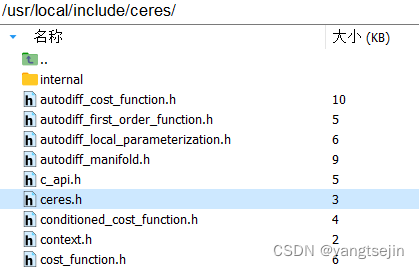
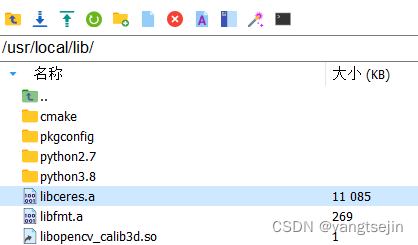
安装完成后,可以在 /usr/local/include/ceres 下找到Ceres的头文件,并在 /usr/local/lib/ 下找到名为 libceres.a 的库文件。如果能找到就代表安装成功了。
使用 g2o 进行曲线拟合
g2o 安装
安装参考:
ubuntu18.04 安装ceres,g2o,以及cmake升级
g2o官网:https://openslam-org.github.io/g2o.html
github主页:https://github.com/RainerKuemmerle/g2o
源码下载
这里不用下最新版本的,因为可能会有一些BUG,安装老版本的即可,如
安装依赖
(1)必需依赖
- C++17 compiler (CI pipeline runs with gcc, clang and MSVC)
- cmake http://www.cmake.org
- Eigen3 http://eigen.tuxfamily.org
On Ubuntu / Debian these dependencies are resolved by installing the following packages.
- cmake
- libeigen3-dev
在装g2o的时候,对 cmake 的版本有要求,可能需要升级
查看当前cmake版本:
cmake -version
卸载当前cmake:(如果安装了ROS跳过此步)
sudo apt remove cmake
下载cmake:
可直接从cmake官网下载新版本,也可执行如下语句:
wget http://www.cmake.org/files/v3.16/cmake-3.16.6.tar.gz
我这里下载的是 cmake-3.16.6版本。
(2)可选依赖
- spdlog https://github.com/gabime/spdlog
- suitesparse http://faculty.cse.tamu.edu/davis/suitesparse.html
- Qt5 http://qt-project.org
- libQGLViewer http://www.libqglviewer.com
安装命令:
sudo apt-get install libspdlog-dev libsuitesparse-dev qtdeclarative5-dev qt5-qmake libqglviewer-dev-qt5
编译并安装
cd g2o
mkdir build
cd build
sudo ldconfig # 实际安装时不写这一行也行
# cmake ..
# 注意这里官网说要用 c++17 来编译
cmake .. -DCMAKE_CXX_STANDARD=17
make -jx
sudo make install
注意,一定要在编译前进入build,进行sudo ldconfig。
ldconfig是一个动态链接库管理命令
安装完成某个工程后生成许多动态库,为了让这些动态链接库为系统所共享,还需运行动态链接库的管理命令–ldconfig。(直接sudo ldconfig即可)。
这里编译时,官网推荐选择 c++ 17 标准来编译,方法为
(1)直接使用命令
cmake .. -DCMAKE_CXX_STANDARD=17
(2)在 CMakeLists.txt 中加一行
set(CMAKE_CXX_FLAGS "-std=c++17 -O3")
g2o 库编译完成后安装

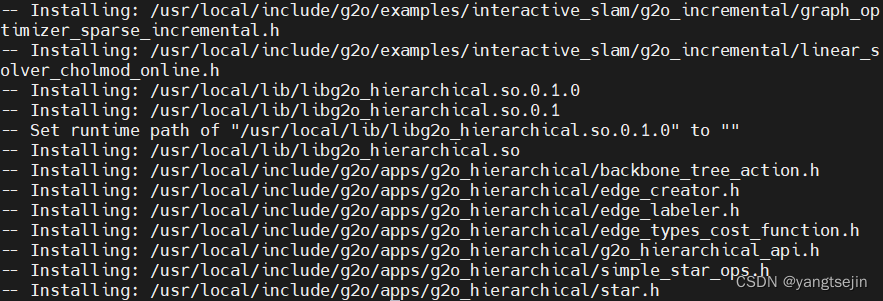
错误
错误1
再编译时出现错误
/usr/bin/ld: /home/jin/anaconda3/lib/libQt5Core.so.5.15.2: undefined reference to `std::__exception_ptr::exception_ptr::_M_release()@CXXABI_1.3.13'
/usr/bin/ld: /home/jin/anaconda3/lib/libQt5Widgets.so.5.15.2: undefined reference to `std::__throw_bad_array_new_length()@GLIBCXX_3.4.29'
/usr/bin/ld: /home/jin/anaconda3/lib/libQt5Core.so.5.15.2: undefined reference to `std::__exception_ptr::exception_ptr::_M_addref()@CXXABI_1.3.13'
collect2: error: ld returned 1 exit status
make[2]: *** [g2o/apps/g2o_viewer/CMakeFiles/g2o_viewer.dir/build.make:101:bin/g2o_viewer] 错误 1
make[1]: *** [CMakeFiles/Makefile2:1508:g2o/apps/g2o_viewer/CMakeFiles/g2o_viewer.dir/all] 错误 2
make: *** [Makefile:152:all] 错误 2
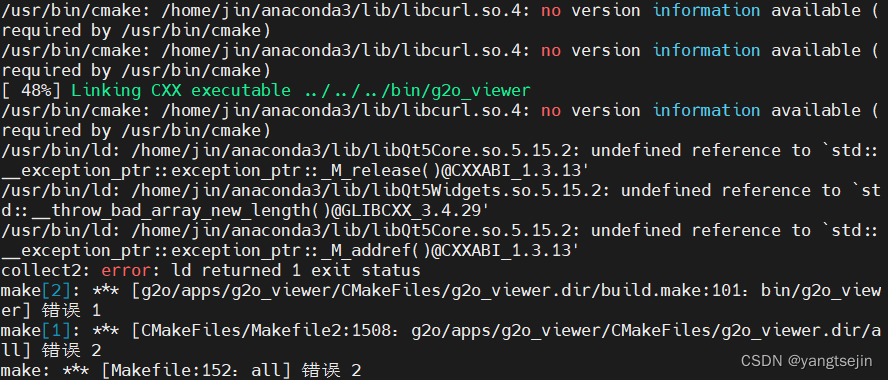
通过undefined reference to可以看出来是由于so库的引用问题导致的,我们通过修改一下配置文件,将/root/anaconda3/lib添加到用户配置文件的目录下即可
参考:
安装darknet报libQt5Core.so.5: undefined reference
解决办法
在安装ROS和安装Anaconda时都会有安装qt,同时创建了两个有关于qt的cmake文件,在编译的时候选择了有一步
find_package(Qt5 REQUIRED ...)
这一步原本应该去寻找 /usr/lib/x86_64-linux-gnu/cmake/Qt5/QtConfig.cmake 这个文件
但由于安装了 anaconda 所以这一步变为了寻找 /home/${username}/Anaconda3/lib/cmake/Qt5/QtConfig.cmake 这个文件,导致后续编译时链接的库文件出错。所以报出以上错误。
限定我们要寻找的 Qt5config.cmake 文件的路径,也就是在 CMakeLists.txt 里添加
SET(CMAKE_PREFIX_PATH "/usr/lib/x86_64-linux-gnu/cmake")
重新编译即可解决问题。(如果问题没有得到解决,建议删除build文件夹下的所有内容,再次编译,即可通过)
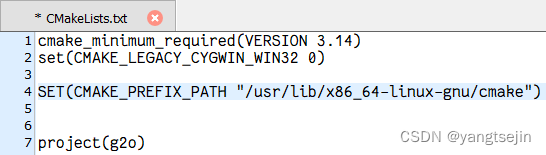
此时再编译即可编译通过
错误2
参考:
error::make_unique is not a member of ‘std’
视觉Slam14讲第六章g2o安装报错,Ubuntu22.04
error: no matching function for call to ‘g2o #206
g2o 库编译完后,在编译主函数时会报如下错误


/home/jin/jin_ws/slambook2-master/ch6/g2oCurveFitting.cpp:91:37: error: expected primary-expression before ‘>’ token
91 | g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));
| ^
/home/jin/jin_ws/slambook2-master/ch6/g2oCurveFitting.cpp:91:44: error: ‘make_unique’ is not a member of ‘g2o’; did you mean ‘std::make_unique’?
91 | g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));
| ^~~~~~~~~~~
这里可以换成老版本的 g2o 来编译安装,如 20201223 这个版本
用老本版编译安装后,就可以正常编译main函数了

图优化理论简介
我们已经介绍了非线性最小二乘的求解方式。它们是由很多个误差项之和组成的。然而,目标函数仅描述了优化变量和许多个误差项,但我们尚不清楚它们之间的关联。例如,某个优化变量 x x x ,存在于多少个误差项中呢?我们能保证对它的优化是有意义的吗?进一步,我们希望能够直观地看到该优化问题长什么样。于是,就牵涉到了图优化。
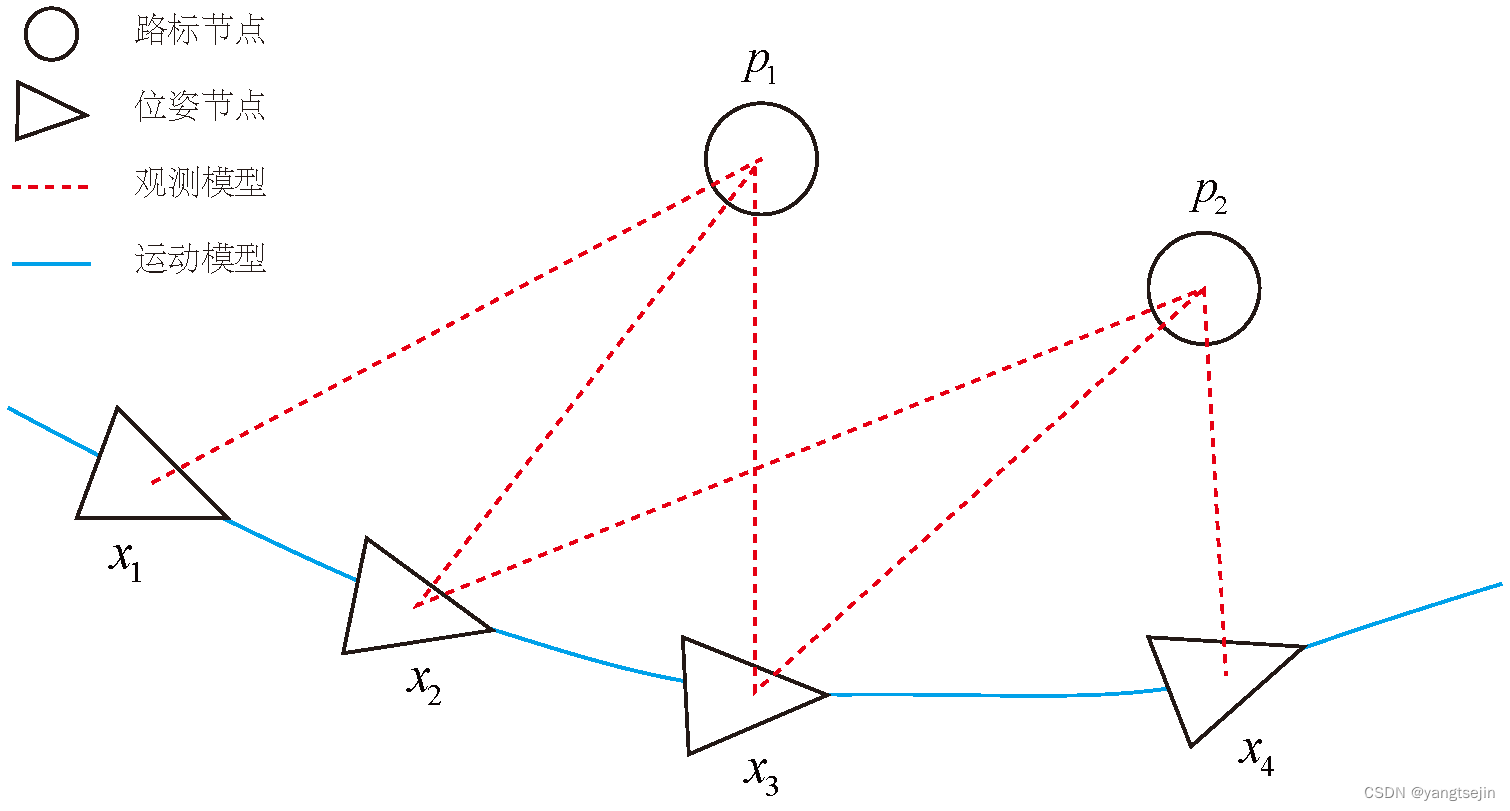
图优化,是把优化问题表现成图的一种方式。这里的图是图论意义上的图。一个图由若干个顶点(Vertex),以及连接着这些顶点的边(Edge)组成。进而,用顶点表示优化变量,用边表示误差项。于是,对任意一个上述形式的非线性最小二乘问题,我们可以构建与之对应的一个图。我们可以简单地称它为图,也可以用概率图里的定义,称之为贝叶斯图或因子图。
下图是一个简单的图优化例子。我们用三角形表示相机位姿节点,用圆形表示路标点,它们构成了图优化的顶点:同时,实线表示相机的运动模型,虚线表示观测模型,它们构成了图优化的边。此时,虽然整个问题的数学形式仍是式(6.13)那样,但现在我们可以直观地看到问题的结构了。
如果希望,也可以做去掉孤立顶点或优先优化边数较多(或按图论的术语,度数较大)的顶点这样的改进。但是最基本的图优化是用图模型来表达一个非线性最小二乘的优化问题。而我们可以利用图模型的某些性质做更好的优化。
使用 g2o 拟合曲线
为了使用 g2o,首先要将曲线拟合问题抽象成图优化。这个过程中,只要记住节点为优化变量,边为误差项可。曲线拟合对应的图优化模型可以画成下图所示的形式。
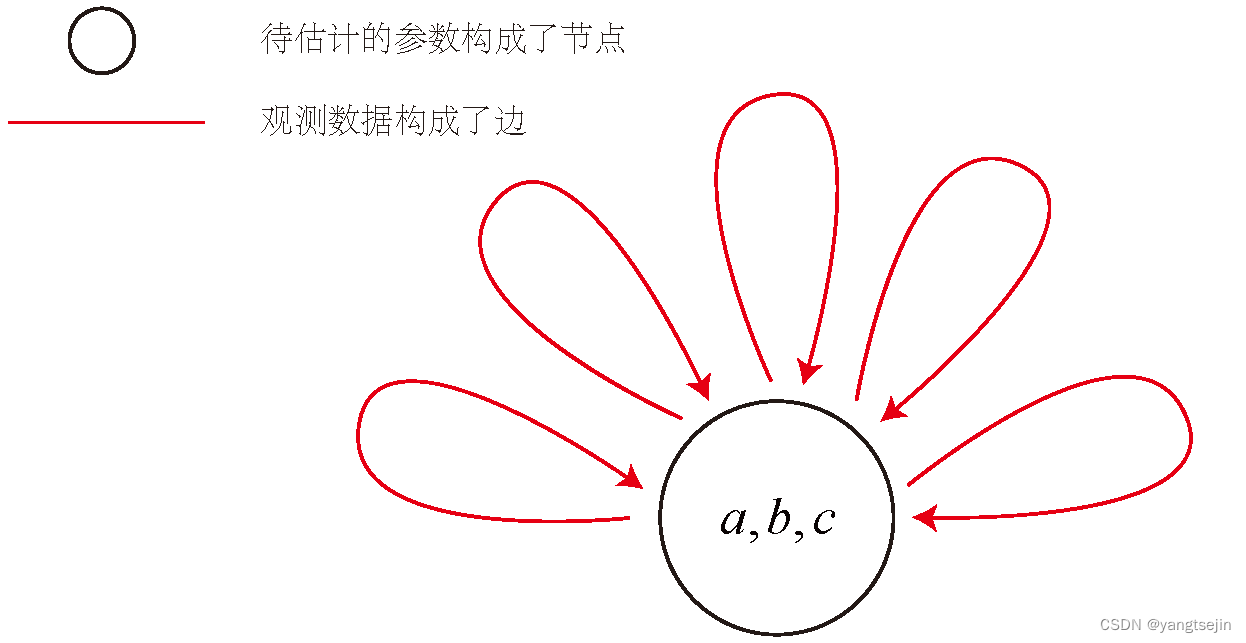
在曲线拟合问题中,整个问题只有一个顶点:曲线模型的参数是α,b,c;而各个带噪声的数据点,构成了一个个误差项,也就是图优化的边。但这里的边与我们平时想的边不太一样,它们是一元边(Unary Edge),即只连接一个顶点——因为整个图只有一个顶点。所以在上图中,我们只能把它画成自己连到自己的样子。事实上,图优化中一条边可以连接一个、两个或多个顶点,这主要反映每个误差与多少个优化变量有关。在稍有些玄妙的说法中,我们把它叫作超边(Hyper Edge),整个图叫作超图(Hyper Graph)。
弄清了这个图模型之后,接下来就是在 g2o 中建立该模型进行优化。作为 g2o 的用户,我们要做的事主要包含以下步骤:
- 定义顶点和边的类型。
- 构建图。
- 选择优化算法。
- 调用 g2o 进行优化,返回结果。
这部分和Ceres是非常相似的,当然程序在书写上会有一些不同。
本章习题
矩阵微分 (2 分,约 1.5 小时)
在优化中经常会遇到矩阵微分的问题。例如,当自变量为向量
x
\text{x}
x,求标量函数
u
(
x
)
u(\text{x})
u(x) 对
x
\text{x}
x 的导数时,即为矩阵微分。通常线性代数教材不会深入探讨此事,这往往是矩阵论的内容。我在 ppt/ 目录下为你准备了一份清华研究生课的矩阵论课件(仅矩阵微分部分)。阅读此 ppt ,回答下列问题:
设变量为 x ∈ R N \text{x}\in \mathbb{R}^N x∈RN,那么:
-
矩阵 A ∈ R N × N \text{A}\in \mathbb{R}^{N\times N} A∈RN×N,那么 d ( Ax ) d x \frac{d(\text{Ax})}{d\text{x}} dxd(Ax) 是什么1?
-
矩阵 A ∈ R N × N \text{A}\in \mathbb{R}^{N\times N} A∈RN×N,那么 d ( x T Ax ) d x \frac{d(\text{x}^{\text{T}}\text{Ax})}{d\text{x}} dxd(xTAx) 是什么?
-
证明:
x A T x = t r ( A x x T ) . \mathbf{xA}^{\mathrm{T}}\mathbf{x}=\mathrm{tr}(\mathbf{Axx}^{\mathrm{T}}). xATx=tr(AxxT).
高斯牛顿法的曲线拟合实验 (3 分,约 2 小时)
此题即为书上的 6.3.1 手写高斯牛顿法
我们在课上演示了用 Ceres 和 g2o 进行曲线拟合的验,可以看到优化框架给我们带来了诸多便利。本题中你需要自己实现一遍高斯牛顿的迭代过程,求解曲线的参数。我们将原题复述如下。设有曲线满足以下方程:
y
=
exp
(
a
x
2
+
b
x
+
c
)
+
w
y=\exp(ax^{2}+bx+c)+w
y=exp(ax2+bx+c)+w
其中
a
,
b
,
c
a,b,c
a,b,c 为曲线参数,
w
w
w 为噪声,满足
w
∼
N
(
0
,
σ
2
)
w\sim N(0,\sigma^2)
w∼N(0,σ2)。
现有 N N N 个数据点 ( x , y ) (x,y) (x,y),希望通过此 N N N 个点来拟合 a , b , c a,b,c a,b,c。实验中取 N = 100 N=100 N=100。
那么,定义误差为
e
i
=
y
i
−
exp
(
a
x
i
2
+
b
x
i
+
c
)
e_i=y_i-\exp(ax^2_i+bx_i+c)
ei=yi−exp(axi2+bxi+c),于是
(
a
,
b
,
c
)
(a,b,c)
(a,b,c) 的最优解可通过解以下最小二乘获得:
min
a
,
b
,
c
1
2
∑
i
=
1
N
∥
y
i
−
exp
(
a
x
i
2
+
b
x
i
+
c
)
∥
2
\operatorname*{min}_{a,b,c}{\frac{1}{2}}\sum_{i=1}^{N}\left\|y_{i}-\exp\left(ax_{i}^{2}+bx_{i}+c\right)\right\|^{2}
a,b,cmin21i=1∑N
yi−exp(axi2+bxi+c)
2
现在请你书写 Gauss–Newton 的程序以解决此问题。程序框架 code/gaussnewton.cpp,请填写程序内容以完成作业。作为验证,按照此程序的设定,估计得到的
a
,
b
,
c
a,b,c
a,b,c 应为:
a
=
0.890912
,
b
=
2.1719
,
c
=
0.943629.
a=0.890912,b=2.1719,c=0.943629.
a=0.890912,b=2.1719,c=0.943629.
这和书中的结果是吻合的。
解答
雅可比矩阵形式如下:
J
(
x
k
)
=
[
∂
F
(
x
)
∂
x
1
,
.
.
.
,
∂
F
(
x
)
∂
x
n
]
T
\mathrm{J\left(x_k\right)=[\frac{\partial F\left(x\right)}{\partial x_1},...,\frac{\partial F\left(x\right)}{\partial x_n}]^T}
J(xk)=[∂x1∂F(x),...,∂xn∂F(x)]T
可以求得每个误差项对于状态变量的导数为
∂
e
i
∂
a
=
−
x
i
2
exp
(
a
x
i
2
+
b
x
i
+
c
)
∂
e
i
∂
b
=
−
x
i
exp
(
a
x
i
2
+
b
x
i
+
c
)
∂
e
i
∂
c
=
−
exp
(
a
x
i
2
+
b
x
i
+
c
)
\begin{aligned} \frac{\partial e_i}{\partial a} &=-x_i^2\exp\left(ax_i^2+bx_i+c\right) \\\\ \frac{\partial e_i}{\partial b} &=-x_i\exp\left(ax_i^2+bx_i+c\right) \\\\ \frac{\partial e_{i}}{\partial c} &=-\exp\left(ax_i^2+bx_i+c\right) \end{aligned}
∂a∂ei∂b∂ei∂c∂ei=−xi2exp(axi2+bxi+c)=−xiexp(axi2+bxi+c)=−exp(axi2+bxi+c)
此题中,雅可比矩阵即一阶导为:
J
i
=
[
∂
e
i
∂
a
∂
e
i
∂
b
∂
e
i
∂
c
]
=
[
−
x
i
2
exp
(
a
x
i
2
+
b
x
i
+
c
)
−
x
i
exp
(
a
x
i
2
+
b
x
i
+
c
)
−
exp
(
a
x
i
2
+
b
x
i
+
c
)
]
J_i= \left[ \begin{matrix} \frac{\partial e_i}{\partial a}\\ \frac{\partial e_i}{\partial b}\\ \frac{\partial e_i}{\partial c} \end{matrix}\right]= \left[ \begin{matrix} -x_i^2\exp\left(ax_i^2+bx_i+c\right)\\ -x_i\exp\left(ax_i^2+bx_i+c\right)\\ -\exp\left(ax_i^2+bx_i+c\right) \end{matrix} \right]
Ji=
∂a∂ei∂b∂ei∂c∂ei
=
−xi2exp(axi2+bxi+c)−xiexp(axi2+bxi+c)−exp(axi2+bxi+c)
高斯牛顿法的增量方程为:
Δ
x
∗
=
−
(
J
(
x
)
J
T
(
x
)
)
−
1
J
(
x
)
f
(
x
)
\Delta\boldsymbol{x}^*=-\left(J(\boldsymbol{x})J^{T}\left(\boldsymbol{x}\right)\right)^{-1}J(\boldsymbol{x})f\left(\boldsymbol{x}\right)
Δx∗=−(J(x)JT(x))−1J(x)f(x)
实际上也可以看成求解非齐次方程
H
x
=
b
Hx=b
Hx=b:
J
(
x
)
J
T
(
x
)
⏟
H
(
x
)
Δ
x
=
−
J
(
x
)
f
(
x
)
⏟
g
(
x
)
\begin{gathered} \underbrace{J(x)J^{\mathrm{T}}\left(\boldsymbol{x}\right)}_{H(x) }\Delta x=\underbrace{-J(\boldsymbol{x})f\left(\boldsymbol{x}\right)}_{g(x)} \\ \end{gathered}
H(x)
J(x)JT(x)Δx=g(x)
−J(x)f(x)
此题中
f
(
x
)
f(x)
f(x) 即为
e
i
=
y
i
−
exp
(
a
x
i
2
+
b
x
i
+
c
)
e_i=y_i-\exp(ax^2_i+bx_i+c)
ei=yi−exp(axi2+bxi+c)
那么在这里为:
J
J
T
[
Δ
a
Δ
b
Δ
c
]
=
−
J
⋅
e
i
[
Δ
a
Δ
b
Δ
c
]
=
−
(
J
J
T
)
−
1
J
e
i
\begin{aligned} JJ^T \left[ \begin{matrix} \Delta a\\ \Delta b\\ \Delta c \end{matrix} \right] &= -J\cdot e_i \\\\ \left[ \begin{matrix} \Delta a\\ \Delta b\\ \Delta c \end{matrix} \right] &=-(JJ^T)^{-1} J e_i \end{aligned}
JJT
ΔaΔbΔc
ΔaΔbΔc
=−J⋅ei=−(JJT)−1Jei
于是
J
i
=
[
∂
e
i
∂
a
,
∂
e
i
∂
b
,
∂
e
i
∂
c
]
T
\boldsymbol{J}_i=\left[\frac{\partial e_i}{\partial a},\frac{\partial e_i}{\partial b},\frac{\partial e_i}{\partial c}\right]^\mathrm{T}
Ji=[∂a∂ei,∂b∂ei,∂c∂ei]T,高斯牛顿法的增量方程为
(
∑
i
=
1
100
J
i
(
σ
2
)
−
1
J
i
T
)
Δ
x
k
=
∑
i
=
1
100
−
J
i
(
σ
2
)
−
1
e
i
,
\left(\sum_{i=1}^{100}\boldsymbol{J}_{i}(\sigma^{2})^{-1}\boldsymbol{J}_{i}^{\mathrm{T}}\right)\Delta\boldsymbol{x}_{k}=\sum_{i=1}^{100}-\boldsymbol{J}_{i}(\sigma^{2})^{-1}e_{i},
(i=1∑100Ji(σ2)−1JiT)Δxk=i=1∑100−Ji(σ2)−1ei,
这个公式是高翔书上给的,不加 ( σ 2 ) − 1 (\sigma^2)^{-1} (σ2)−1 这一项的话可以当作自己写代码的练习
当然,我们也可以选择把所有的 J i J_i Ji 排成一列,将这个方程写成矩阵形式,不过它的含义与求和形式是一致的。
注意:
这里的高斯牛顿方程多了一项 ( σ 2 ) − 1 (\sigma^2)^{-1} (σ2)−1 ,即方差的倒数,有点信息矩阵的意思
对于每次一迭代,计算代价(即损失)的代码如下
for (int i = 0; i < N; i++) {
double xi = x_data[i], yi = y_data[i]; // 第i个数据点
double error = yi - exp(ae * xi * xi + be * xi + ce);
Vector3d J; // 雅可比矩阵
J[0] = -xi * xi * exp(ae * xi * xi + be * xi + ce); // de/da
J[1] = -xi * exp(ae * xi * xi + be * xi + ce); // de/db
J[2] = -exp(ae * xi * xi + be * xi + ce); // de/dc
// 这里累加的意思将所有点的 J_i(J_i)^T 加起来作为 H , 将 -J_if(x) 即 -J_ie_i 加起来作为 b
H += inv_sigma * inv_sigma * J * J.transpose();
b += -inv_sigma * inv_sigma * error * J;
//将所有点的误差数据的平方相加作为代价
cost += error * error;
}
求解 Hx=b
// 求解线性方程 Hx=b
Vector3d dx = H.ldlt().solve(b);
处理一下得到的结果
if (isnan(dx[0])) {
std::cout << "result is nan!" << endl;
break;
}
if (iter > 0 && cost > lastCost) {
// 误差增长了,说明近似的不够好,直接break
std::cout << "cost: " << cost << ", last cost: " << lastCost << endl;
break;
}
// 更新abc估计值
ae += dx[0];
be += dx[1];
ce += dx[2];
lastCost = cost;
std::cout << "total cost: " << cost << endl;
}
std::cout << "estimated abc = " << ae << ", " << be << ", " << ce << endl;
return 0;
运行结果如下:

源代码如下
#include <iostream>
#include <chrono>
#include <opencv2/opencv.hpp>
#include <Eigen/Core>
#include <Eigen/Dense>
using namespace std;
using namespace Eigen;
int main(int argc, char **argv) {
double ar = 1.0, br = 2.0, cr = 1.0; // 真实参数值
double ae = 2.0, be = -1.0, ce = 5.0; // 估计参数值
int N = 100; // 数据点
double w_sigma = 1.0; // 噪声Sigma值
double inv_sigma = 1.0 / w_sigma;
cv::RNG rng; // OpenCV随机数产生器
vector<double> x_data, y_data; // 数据
for (int i = 0; i < N; i++) {
double x = i / 100.0;
x_data.push_back(x);
y_data.push_back(exp(ar * x * x + br * x + cr) + rng.gaussian(w_sigma * w_sigma));
}
// 开始Gauss-Newton迭代
int iterations = 100; // 迭代次数
double cost = 0, lastCost = 0; // 本次迭代的cost和上一次迭代的cost
chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
for (int iter = 0; iter < iterations; iter++) {
Matrix3d H = Matrix3d::Zero(); // Hessian = J^T W^{-1} J in Gauss-Newton
Vector3d b = Vector3d::Zero(); // bias
cost = 0;
for (int i = 0; i < N; i++) {
double xi = x_data[i], yi = y_data[i]; // 第i个数据点
double error = yi - exp(ae * xi * xi + be * xi + ce);
Vector3d J; // 雅可比矩阵
J[0] = -xi * xi * exp(ae * xi * xi + be * xi + ce); // de/da
J[1] = -xi * exp(ae * xi * xi + be * xi + ce); // de/db
J[2] = -exp(ae * xi * xi + be * xi + ce); // de/dc
H += inv_sigma * inv_sigma * J * J.transpose();
b += -inv_sigma * inv_sigma * error * J;
cost += error * error;
}
// 求解线性方程 Hx=b
Vector3d dx = H.ldlt().solve(b);
if (isnan(dx[0])) {
cout << "result is nan!" << endl;
break;
}
if (iter > 0 && cost >= lastCost) {
// 误差增长了,说明近似的不够好,直接break
cout << "cost: " << cost << ">= last cost: " << lastCost << ", break." << endl;
break;
}
// 更新abc估计值
ae += dx[0];
be += dx[1];
ce += dx[2];
lastCost = cost;
cout << "total cost: " << cost << ", \t\tupdate: " << dx.transpose() <<
"\t\testimated params: " << ae << "," << be << "," << ce << endl;
}
chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
cout << "solve time cost = " << time_used.count() << " seconds. " << endl;
cout << "estimated abc = " << ae << ", " << be << ", " << ce << endl;
return 0;
}
对应的 CMakeLists.txt 为
cmake_minimum_required(VERSION 2.8)
set(EXECUTABLE_OUTPUT_PATH ${CMAKE_CURRENT_SOURCE_DIR}/bin)
find_package(OpenCV REQUIRED)
include_directories(${OpenCV_INCLUDE_DIRS})
include_directories("/usr/include/eigen3")
add_executable(gaussnewton gaussnewton.cpp)
target_link_libraries(gaussnewton ${OpenCV_LIBS})
严格的写法必须对⾏向量求导,所以应该写成 d ( Ax ) d x T \frac{d(\text{Ax})}{d\text{x}^{\text{T}}} dxTd(Ax)。但有些时候我们为了公式简洁,也会省略这个 T \text{T} T ↩︎






















 892
892

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








