浅谈白化（Whitening） 、PCA白化、ZCA白化

白化

本节讨论白化（Whitening），以及白化与 PCA（Principal Component Analysis） 和 ZCA（Zero-phase Component Analysis） 的关系。

备注：这是一篇对白化新的理解，可以和之前写过的一篇白化博客对照看机器学习中的数学（十）：白化（whitening）

对数据做白化处理后相比于原始数据有两个特点：

1. 数据的不同维度去相关；

2. 数据每个维度的方差为1；

条件1要求白化后数据的协方差矩阵是个对角阵；条件2要求白化后数据的协方差矩阵是个单位矩阵。

白化作用如图：

为什么使用白化？

假设训练数据是图像，由于图像中相邻像素之间具有很强的相关性，所以用于训练时输入是冗余的。白化的目的就是降低输入的冗余性。

比如在独立成分分析（ICA）中，对数据做白化预处理可以去除各观测信号之间的相关性，从而简化了后续独立分量的提取过程，而且，通常情况下，数据进行白化处理与不对数据进行白化处理相比，算法的收敛性较好。

PCA白化 与 ZCA白化

PCA 白化

给定训练数据集（假设每个特征都具有零均值）：

n 是数据维度；m 是样本个数。

数据的协方差矩阵为：

对协方差矩阵做奇异值分解：

U 是 Σ 的特征向量矩阵，S 是其特征值矩阵；因为 Σ 是对称方阵，所以 V=U'，Σ=USV。

PCA 白化的定义如下：

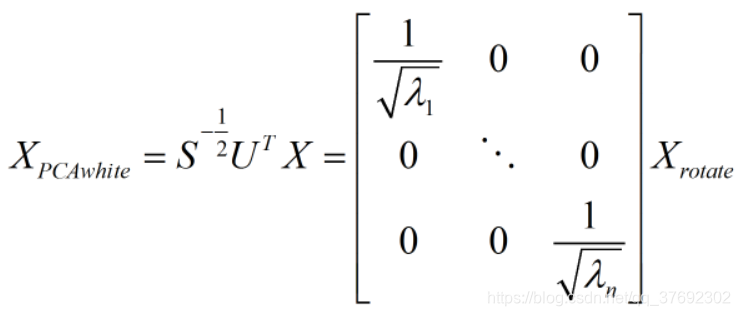
其中，Xrotate 就是原数据在主成分轴上的投影，而 S^(-1/2) 相当于对每一个主轴上的数据做一个缩放，缩放因子就是除以对应特征值的平方根。

所以：

上式第 2 步是把 XPCAwhite 表达式带入得到的；第 3 步利用了矩阵 S 是对角阵的特性；第 4 步是将 Σ 作奇异值分解得到的；第 5 步利用了 U 是酉矩阵的性质（U'U=UU'=I）。

可见数据在经过 PCA 白化以后，其协方差矩阵是一个单位矩阵，即各维度变得不相关，且每个维度方差都是 1。

ZCA 白化

教程里给 ZCA 白化的定义是：

相当于将经过 PCA 白化后的数据重新变换回原来的空间。

所以：

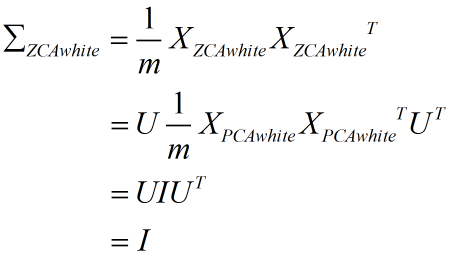
可见 ZCA 白化也是一个合法的白化。

PCA 白化 与 ZCA 白化

如何理解两者之间的关系？

首先，PCA 白化将原数据变换（投影）到主成分轴上，这一步消除了特征之间的相关性；

其次，PCA 白化对每一个主成分轴上的数据进行缩放，使其方差为 1；

因为以上的线性变换是在主成分空间中完成的，为了使白化后的数据尽可能接近原数据，可以把处理过的数据再变换回原空间，也就是 ZCA 白化。

ZCA 白化的全称是 Zero-phase Component Analysis Whitening。我对【零相位】的理解就是，相对于原来的空间（坐标系），白化后的数据并没有发生旋转（坐标变换）。

正则化

在实践中，PCA 与 ZCA 白化都需要被正则化（Regularization）。即在缩放这个步骤之前，给每一个特征值先加上一个正则化项：

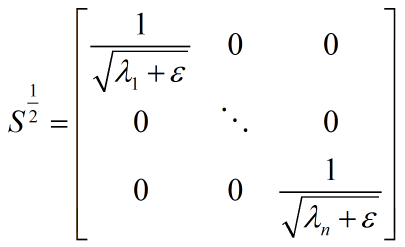
教程给出的原因有两个：

1. 有时一些特征值在数值上接近0，在缩放步骤时将导致除以一个接近0的值；这可能使数据上溢或造成数值不稳定；

2. 对图像来说，正则化项对输入图像也有一些平滑去噪（或低通滤波）的作用，可改善学习到的特征。

以 PCA 白化为例，经过正则化的数据协方差矩阵为：

相当于减小了每个像素的不确定性（方差）。

关于低通滤波，可以这样理解：

最简单的低通滤波就是把一个像素的色值替换为其周围像素色值的算术平均。可以想象，经过处理之后的图像色彩变化更平缓，图像变得更模糊。

为什么要这样做？首先，数字图像总是伴随着噪点。其次，噪点总是伴随着色值的剧烈变化，因为每个噪点都是独立产生的。但是原图像的像素之间并不是独立的，表现为多像素构成的“色块”。

低通滤波器对“剧烈的"、"高频的”变化更敏感，所以它对噪音的影响大于对原图像的影响。经过低通滤波处理的图像可以展示出原本被噪音掩盖的细节。

对图像进行PCA白化和ZCA白化后实验结果对比：

图1：原始数据

 

图2：零均值化以后的数据

图3：PCA 白化所使用的基

图4：ZCA 白化所使用的基：

本例使用的图片尺寸均为 12×12，数据具有 144 个维度，可以认为ZCA 白化的每一个基都处于其中一个维度（一个像素），即 ZCA 白化针对原数据每一个维度分别提取特征，而 PCA 白化是针对进行主成分变换后的数据的每一个维度提取特征，前者是高度局部化的，后者着眼于全局。

图5：PCA 白化后的数据

图6：ZCA 白化后的数据：

显然 ZCA 白化相比 PCA 白化更接近原数据。