二叉排序树和平衡二叉树

二叉排序树

定义

二叉排序树或者是空树，或者是满足以下性质的二叉树：
1）左子树不为空，则左子树上所有关键字的值均小于根关键字的值。
2）右子树不为空，则右子树上所有关键字的值均大于根关键字的值。
3）左右子树各是一棵二叉排序树。

存储结构

二叉排序树采用二叉链表进行存储，结点类型类似于一般的二叉树。

typedef struct BTNode
{
    int key; // 关键字
    struct BTNode *lchild; // 左指针域
    struct BTNode *rchild; // 右指针域
}BTNode;

基本算法

查找关键字

由以下过程可以看出，二叉树的查找过程和折半（二分）查找的过程十分相似，实际上折半查找的判定树就是一棵二叉排序树。

1. 将待查关键字与根结点的关键字比较，相等则查找成功。
2. 小于根结点的关键字则前往左子树查找，大于根结点的关键字则前往右子树查找。
3. 重复1、2操作，直到查找成功或者来到了结点的空指针域，说明查找失败。

要注意的一点是，若要计算查找的次数，第一次与根结点的比较也是要算入的。

BTNode* BSTSearch(BTNode* bt, int key)
{
    if (bt == NULL)
        return NULL; // 来到空指针域，查找不成功返回NULL
    else
    {
        if (key == bt->key) // 查找成功返回关键字所在结点指针
            return bt;
        else if (key < bt->key) // 小于根结点关键字前往左子树
            return BSTSearch(bt->lchild, key); // 该查找函数有返回值，所以递归调用时要用return
        else // 大于根结点关键字前往左子树
            return BSTSearch(bt->rchild, key);
    }
}

关键字插入

二叉树作为一个动态集合，其特点是树的结构通常不是一次生成的，而是在查找过程中，当树中不存在关键字值等于给定值的结点时再进行插入的。
先找插入的位置，插入的位置为该关键字在二叉排序树中查找不成功的位置，前提是该二叉排序树不存在该关键字。在二叉排序树中插入新的关键字均存储在新创建的叶结点上，由于找到的插入位置总是在空指针域上，因此在空指针域上连接的一个新结点必为叶结点。

int BSTInsert(BTNode *&bt, int key) // 指针bt要改变，所以用引用型指针
{
    // 在外部函数定义结构体指针时
    // 程序只会给指针分配能存放地址的空间
    // 并不会为该结构单元开辟内存空间，那什么时候开辟呢？
    // 在C中用malloc，在C++中用new时才会真正的分配内存空间
    // 此时再将地址返回指针，指针的内存空间中就存入了新内存空间的地址
    // 所以此处如果不用引用型指针，仅仅传入形参指针
    // 在该函数中，在bt == NULL后，新建一个结点时，结点的地址仅仅保存在形参指针中
    // 所以在退出这个函数之后，该地址就丢失了，并没有插入二叉排序树中
    // 所以如果我们传入指针的引用，新建结点时，就直接将新结点的地址给到了bt，并不会丢失
    if (bt == NULL)
    {
        bt = new BTNode; // 创建新结点
        // bt = (BTNode*)malloc(sizeof(BTNode));
        bt->lchild = bt->rchild = NULL; // 来到空指针域表明找到插入位置
        bt->key = key;
        return 1; // 插入成功，返回1
    }
    else
    {
        if (key == bt->key) // 关键字已存在于树中，插入失败，返回0
            return 0;
        else if (key < bt->key)
            return BSTInsert(bt->lchild, key);
        else
            return BSTInsert(bt->rchild, key);
    }
}

二叉排序树的构造

若从空树出发，经过一系列的查找插入操作之后，可生成一棵二叉树。设查找的关键字序列为{45, 24, 53, 45, 12, 24, 90}，则生成的二叉排序树如图所示。

容易看出，中序遍历二叉排序树可得到一个关键字的有序序列，这个性质是由二叉排序树的定义决定的。也就是说，一个无序序列可以通过构造一棵二叉排序树从而变成一个有序序列，构造树的过程即为对无序序列进行排序的过程。不仅如此，从上面的插入过程还可以看到，每次插入的新结点都是二叉排序树上新的叶子结点，则在进行插入操作时，不必移动其他结点，仅需改动某个结点的指针，由空变为非空即可。这就相当于在一个有序序列上插入一个记录而不需要移动其他记录。它表明，二叉排序树既拥有类似于折半查找的特性，又采用了链表作为存储结构，因此是动态查找表的一种适宜表示。

void CreateBST(BTNode *&bt, int key[], int n)
{
    int i;
    bt = NULL; // 将树清空
    for (int i = 0;i < n; ++i) // 调用插入函数，逐个插入关键字
        BSTInsert(bt, key[i]);
}

删除关键字

对于一般的二叉树来说，删去树中一个结点是没有意义的，因为它将使以被删结点为根的子树称为森林，破坏了整棵树的结构。
删除关键字要注意，不能把以该关键字所在的结点为根的子树都删除，而是删除这一个结点，并保持二叉排序树的特性。
假设所在二叉排序树上被删除结点为p，f为其双亲结点，则删除结点p的过程分为以下3种情况：

1. p为叶结点直接删除p。
2. p只有单一子树，直接将子树连接在f上然后删除p。
3. p既有左子树又有右子树，则令p的直接后继（或直接前驱）替代p（替换关键字），然后从二叉排序树中删去这个直接后继（或直接前驱），这样就转换成了前两种情况。如图所示。

void DeleteBTS(BTNode *&bt, int key)
{
    if (bt == NULL) // 关键字不存在树中，删除失败，返回0
        return 0;
    else
    {
        if (key == bt->key) // 找到关键字，执行删除函数
            return Delete(bt);
        else if (key < bt->key)
            return DeleteBTS(bt->lchild, key);
        else
            return DeleteBTS(bt->rchild, key);
    }
}

void Delete(BTNode *&bt)
{
    if (bt->lchild != NULL && bt->rchild == NULL) // 右子树为空
    {
        BTNode* q = bt;
        bt = bt->lchild;
        delete(q);
    }
    else if (bt->lchild == NULL && bt->rchild != NULL) // 左子树为空
    {
        BTNode* q = bt;
        bt = bt->rchild;
        delete(q);
    }
    else // 左右子树均不为空
    {
        BTNode* q = bt;
        BTNode* s = bt->lchild;
        while (s->rchild != NULL) // 先转向左孩子，然后找最右结点，即为中序遍历下bt的直接前驱
        {
            q = s; // q记录的是s的双亲结点
            s = s->rchild;
        }
        bt->data = s->data; // 用直接前驱的关键值替换bt
        if (q != bt) // 若双亲不是待删除结点
            q->rchild = s->lchild; // s是最右结点，要么有左孩子要么没有左孩子
                                // 删除s后q会空出右指针域，所以将s的左孩子或NULL给到q的右指针域
        else // 若双亲就是待删除结点，相当于s为其左孩子也为其直接前驱
            q->lchild = s->lchild; // 删除s后q会空出左指针域，所以将s的左孩子或NULL给到q的左指针域
        delete(s);
    }
}

效率分析

对于高度为h的二叉排序树，其插入和删除操作的运行时间都是$O(h)$。但在最坏情况下，即构造二叉排序树的输入序列是有序的，则会形成一个倾斜的单支树，此时二又排序树的性能显著变坏，树的高度也增加为元素个数n，如图所示。

在等概率情况下，左图二叉排序树查找成功的平均查找长度为$$AS{L}_a=(1+2\times 2+3\times 4+4\times 3)/10=2.9$$而右图二叉排序树查找成功的平均查找长度为$$AS{L}_b=(1+2+3+4+5+6+7+8+9+10)/10=5.5$$由上可知，二叉排序树查找算法的平均查找长度，主要取决于树的高度，即与二又树的形态有关。若二叉排序树是一个只有右（左）孩子的单支树（类似于有序的单链表），则其平均查找长度和单链表相同，为$O(n)$。若二叉排序树的左、右子树的高度之差的绝对值不超过1，则这样的二又排序树称为平衡二叉树。它的平均查找长度达到$O(lo{g}_{2}n)$。
从从查找过程看，二叉排序树与折半查找相似。就平均时间性能而言，二叉排序树上的查找和折半查找差不多。但折半查找的判定树唯一，而二叉排序树的查找不唯一，相同的关键字其插入顺序不同可能生成不同的二叉排序树，就比如图中所示。
就维护表的有序性而言，二叉排序树无须移动结点，只需修改指针即可完成插入和删除操作，平均执行时间为$O(lo{g}_{2}n)$。折半查找的对象是有序顺序表，若有插入和删除结点的操作，所花的代价是$O(n)$。当有序表是静态查找表时，宜用顺序表作为其存储结构，而采用折半查找实现其查找操作；若有序表示动态查找表，则应选择二叉排序树作为其逻辑结构。

平衡二叉树

定义

由前文我们知道，在随机的情况下，二叉排序树的平均查找长度和$logn$是等数量级的。然而，在某些情况下，尚需在构成二叉排序树的过程中进行“平衡化”处理，成为平衡二叉树。
平衡二叉树又称为AVL树，是一种特殊的二叉排序树。其左右子树都是平衡二叉树，且左右子树高度之差的绝对值不超过1。一句话表述为：以树中所有结点为根的树的左右子树高度之差的绝对值不超过1。
为了判断一棵二叉排序树是否是平衡二叉树，引进了平衡因子的概念。平衡因子是针对树中的结点来说的，一个结点的平衡因子为其左子树高度减去右子树高度的差。因此对于平衡二叉树，树中的所有结点的平衡因子的取值只能是-1、0、1三个值。

平衡二又树的建立

建立平衡二叉树的过程类似于二叉排序树，都是将关键字逐个插入空树中的过程。有所不同的是，在建立平衡二叉树的过程中，每插入一个新的关键字都要检查新关键字的插入是否会使得原平衡二叉树失去平衡，直接表现为树中出现平衡因子绝对值大于1的结点。如果失去平衡则需要对平衡二叉树进行平衡调整。

平衡调整

假定向平衡二叉树中插入一个新结点后破坏了平衡二又树的平衡性，则首先要找出插入新结点后失去平衡的最小子树，然后再调整这棵子树使之成为平衡子树。值得注意的是，当失去平衡的最小子树被调整为平衡子树后，无须调整原有的，其他所有的不平衡子树，整个二又排序树就会成为一棵平衡二叉树。所谓失去平衡的最小子树是以距离插入结点最近，且以平衡因子绝对值大于1的结点作为根的子树，又称为最小不平衡子树。
当然，平衡调整必须保持二叉排序树左小右大的性质，平衡调整有4种情况，分别为LL型、RR型、LR型和RL型。

调整类型

如图所示，某时刻在b的左子树Y上插入一个结点，导致a的左子树高度为h+2，右子树高度为h，发生不平衡。此时应该将a下移一个结点高度，b上移一个结点高度，也就是将b从a的左子树取下，然后将b的右子树挂在a的左子树上，最后将a挂在b的右子树上以达到平衡。这就是LL调整，也叫右单旋转调整。如果b在a的右子树上,且插入的新结点在b的右子树上，即与最左边对称的情況，则此时只需将上述步骤中的左换成右，右换成左，做对称处理即可，这种调整叫RR调整，也叫左单旋转调整。

所示，某时刻在b的右子树Y上插入一个结点导致不平衡。此时需要将子树Y拆分成两个子树和V，根结点为c。并将b的右子树、a的左子树和c的左右子树都取下。然后将c作为a和b两棵子树的根，b为左子树，a为右子树，c原来的左子树U作为b的右子树，c原来的右子树V作为a的左子树以达到平衡。这就是LR调整，也叫先左后右双旋转调整。如果b在a的右子树上,且插入的结点在b的左子树上，即与最左边对称的情况，则此时只需将上述过程做左右对称处理即可。这种调整叫RL调整，也叫先右后左双旋转调整。

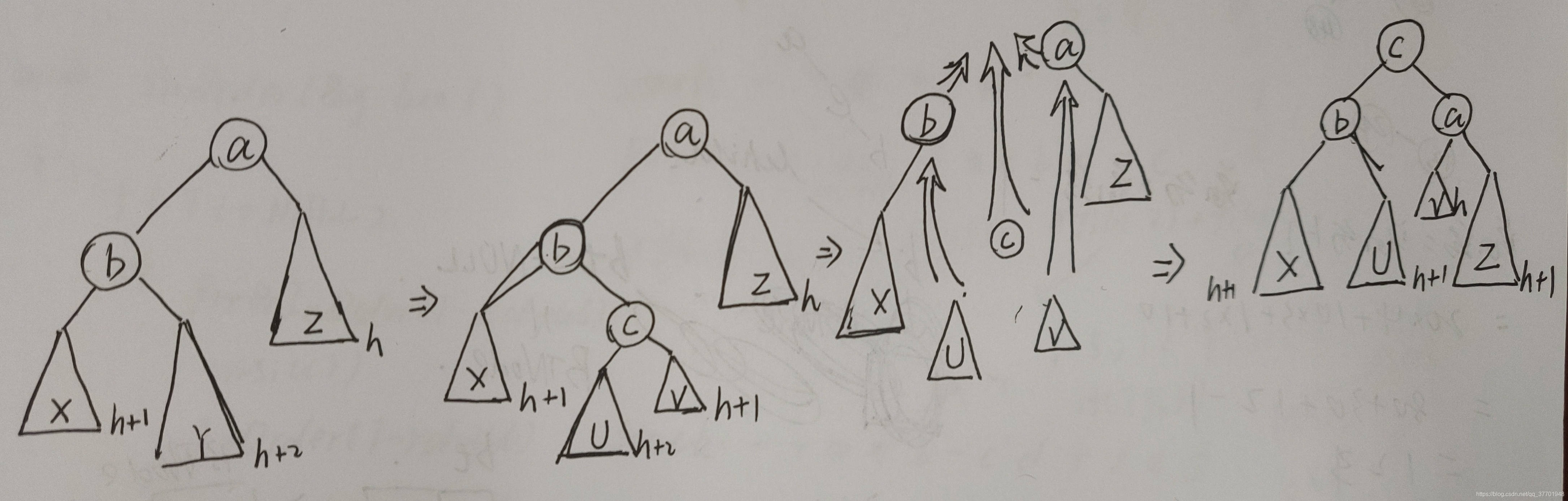
上图中显示的导致发生不平衡的结点落在子树U上只是双旋转中的一种情况，还可能落在V上，处理方法基本不变。

要注意的是，这四种调整方式的命名：LL、RR、LR、RL，并不是对调整过程的描述，而是对不平衡状态的描述。如LL( Ileft-left)调整，就是新插入结点落在最小不平衡子树根结点的左孩子的左子树上，对这种不平衡状态进行调整称之为LL调整。又如LR调整(Left- Right)，就是新插入结点落在最小不平衡子树根结点的左孩子的右子树上，对这种不平衡状态进行调整称之为LR调整。

呼，二叉树就暂时告一段落吧~~~