M×N扫描序列图像拼接、大视场图像拼接、全景图像拼接、2D网格拼图方法、累计误差消除（显微图像/航拍图像等）
前言
笔者前一段时间在做基于点云的二维定位超分辨拼图，其中临接点云两两对准算法采用JRMPC算法（经典的ICP算法对初值较为敏感），本文主要介绍获得序列图像两两变换关系后，大视场图像拼接存在的问题与拼接方法。（嗯~点云和图像在两两对准算法上不同，但大视场拼图的逻辑都一样，所以虽然做的是点云拼接但是很多地方习惯性采用了图像字眼）
笔者总共归纳出了5种拼接方法，包括：
搜索算法、最小生成树算法、全局捆绑调整算法、全局调整回路检测结合算法
一、问题描述
序列图像的获取包括下图所示的一些扫描方式，不论我们采用何种扫描方法，最终将获得许多小视场图像，这些小视场图像的大体位置可以根据扫描方式确定，而图像拼接问题就是如何根据已知大体位置关系和相邻两幅图像的变换关系(由两两图像对准算法求取)，重建出完整的大视场图像。
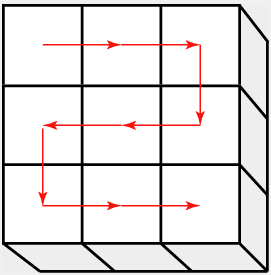
上图来自https://imagej.net/downloads的FiJi插件
二、拼接过程存在的问题
图中每个小视场的图像序列编号由扫描方式确定，代表了每个小视场图像的位置关系。由于每次扫描步进间隔不稳定，获取的小视场图像会存在一定的错位，我们需要通过配准/对准算法对相邻的图像进行两两对准以获得他们之间的变换关系（2D序列图像拼接，这里仅考虑水平x、y方向的变换关系）。
两两图像间的对准关系有了，那是不是按照下图(a)的方式，把第2张图和第一张图拼在一起，再陆续用和后面的3,4张图不断拼上去呢？如果这样做那么问题来了，我们不能保证1-2、2-3、3-4这些图像两两配准后获得的变换关系绝对正确，比如(b)图，当按照1，2，3，6，5，4的顺序依次拼接，由于两两图像配准存在误差，这一连串拼接下来，最后的1图和4图是否能对齐呢？另一方面当某两幅图像对准结果存在较大的偏差时，后续依次拼接上的图像将会产生严重的错误。
总的来说主要有以下两个问题需要考虑
1. 累计误差的影响
2. 错误配准的影响
事实上在扫描获取序列图像的过程中，扫描步进的大致范围是知道的，依据步进范围可以大体剔除严重的错误对准，但是对于对准错误较小的情况(较小的对准错误也远大于对准误差，不加以处理会产生严重的拼接错位)仍然需要认真考虑。
![[1]](https://img-blog.csdnimg.cn/20210710092456975.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzM3NzY0MTQx,size_8,color_FFFFFF,t_70)
三、4种拼接算法介绍
每张图像根据位置不同可能有2,3,4个相邻的图像，因为相邻图像两两对准过程中可能存在错误对准情况，剔除掉明显错误的连接后，每个图像节点可能的连接边有0,1,2,3,4个。(对于连接边为0的图像节点无法根据对准关系拼接，这里一般根据其图像序列，也就是扫描过程中的大致位置来给一个全局位置坐标)
1.搜索算法
搜索算法是最基本的拼接算法了。搜索算法以某一个图像节点为起始点根据邻接关系搜索其他图像节点并进行配准，配准结果如果没有因为错误过大而被剔除则认为配准成功，并搜索其他图像节点。这里就不详细介绍搜索算法原理了(算法过程可以参考文末附码)。
搜索算法不用事先把所有相邻图像都进行配准，而是一边搜索一边配准，最后总共进行的配准次数会远小于对所有相邻图像的配准。但是搜索算法并没有消除累计误差和拼接错误，其最后的大视场图像拼接效果非常依赖于对准算法的对准精度与鲁棒性。一般如果采用搜索算法进行大视场图像重建，建议采用广度优先搜索而不是深度搜索，因为深度优先搜索容易产生较大的累计误差。
2.最小生成树算法*
总体思路：将所有相邻的小视场图进行两两配准，用合适的评价算法对每次配准结果打分(比如拼接效果越好就给定更小的权值)，最后所有的连接边(成功配准上的两幅图)都有一个权值，权值越小配准效果越好。获得所有连接边和其对应权值后，只要找到一条连接路线，该路线包括了所有图像节点且路线上的权值和最小，那么可以认为按这条路线进行拼接，最后结果最优。这个查找最小权值路线的算法就是最小生成树算法。
关于最小生成树算法的介绍与实现，这篇文章写的很详细，有需要的可以参考。
可惜的是，不论对图像配准还是点云配准，都没有十分有效的评价方法来评价配准的效果，评价结果只能保证大致正确，有时并不值得信赖。这里简单补充一下常用的评价方法，对于图像配准评价可以用互相关值大小作为评价指标，对于点云配准可以用最近邻点欧式距离和大小作为评价指标(仔细想想可以发现其实最近邻欧式距离和可以算作点云的互相关值大小)。
最小生成树算法需要专门设置配准评价方法进行打分，而且需要保证评价方法大致有效(大致有效主要指能够一定程度区分不同配准的结果好坏)。最小生成树算法在评价方法还OK的情况可以避开错误配准的边，选择那些配准效果更好的边进行大视场图像重建。但是它也没有解决误差累计这个问题。
3.全局捆绑调整算法
假设以第一张图像的坐标系为全局坐标系，计算其他每张节点图像(小视场图像)到全局坐标系下的坐标变换，如下图所示，即求解每个节点图像在全局坐标系下的坐标。（这个问题与SLAM中求解相机姿态的图后端优化是一样的，实际上它是相机位姿优化的简化版了，不需要进行投影，单个节点的变量也仅x,y两个）
这个优化求解方法采用的就是捆绑调整(BA)，下面我简单介绍一下全局BA是如何求解每个图像节点位置坐标的。
首先明确一下已知量和需要求解的变量，已知量是经过两两配准后得到的两幅图像节点的变换关系，也即下图中没有打红叉的连接边，需要求解的变量即下图中15个图像节点的全局坐标。那么怎样求解这个问题呢？
我们先来看图像节点0和节点1，假设节点0到节点1的变换为z1(通俗点说也就是将图0与图1进行配准，图1相对图0在水平和竖直方向上的位移为(a1,a2)，用z1表示)，图像节点0的全局坐标为h0，节点1的全局坐标为h1那么就有：
e 1 = （ h 1 − h 0 ） − z 1 e_1 = （h_1 - h_0） - z_1 e1=（h1−h0）−z1
e1表示误差大小。
那么我们对所有连接边计算误差，求和：
m i n F ( h 0 , h 1 , . . . h k , . . . h 15 ) = ∑ i = 1 n ∣ ∣ e k ∣ ∣ minF(h~0~, h~1~, ...h~k~, ...h~15~) = \sum_{i=1}^{n} ||e_k|| minF(h 0 ,h 1 ,...h k ,...h 15 )=∑i=1n∣∣ek∣∣
使得误差和
F
F
F达到最小的
h
0
,
h
1
,
.
.
.
h
k
,
.
.
.
h
15
h_0, h_1, ...h_k, ...h_{15}
h0,h1,...hk,...h15即为所求。
这是一个非线性优化问题，常用的求解算法有：最速下降法、Gauss-Newton法、Levenberg-Marquadt法等。所幸的是上述过程包括求解非线性优化问题，我们都可以用g2o框架轻松实现。
如果对上述过程不是很清楚的，可以参考深入理解图优化。
全局捆绑调整算法可以很好的消除拼接过程中的累计误差，但是认真想一想会发现它求取的是全局最优解（总误差和最小），那么当配准结果中存在配准错误，这个错误所产生的影响将被分配到每个图像节点中去，对于高分辨率拼图来说这个问题是不能忍受的（可以想一想，当其他所有边都配准正确，唯独有一条边配准错误，那么当他的错误被分配到其他正确的结果中去，虽然总体上误差小了，但是那些正确的配准结果都会产生一定的偏离，这就像一颗老鼠屎坏了一锅汤）。所以如果拼图对分辨率要求不高，或者配准算法有比较好的鲁棒性，可以考虑采用全局BA。
4.全局调整与回路检测算法*
全局调整算法可以解决累计误差的影响，那么只要想办法剔除那些错误的配准结果，再进行全局调整，是不是就能获得一个比较好的结果呢？那到底怎样才能剔除这些错误的配准结果呢？
首先我们应当有一个共识：配准错误的连接边
i
i
i 在和其他边一起进行全局BA后，其误差
e
i
e_i
ei 仍然会明显大于其他边的误差
e
k
e_k
ek ,并且越靠近该连接边的其他连接边受到的影响也越大（还是老鼠屎的例子，越靠近老鼠屎的汤，老鼠屎溶液的浓度也会越高），那么我们可以选取一个阈值T，将那些误差
e
1
.
.
.
e
n
e_1...e_n
e1...en 大于T的边取出，这些边中就存在错误配准的边。于是我们获得了正确配准边的边集
E
1
E_1
E1 ，和包含了错误配准边和正确配准边的边集
E
2
E_2
E2 。
那么边集
E
2
E_2
E2里面到底哪些是错误配准的边，哪些是被影响的边呢？这里我们就要用到回路检测了。对边集
E
2
E_2
E2中的每条边，我们都去边集
E
1
E_1
E1中寻找能与其构成最小回路的边，比较最小回路所构成的变换关系和这条边所代表的变换关系（也就是配准结构啦）的误差大小，如果误差小于阈值T，则认为该边不存在配准错误，并移入边集
E
1
E_1
E1 。对误差大于阈值T的边，则用最小回路的变换关系替换这条边的变换关系。
最后我们只需要对更新后的变换关系再次进行全局BA，并不断迭代上述过程，直到
E
2
E_2
E2为空，或达到指定迭代次数为止。详细具体的实现方法可以参考文献。
该算法可以消除累计误差，剔除错误配准结果，但是还是要求所有相邻图像节点的配准正确率尽量高一些，我在做拼图的过程中，算法的配准成功率比较低的时候，很多边找不到最小回路，这时候迭代过程就会难以进行下去。
总结
一般来说，采用最小生成树算法简单有效，但是需要有一个较为有效的评价方法。而全局调整与回路检测算法实现起来较为繁琐，且在配准率不高的情况下也难以求解最优解。
附源码（最小生成树+全局调整与回路检测算法+项目地址）
最小生成树（c++）
//*******************最小生成树的拼接路径优化*****************
MatrixXf DistanceMatrix = MatrixXf::Ones(n, n);
DistanceMatrix = DistanceMatrix * MyMax;
for (list< UnitInfo >::iterator iter = StitchInfo.begin(); iter != StitchInfo.end(); iter++) {
DistanceMatrix((*iter).order.first, (*iter).order.second) = (*iter).eularDis;
DistanceMatrix((*iter).order.second, (*iter).order.first) = (*iter).eularDis;
}
list<int> MyTree;
vector<pair<float, float>> MyTreeDis;
int startPoint = 0;
MyTree.push_back(startPoint);
MyTreeDis.push_back(make_pair(0, 0));
for (int i = 0; i < n-1; i++) {
float minV = MyMax;
int currentPoint;
int nestPoint;
for (list<int>::iterator iter = MyTree.begin(); iter != MyTree.end(); iter++) {//最小生成树（Prim算法）
for (int j = 0; j < n; j++) {
bool flag = true;
for (list<int>::iterator iter_2 = MyTree.begin(); iter_2 != MyTree.end(); iter_2++) {
if ((*iter_2) == j)
flag = false;
}
if ( flag && minV > DistanceMatrix((*iter), j)) {
minV = DistanceMatrix((*iter), j);
currentPoint = (*iter);
nestPoint = j;
}
}
}
MyTree.push_back(nestPoint);
for (list< UnitInfo >::iterator iter = StitchInfo.begin(); iter != StitchInfo.end(); iter++) {
if (currentPoint < nestPoint) {
if (make_pair(currentPoint, nestPoint) == (*iter).order)
MyTreeDis.push_back(make_pair((*iter).xy_move.first + MyTreeDis[i].first, (*iter).xy_move.second + MyTreeDis[i].second));
}
else {
if (make_pair(nestPoint, currentPoint) == (*iter).order) {
MyTreeDis.push_back(make_pair(-(*iter).xy_move.first + MyTreeDis[i].first, -(*iter).xy_move.second + MyTreeDis[i].second));
}
}
}
}
//************根据相对位置关系统一点云坐标系*****************
if (access(SavePath.c_str(), 0) == 0) remove(SavePath.c_str());
int j = 0;
for (list<int>::iterator iterlist = MyTree.begin(); iterlist != MyTree.end(); ++iterlist, j++) {
point_RW RWriter_all;
Result ThisImage = RWriter_all.point_Read(Files.at(*iterlist));
float(*point)[M_Nano] = (float(*)[M_Nano]) ThisImage.pointData;
//cout << *iterlist<<"\t"<< MyTreeDis[j].first << "\t" << MyTreeDis[j].second << endl;
for (int i = 0; i < ThisImage.Num; i++) {
point[i][0] = point[i][0] + MyTreeDis[j].first;
point[i][1] = point[i][1] + MyTreeDis[j].second;
}
Result DataP;
DataP.pointData = (float(*)) ThisImage.pointData;
DataP.Num = ThisImage.Num;
RWriter_all.point_Write(DataP, SavePath);
delete ThisImage.pointData;
}
全局调整与回路检测算法(matlab)
%全局路径优化
%Reference：
%[1]岳永娟, 苗立刚, 彭思龙. 大规模显微图像拼接算法[J]. 计算机应用, 2006, 26(5):1012-1014.
%[2]苗立刚, 岳永娟, 彭思龙. 显微图像拼接的误差分析[J]. 小型微型计算机系统, 2007(07):1255-1258.
clear all;close all;clc
global Image_width;
global Image_length;
global Num;
global edge;
Image_width = 5;
Image_length = 5;
Num = Image_width*Image_length;
ThreError = 10;%全局对准误差的阈值
iterNum = 20;
saveFile = 'C:\Users\Mr Xin\Desktop\MovingFile.txt';
%% Step1 计算局部对准参数，并剔除可靠性低的边
% [Matrix_AX, Matrix_AY]= stitchPara(Image_width, Image_length);%构造拼接局部参数矩阵
% save('Matrix_A','Matrix_AX','Matrix_AY');
load('Matrix_A');
[edgeRow, edgeColumn]=find(Matrix_AX~=0);%计算去除大误差后的连接边
edge = [edgeRow, edgeColumn];
A=HessianMatrix();%构造Hessian Matrix
emptyList = [];
for i = 1:Num
if A(i,:)==zeros(1,Num)
emptyList = [emptyList,i];
end
end
for iter = 1:iterNum
%Step2 计算全局对准参数
[b_X, b_Y]= b_VectorGet(Matrix_AX, Matrix_AY);
global_X = -inv(A)*b_X;
global_Y = -inv(A)*b_Y;
% Step3 计算全局对准误差并将边集分类
EdgeSize = size(edge,1);
ErrorValue = zeros(EdgeSize,2);
for i=1:EdgeSize
ErrorValue(i,1) = (abs(global_X(edge(i,2)) - global_X(edge(i,1))) - abs(Matrix_AX(edge(i,1),edge(i,2))))^2+...
(abs(global_Y(edge(i,2)) - global_Y(edge(i,1))) - abs(Matrix_AY(edge(i,1),edge(i,2))))^2;
if ErrorValue(i,1)>=ThreError
ErrorValue(i,2)=0;
else
ErrorValue(i,2)=1;
end
end
E1 = edge(ErrorValue(:,2)==1,:);%误差较小的边
E2 = edge(ErrorValue(:,2)==0,:);%误差较大的边
if isempty(E2)
break
end
% Step4 最小回路消除误差
N1 = size(E2,1);
A_Dijkstra = A;
A_Dijkstra(E2(:,1),E2(:,2)) = inf;
A_Dijkstra(A_Dijkstra==0) = inf;
A_Dijkstra(logical(eye(size(A_Dijkstra)))) = 0;
A_Dijkstra(A_Dijkstra==-2) = 1;
for i=1:N1%更新局部参数矩阵
tempX = 0;
tempY = 0;
MinRoud = Dijkstra(A_Dijkstra,E2(i,:));
for j = 1:length(MinRoud)-1
tempX = Matrix_AX(min(MinRoud(j),MinRoud(j+1)),max(MinRoud(j),MinRoud(j+1))) + tempX;
tempY = Matrix_AY(min(MinRoud(j),MinRoud(j+1)),max(MinRoud(j),MinRoud(j+1))) + tempY;
end
ErrorValue2 = (tempX-Matrix_AX(E2(i,1), E2(i,2)))^2 + (tempY-Matrix_AY(E2(i,1), E2(i,2)))^2;
if ErrorValue2>ThreError
Matrix_AX(E2(i,1), E2(i,2)) = tempX;
Matrix_AY(E2(i,1), E2(i,2)) = tempY;
A_Dijkstra(E2(i,1),E2(i,2)) =1;
end
end
end
save(saveFile,'global_X','global_Y','-ascii');
function [b_X, b_Y]= b_VectorGet(Matrix_AX, Matrix_AY)%获取向量b
global Num;
global Image_width;
global Image_length;
global edge;
b_X = zeros(Num,1);
b_Y = zeros(Num,1);
for i=0:Num-1
x = mod(i,Image_width);
y = fix(i/Image_width);
x1 = x-1;%四周的图序号
y1 = y;
x2 = x;
y2 = y-1;
x3 = x+1;
y3 = y;
x4 = x;
y4 = y+1;
n1 = Image_width*y1+x1;
n2 = Image_width*y2+x2;
n3 = Image_width*y3+x3;
n4 = Image_width*y4+x4;
inEdge1 = ismember([n1+1,i+1],edge,'rows');
inEdge2 = ismember([n2+1,i+1],edge,'rows');
inEdge3 = ismember([i+1,n3+1],edge,'rows');
inEdge4 = ismember([i+1,n4+1],edge,'rows');
alfa_inX = 0;
alfa_miX = 0;
alfa_inY = 0;
alfa_miY = 0;
if inEdge1 && x1>=0 && y1>=0 && x1<Image_width && y1<Image_length, alfa_miX =alfa_miX+Matrix_AX(n1+1,i+1);end
if inEdge2 && x2>=0 && y2>=0 && x2<Image_width && y2<Image_length, alfa_miX =alfa_miX+Matrix_AX(n2+1,i+1);end
if inEdge3 && x3>=0 && y3>=0 && x3<Image_width && y3<Image_length, alfa_inX =alfa_inX+Matrix_AX(i+1,n3+1);end
if inEdge4 && x4>=0 && y4>=0 && x4<Image_width && y4<Image_length, alfa_inX =alfa_inX+Matrix_AX(i+1,n4+1);end
b_X(i+1,1) = alfa_inX - alfa_miX;
if inEdge1 && x1>=0 && y1>=0 && x1<Image_width && y1<Image_length, alfa_miY =alfa_miY+Matrix_AY(n1+1,i+1);end
if inEdge2 && x2>=0 && y2>=0 && x2<Image_width && y2<Image_length, alfa_miY =alfa_miY+Matrix_AY(n2+1,i+1);end
if inEdge3 && x3>=0 && y3>=0 && x3<Image_width && y3<Image_length, alfa_inY =alfa_inY+Matrix_AY(i+1,n3+1);end
if inEdge4 && x4>=0 && y4>=0 && x4<Image_width && y4<Image_length, alfa_inY =alfa_inY+Matrix_AY(i+1,n4+1);end
b_Y(i+1,1) = alfa_inY - alfa_miY;
end
end
function A=HessianMatrix()
global Num;
global Image_width;
global Image_length;
global edge;
A=zeros(Num,Num);
for i=0:Num-1
d = 0;
x = mod(i,Image_width);
y = fix(i/Image_width);
x1 = x-1;%四周的图序号
y1 = y;
x2 = x;
y2 = y-1;
x3 = x+1;
y3 = y;
x4 = x;
y4 = y+1;
n1 = Image_width*y1+x1;
n2 = Image_width*y2+x2;
n3 = Image_width*y3+x3;
n4 = Image_width*y4+x4;
inEdge1 = ismember([n1+1,i+1],edge,'rows');
inEdge2 = ismember([n2+1,i+1],edge,'rows');
inEdge3 = ismember([i+1,n3+1],edge,'rows');
inEdge4 = ismember([i+1,n4+1],edge,'rows');
if inEdge1 && x1>=0 && y1>=0 && x1<Image_width && y1<Image_length
A(n1+1,i+1)=-1;
A(i+1,n1+1)=-1;
d = d+1;
end
if inEdge2 && x2>=0 && y2>=0 && x2<Image_width && y2<Image_length
A(n2+1,i+1)=-1;
A(i+1,n2+1)=-1;
d = d+1;
end
if inEdge3 && x3>=0 && y3>=0 && x3<Image_width && y3<Image_length
A(i+1,n3+1)=-1;
A(n3+1,i+1)=-1;
d = d+1;
end
if inEdge4 && x4>=0 && y4>=0 && x4<Image_width && y4<Image_length
A(i+1,n4+1)=-1;
A(n4+1,i+1)=-1;
d = d+1;
end
A(i+1,i+1) = d;
end
end
function MinRoud = Dijkstra(A_Dijkstra,E2)%搜索最小回路
A_Dijkstra = A_Dijkstra+A_Dijkstra';
pb(1:length(A_Dijkstra))=0;pb(E2(1,1))=1; %当一个点已经求出到原点的最短距离时，其下标i对应的pb(i)赋1
index1=1; %存放存入S集合的顺序
d(1:length(A_Dijkstra))=inf;d(E2(1,1))=0; %存放由始点到第i点最短通路的值
temp=E2(1,1); %temp表示c1,算c1到其它点的最短路。
while sum(pb)<length(A_Dijkstra) %看是否所有的点都标记为P标号
tb=find(pb==0); %找到标号为0的所有点,即找到还没有存入S的点
d(tb)=min(d(tb),d(temp)+A_Dijkstra(temp,tb));%计算标号为0的点的最短路，或者是从原点直接到这个点，又或者是原点经过r1,间接到达这个点
tmpb=find(d(tb)==min(d(tb))); %求d[tb]序列最小值的下标
temp=tb(tmpb(1));%可能有多条路径同时到达最小值，却其中一个，temp也从原点变为下一个点
pb(temp)=1;%找到最小路径的表对应的pb(i)=1
index1=[index1,temp]; %存放存入S集合的顺序
if ismember(E2(1,2),index1)
MinRoud = index1;
break;
end
end
end
另附点云拼接的项目地址，配准采用JRMPC算法，大视场拼接采用了最小生成树。
https://github.com/zc-fly/zc-fly-2DPointCloud_Reconstruction
4286
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
