GKR协议学习

参考资料：Justin Thaler 的 《Proofs, Arguments, and Zero-Knowledge》

在GKR协议需要以下预备知识：

1. 求和验证Sumcheck协议

2. 多线性扩展

3.GKR协议中最重要的引理:

证明上述引理的逻辑：

1. 等式左边  是的多线性扩展。
2. 如果等式右边是关于的多线性多项式且在的值都等于，那么根据多线性扩展定义，是的多项式扩展。
3. 最终，根据多线性扩展的唯一性有

书中具体的定理证明如下：

        显然，由于和是多线性多项式，那么等式右边是关于z的多线性多项式。对于任意的门，并假设a是电路的第i层的加法门，加法门a的两个输入记为和。最终有，

由于a是加法门，那么任意乘法门对应的乘法函数有

最终得到如下等式：

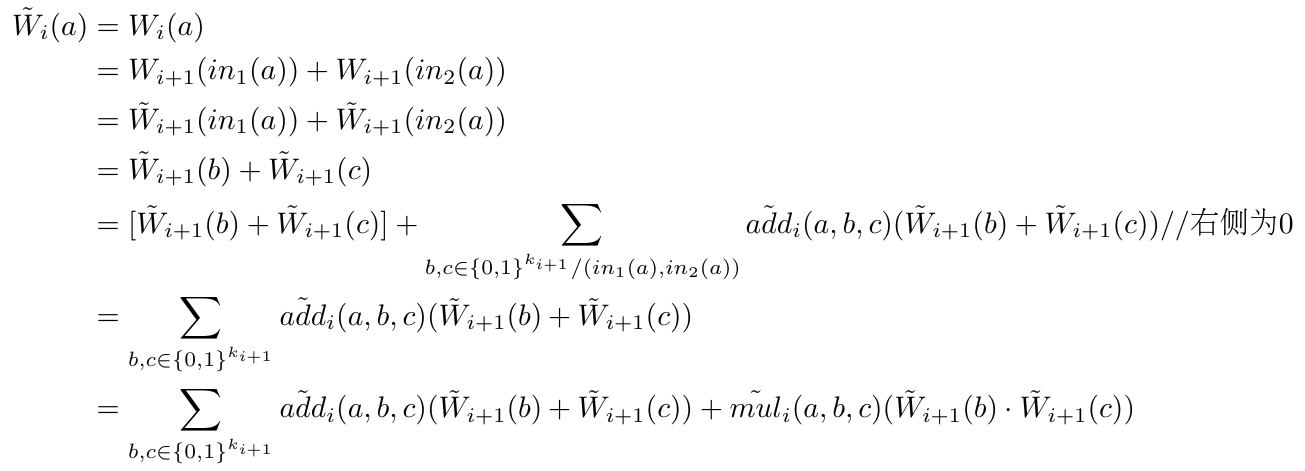
将a替换成z,最终完成引理的证明。                                                         

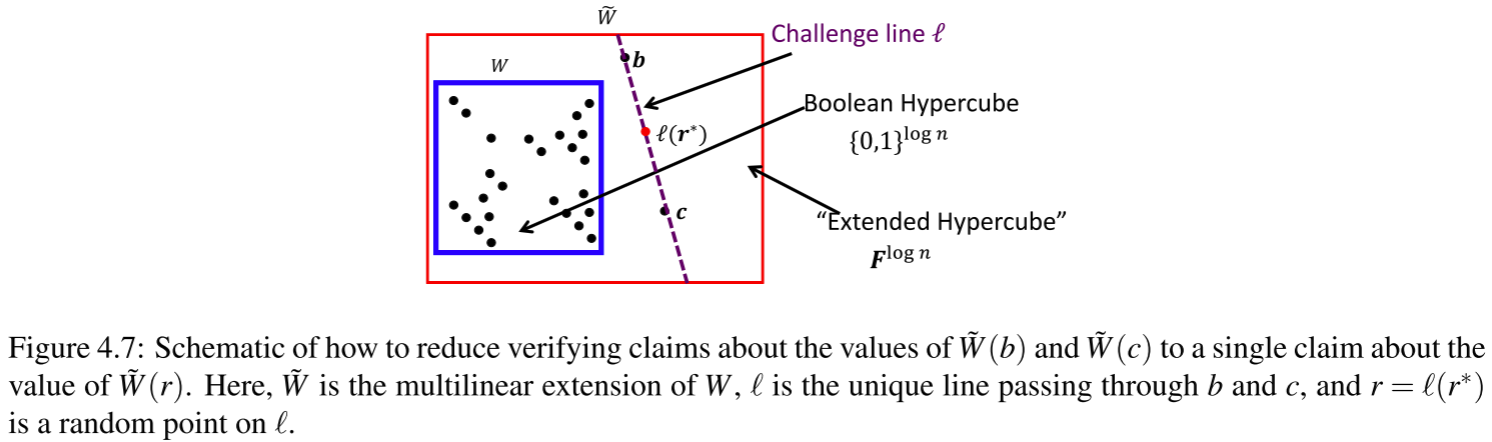
4.子协议：多点多项式计算归约到单点计算 (书中4.5.2节）

        在协议中会反复将求和验证Sumcheck协议作为子协议，因此在Sumcheck协议中的最后一步验证者Verifier去计算函数在多个点的值，从而完成验证。如果进行反复计算，一方面提高了Verifier的计算开销，另一方面还需要进行交互。因此，我们希望由证明者Prover去做多点多项式计算，Verifier只需验证Prover是否诚实地在某些点上的计算。

        首先，假设是域F上的元多线性多项式，验证者希望多项式只在计算多项式值。我们介绍了一个简单的一轮交互证明，其通信成本为O(logn)，它将和的计算降低为单点计算。这意味着协议将强制证明者P发送和的声明值v0和v1，以及验证者V以特定方式选择的许多其他点的声明值。然后验证者V将从这些点中随机选择r，并且只要P关于的断言有效，V就可以高概率地相信和。

        该协议可以应用于无向图中计数三角形的Sumcheck协议的末尾， 等于 ，以减少验证者V需要计算 在三个点的时间，并从3个点减少到一个点。由于这些计算是V运行时的主要成本，因此这基本上将V的时间减少了3倍。

---

5.GKR协议

        GKR协议是一个交互式证明IP的通用协议，但不是论证协议也不是一个零知识证明协议。

        GKR协议应用在d层，扇入为2，输入的层级算术电路。令，其中表示电路的第i层门的数量，门的编号从0到-1。电路的每一层都可以用函数来表示，将门的二进制编号映射到门的输出。

         协议的最开始，证明者发送函数，并声称其等于，也就是电路的输出。要证明这两个函数相等，我们使用多线性扩展+Schwartz–Zippel引理来证明。因此之后，验证者随机选取，并计算。之后，证明者需要向验证者证明的剩余部分就是。

        当i=0，即第0层时，定义个元的多元多项式

由引理可得

 因此Prover需要向Verifier证明：

 这是一个和形式，因此可以使用Sumcheck协议。验证者在Sumcheck协议的最后需要随机选取，并计算

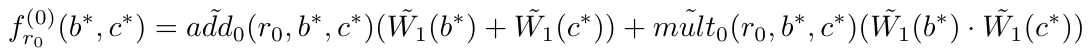。因此验证者需要计算，。 验证者可以在本地快速计算以及，这两个函数只跟电路模式有关，而跟输出的值没有关系。

        为了将函数在两点计算归约到单点计算并计算。协议调用第3节的子协议。首先，证明者设置一个线性函数并满足以及。证明者发送，验证者计算，作为的值。最后，验证者随机选取，设置以及。因此，验证者最后可以计算，完成Sumcheck协议。然而， 根据子协议而言需要证明。因为在子协议中验证者知道函数，而在GKR协议中验证者是不知道函数。因此接下来会进行一个循环，直到第d层证明。由于是输入函数的多线性扩展，因此验证者知道该函数，从而可以验证是否相等，最终完成GKR协议。

        可以看出，子协议在完成上下两层的Sumcheck协议的同时，将上层的claim归约到下层的claim。

GKR协议的可靠性来自Sumcheck的可靠性以及子协议多点计算归约到单点计算的可靠性。