On the Size of Pairing-based Non-interactive Arguments 论文学习笔记

符号

证明者 prover

验证者 verifier

语句 statement

证据 witness

简洁非交互论证 SNARGs

简洁非交互知识论证 SNARKs

非交互式零知识证明 NIZK

公共参考字符串  CRS

次线性 sublinear

二次算术程序 QAP

二次张成程序 QSP

布尔电路可满足性问题 boolean-SAT

算术电路可满足性问题 arithmetic-SAT

指数知识假设  KEA

---

摘要

        非交互论证使证明者说服一个验证者相信某个语句是真的。近年来，在构建小尺度、低验证复杂度的高效非交互论证，即简洁非交互论证(SNARGs)和简洁非交互知识论证(SNARKs), 在理论和实践上都取得了很大的进展。

       许多SNARGs方案的构造依赖于配对密码学。在这些构造中，一个证明由多个群元素构成，验证等式则由多个配对乘积等式组成。本文中要解决的问题是基于配对的SNARGs如何高效运行。

       第一个贡献是基于配对(预处理)的算术电路可满足性SNARK，算术电路可满足性是一种NPC语言。在该SNARK中，我们使用了非对称配对来提高效率，一个证明仅有3个群元素，而验证使用3个配对运算来检验一个配对的乘积等式。我们的SNARK是零知识的没有透露任何关于证明者的证据。

       第二个贡献，我们回答了[BCI+13]提出的一个开放问题，即2轮线性交互证明不具有线性决策过程。由此可见，证明者和验证者使用通用非对称双线性群操作的SNARGs不能由单个群元素组成。这给出了基于配对的SNARGs的第一个下界。这个下界是否可以扩展到排除2个群元素的SNARGs，仍然是一个有趣的开放问题，这将证明3个元素结构的最优性。

关键字：SNAKRs, 非交互零知识论证，线性交互证明，二次算术程序，双线性配对。

---

1.引言

 Goldwasser、Micali和Rackoff [GMR89]引入了零知识证明，使证明者能够说服验证者相信某个语句是真的，而不泄露其他任何东西。它们有三个核心属性:

• 完备性：给定一个语句以及一个证据，证明者能够使验证者相信这是一个真的语句。
• 可靠性：一个恶意的证明者不能说服验证者相信某个为假的语句。
• 零知识性：在整个证明中除了泄露语句是真的外，不泄露其他任何保密的东西，特别是不泄露证明者的语句。

        Blum, Feldman和Micali [BFM88]将零知识概念扩展到公共参考字符串模型(CRS)中的非交互式零知识证明(NIZK)。NIZK在非交互式密码方案的构造中是有用的，例如数字签名和CCA-secure公钥加密。(数字签名比如Schnorr签名，用在CCA-secure公钥加密就不太清楚了）

        通信量是零知识证明的一个重要性能参数。[Kil92]给出了第一个次线性通信大小的零知识论证，该论证发送的比特数小于待证明语句的大小。[Mic00]通过让证明者在一个高效通信论证中使用密码函数计算验证者的挑战 ，最终构造了次线性大小的论证。正如Kilian [Kil95]所述，当交互参数是公共硬币(public coin) 以及零知识时，实现了次线性大小的NIZK证明。 

        Groth, Ostrovsky和Sahai [GOS12,GOS06,Gro06,GS12]引入了基于配对的NIZK证明，产生了第一个基于标准假设的线性大小证明。[Gro10]将这些技术与交互的零知识论证[Gro09]的思想相结合，给出了第一个常量大小的NIZK论证。[Lip12]使用了一种基于无进程集的替代结构来减少CRS的大小。

        Groth的常数大小NIZK论证是基于构造一组多项式方程，并使用配对来有效地验证方程。[GGPR13]找到了一个基于拉格朗日插值多项式的多项式方程的深刻构造，并产生了一个基于配对的NIZK论证。该论证的CRS大小与语句和证据的大小成比例。[GGPR13]给出了两类多项式方程:布尔电路可满足性的二次张成程序(QSP)和算术电路可满足性的二次算术程序(QAP)。[Lip13]提出使用纠错码(error correcting codes)构建更高效的QAP，[DFGK14]将QSP改进为平方张成程序(SSP)，并给出由4个群运算构成的boolean-SAT的NIZK论证。

        随着理论进展[PHGR13,BCG+13,BFR+13,BCTV14b,KPP+14,BBFR15,CTV15,

WSR+15,CFH+15,SVdV16]，零知识证明高效工作令人兴奋。最高效的实现进一步理解了[GGPR13]的二次算术程序方法，然后将其与编译器结合，生成合适的二次算术程序，该程序与证明的语句等价; libsnark [BCTV14b,BSCG+14]也包含一个基于[DFGK14]的NIZK论证。

        构建高效非交互式论证的一个有力动机是可验证计算(VC)。客户端将一个复杂的计算任务外包给服务器，服务器将结果返回给客户端。为了使客户端相信计算结果是正确的，服务器可能会在返回结果中包含一个非交互式论证的证明。但是，由于验证者并没有很多的计算资源，这只有在论证紧凑且验证计算量小的情况下才有意义，即该论证是一个简洁的非交互论证(SNARG)或一个简洁的非交互知识论证(SNARK)。虽然基于配对的SNARG对验证者来说是高效的，但对证明者来说，计算开销仍然太高，不足以保证在外包计算中使用[WB15,Wal15]，还需要进一步提高效率。目前情况，zk-SNARKs已经在证明关于隐私数据的语句中发挥了作用。例如，zk-SNARKs是虚拟货币提案匹诺曹币[DFKP13]和零钞[BCG+14]的关键组成。

        与基于配对的NIZK论证的研究并行的是有关理解SNARKs方面。[GW11]证明了SNANGs必须依赖于非证伪假设，[BCCT12]证明当且仅当存在可提取的抗碰撞哈希函数存在时，指定验证者SNARKs才存在。在效率方面，特别有趣的是一系列研究SNARKs如何组成的工作[Val08,BCCT13,BCTV14a]。它们向我们展示了一个含有较长CRS的preprocessing SNARK可以构建一个含有较短CRS的完全简洁SNARK。

        [BCI+13]给出了一个依靠域元素线性编码的SNARKs抽象模型。[BCI+13]的信息论框架称为线性交互证明(LIPs)，capture证明系统中证明者只能通过线性操作来计算她的消息。他们使用配对技术将2轮的LIP转换为可公开验证的SNARK或者使用加法同态将其转换为指定的验证者的SNARK。

1.1我们的贡献

Succinct NIZK.

        我们构造了仅由3个群元素证明的arithmetic-SAT的NIZK论证。这个证明小且容易验证。验证者只需要计算与语句大小成比例的指数运算，并验证只有3个配对的单个配对乘积方程。我们的构造可以用任何类型的配对实例化，包括type III配对，这是最有效的配对。

        该论证具有完全完备性和完美零知识。对于可靠性，我们采取了积极的观点以及依赖于通用双线性群模型[Sho97,Nec94]中的安全性证明来获得最佳性能。这种观点在一定程度上得到了[GW11]的支持，他们基于标准的可证伪假设排除了SNARG。但是，在[AGOT14]之后，通过证明构造在对称配对设置中是安全的来抵抗了密码分析。为了获得最佳效率，在非对称通用群中使用NIZK论证是有意义的，然而，通过在对称设置中提供安全性证明，我们获得了额外的安全性:即使密码分析的进展产生了迄今为止未知的源群之间的有效可计算同构，这并不一定会导致我们的方案的中断。因此，我们有一个统一的NIZK论证，可以用任何类型的配对实例化，产生最优的效率和最优的通用双线性群体弹性。

        表1给出了boolean-SAT的性能比较，表2给出了arithmetic-SAT的性能比较，分别是CRS的大小、证明的大小、证明者的计算量、验证者的计算量以及用于验证一个证明的配对乘积方程的数量。在所有的效率参数上，我们的工作表现都优于目前的技术水平。

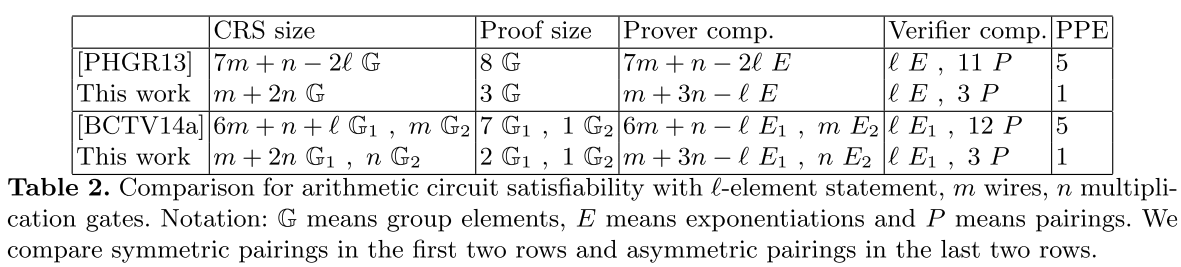
       由于每个门都有输出线， 所以线的数量会超过门的数量 。一般情况下，语句的大小会比线的数量和门的数量都少。在两个表中，我们没有给出的关系的大小。在boolean-SAT的情况下，考虑任意扇入为2的逻辑门。在arithmetic-SAT的情况下，考虑使用扇入为2的乘法门，其中每个输入因子可以是其他导线的加权和。我们假设每个乘法门输入依赖于固定数量的导线;否则，计算关系本身的代价可能会超过生成证明的代价。[PHGR13]使用了对称双线性群G1 = G2，因此我们也将所构造的方案使用对称双线性群来实例化在进行比较。 [PHGR13]在CRS中保存了n个群元素。但是，[PHGR13]方案使用非对称群的效率更高。

证明大小的重要性

        虽然将证明的大小减少到3个群元素和验证时间的减少本身很nice，但我们想要强调的是，这在编译成SNARKs时是尤为重要。[BCCT13,BCTV14a]表明预处理SNARKs与一个长的CRS可以组合成fully succinct  SNARKs与一个短的CRS。这个转换将语句分解成更小的部分，证明每一部分本身是正确的，并递归地构造其他证明的知识证明，这些证明共同表明这些部分是正确的，并且相互吻合。在证明的递归构造中，当证明很小且易于验证时，就会有额外的好处，因为结果语句“存在一个满足验证方程的证明……“使自身变小。因此，由于SNARK的验证过程更有效，证明者的计算量更低，而且递归组合中的语句更小，这两个事实都让我们受益。Chiesa和Virza [CV16]报告了在[BCTV14a]的实现中使用我们的SNARKs达到了4-5因子的加速。

技术

        文献中所有基于配对的SNANK都遵循一个共同的范式，即证明者使用通用群操作来计算群元素，验证者使用大量配对乘积方程来验证。Bitansky等人[BCI+13]通过线性交互证明(LIPs)的定义将这种范式形式化。线性交互式证明在有限域上工作，证明者和验证者的信息由域元素的向量组成。它进一步要求证明者只使用线性操作来计算她的消息。一旦有了一个合适的2轮LIP，就可以通过配对密码学中的“指数”将其编译成SNARK。效率提高的第一个来源，设计了一个QAP的LIP，证明者只发送3个域元素。相比而言，[GGPR13,PHGR13]的QAP对应于证明者发送4个域元素的LIPs。

        与之前的工作相比，效率提高的第二个来源是对LIP的更激进的编译。[BCI+13]在对称双线性群中提出了一种变换，其中每个域元素编译成两个群元素。之后，使用指数知识假设来证明证明者知道相关的域元素。更加激进的选择是将每个域元素编译为单个群元素。每个域元素使用一个群元素编译可以提高效率，但我们只能将其证明在通用群模型上[Sho97,BBG05]，因为我们不再使用KEA。也有可能在这两个极端之间做出选择，例如[PHGR13]设计带有4个域元素的LIP，之后编译成7个群元素。总之，本文选择了最大的效率，将LIP中的每个域元素编译成一个单独的群元素，并在通用群模型中讨论安全性。

一般所说的指数知识假设指的是这个假设表明敌手一定知道某个指数c，使得。

        我们更喜欢使用非对称双线性群，因为它们比对称双线性群效率高。这意味着，除了验证者在LIP中发送的域元素数量和合适的编译选择之外，还有更多的事情要做。当使用非对称双线性群时，域元素可以作为第一个群元素、第二个群元素或两者中的指数出现。我们的LIP经过精心设计，每个域元素都被编译成一个群元素，以便将证明大小总共减少到3个群元素。

下界

        为了更高效的非交互式论证，很自然地会问最少的证明大小是多少。我们将证明基于配对的SNARGs具有单个群元素证明是不存在的。这一结果与[BCI+13]提出的一个开放性问题有关，验证者是否存在具有线性决策过程的LIPs。这样的线性决策程序是非常有用的;例如，它可以基于ElGamal加密构建SNARG。

        通过证明带有线性决策过程的LIPs不存在来否定性地回答这个开放问题。这样做的一个结果是，任何基于配对的SNARG必须将来自证明的组元素配对在一起，以使决策过程是二次的而不是线性的。因此，对于非对称双线性群，必须在两个群中都有元素才能进行配对。这排除了1个群元素SNARG的存在，无论它是否为零知识，并表明我们的NIZK论证接近最优证明大小。通过从每个群G1和G2中仅各自使用一个元素来构建一个SNARG，或者排除这样一个SNARG的存在来完全弥补这个差距，仍然是一个有趣的开放问题。

---

2.预备知识

        给定两个函数 ，当，则。若，是可忽略的。若，是压倒性的。表示一个安全参数。

2.1双线性群

双线性群具有以下性质:

• G1、G2、GT都是素数阶群。
• 配对e: G1 ×G2→GT是双线性映射。
• g是G1的生成元，h是G2的生成元，e(g, h)是GT的生成元。
• 有多个高效的算法来进行：计算群操作 ，计算双线性映射，判定群成员，判定群元素的相等性以及抽样群的生成元。我们称这些操作为通用群操作。

        双线性群的建立方法有很多种，一种是对称双线性群G1 = G2，另一种是非对称双线性群G1!= G2。[GPS08]将双线性群分为三类:

• Type I是G1 = G2，
• Type II是存在高效可计算的非平凡同态Ψ: G2→G1，
• Type III是在G1和G2之间的任意方向上都不存在高效可计算的同态。

        Type III双线性群是双线性群中最高效的一类群，因此与实际应用最相关。我们给出了Type III双线性群中基于配对的SNARGs的下界。另一方面，我们的构造可以在所有三种类型的双线性群中实例化。 

        使用一种表示元素群的离散对数的表示法是很有用的。我们强调离散对数是难计算的，这个符号只是为了便于表示。

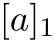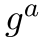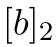• 表示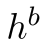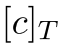，表示， 表示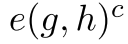。在这种表示法下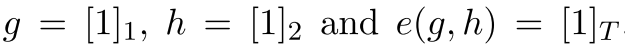，，而零元素是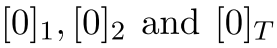。使用群的离散对数表示下，。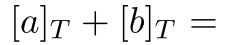
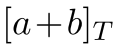• 一个群元素的向量表示为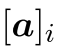。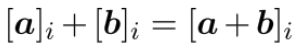表示同一个群向量的离散对数加法。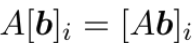表示矩阵乘以向量的群乘法。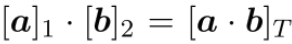表示两个群向量的配对操作。

        一个算法是通用的, 如果仅使用通用群操作来创建和操作群元素。[Sho97]考虑了随机单射编码而不是真正的群元素，从而形式化了通用群模型。通用群操作是通过一个oracle来进行访问，例如它实例化 ，则返回。由于编码的随机性，通用算法只能通过通用群oracle进行有意义的操作。这意味着，如果它有输入和返回元素，我们可以通过检查它在G1中做的加法查询有效地推导出矩阵M，使。在G2中也是如此，而在GT中也可能有从配对操作中计算出来的元素，但我们仍然可以在输入中将任何输出元素写为二次多项式。

2.2 非交互知识的零知识论证

         设是一个关系生成器，给定安全参数λ，返回一个多项式时间内可判定的二元关系。对于，称为语句(statement)，称w为证据(witness)。定义为输入为的关系R的集合。假设λ可以从R的描述中推导出来。也可以输出一些额外信息，一个辅助输入 z 提供给敌手。对于来说，一个高效可公开验证的非交互式论证是一个四元组的概率多项式算法

计算可靠性

        是可靠的，如果不可能证明一个假的语句，也就是说如果没有witness的存在可以说服验证者。设是关系R中所有存在witness的语句构成的语言, 也就是。

形式上，我们要求对于所有非一致性多项式时间敌手A有

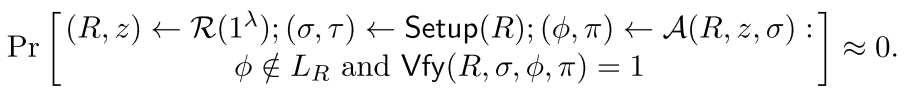
计算可靠性描述了敌手A在没有witness的输入下，产生的语句没有witness且产生的语句和证明通过验证的概率近似为0。

计算知识可靠性

        为了加强可靠性的概念，我们称是知识论证的，如果存在一个提取器，在敌手生成一个有效证明时计算出witness。提取器可以完全访问对手的状态，包括任何随机的硬币。形式上，要求对于所有非一致性多项式时间敌手A，存在一个非均匀多项式时间提取器，使得

        

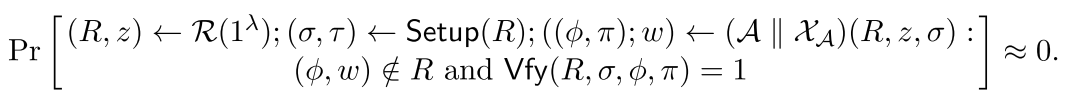
知识可靠性想说明的是：如果证明者能通过验证则代表有“知识”witness, 那么一定存在提取器能将证明者的知识提取出来。等价于如果提取器不能提取出A的知识或者说提取的“知识”是无效的，则说明恶意的证明者没有“知识”。

上述定义表明：提取器提取无效知识且通过验证的概率近似为0.

等价于 提取器提取有效知识 或 不能通过验证 的概率近似为1. 

等价于 如果通过验证，那么提取器提取有效知识 的概率近似为1.

等价于 如果提取器提取无效知识，那么不能通过验证 的概率近似为1.

证明者有知识是通过验证的必要条件。通过验证表示证明者有知识，没有通过验证表示证明者没有知识。

公开可验证和指定验证者证明

        我们将公共参考字符串σ分解为证明者使用的σP和验证者使用的σV。当σV可以从σP推导出来时，非交互论证是公开可验证的。否则，称为指定验证者论证。对于指定验证者论证，可以放宽可靠性和知识可靠性，使敌手只看到σP而看不到σV。

SNARGs 和 SNARKs. 

• 一个非交互式论证， 如果验证者运行时间为λ + |φ|的多项式以及证明大小为λ的多项式(i.e., V(time)=poly(λ + |φ|)，|π|=poly(λ)) 且具有可靠性的，称为预处理简洁非交互式论证；如果有知识可靠性，称为预处理简洁知识论证。
• 如果CRS长度也是λ的多项式(i.e.，|σ|=poly(λ)），非交互式论证是一个完全简洁的SNARG或SNARK。[BCCT13]表明预处理SNARKs可以组合产生一个完全简洁的SNARKs。本文的重点是对SNARKs进行预处理，其中公共引用字符串可能会很长。

良性关系生成器

        [BCPR14]表明，不可区分混淆意味着对于每个候选SNARK，都存在辅助输出分布，使敌手能够创建有效地证明并且不可能提取witness。假设公共硬币不同的输入混淆和其他加密假设，[BP15]强化了这种不可能性，表明存在辅助输出分布，击败了所有candidate snark的witenss提取。然而，这些反例依赖于特定的辅助输入分布。因此，在下文中，我们将假设关系生成器是良性的，因为关系和辅助输入的分布方式使得我们构建的SNARKs可以是知识可靠的。

2.3 二次算术程序

        考虑一个由有限域F上的加法和乘法门组成的算术电路。我们指定一些输入/输出来实例化一个语句，并使用电路中的其他连接来定义一个证据。这样就可以表示为一个二元关系R，由语句导线和证据导线构成的，来满足算术电路。 

        在一般化算术电路时，我们可能对于一组变量上的方程所描述的关系感兴趣。一些变量对应于语句，其余的变量对应于证据。这种关系由满足所有方程的语句和证据组成。方程总是满足，变量

 其中是上的常量，表示第q个方程。

        我们观察到加法和乘法门是上述方程的一种特殊情况，因此上述算术约束系统确实一般化了算术电路。例如，一个乘法门可以被描述为(使ui = 1, vj = 1和wk = 1,其余的都设置为0)。加法门在方程中也是容易处理的，如果, 则两边同时乘以一个。

        我们遵循[GGPR 13]中的描述，将上述算术约束系统重新表示为二次算术程序。给定n个等式，随机选取n个不同的数并定义，令是n-1次多项式，使得

        举个例子来结合R1CS理解上述的QAP。

         在实际中，关系以许多不同的方式产生。关系生成器可能是确定性的，也可能是随机的。它可能是首先生成了域F，然后其余部分建立在域F上。它也可能是多项式首先指定，然后选择一个随机域F。为了获得最大的灵活性，我们选择了与域和关系生成的确切方式无关的定义，不同的选项都可以通过适当的关系生成器来建模。

        我们将在基于配对的NIZK参数中让辅助信息aux指定一个双线性群。将双线性群作为关系生成器的一部分似乎有点令人惊讶，但这提供了一个更好的设置模型，其中关系是建立在一个已经存在的双线性群之上的。同样，这个选择也不失一般性，我们可以把一个传统的设置想象成，首先选择关系，然后随机选择双线性群，作为一个特殊的情况，关系生成器分两步工作，首先选择关系，然后随机选择一个双线性群。当然，让关系生成器选择双线性群是我们需要假设它是良性的另一个很好的理由; 双线性群的合理选择是保证安全的关键。

2.4 非交互式线性证明

         [BCI+13]给出SNARK构造中信息论基础的一个有用的characterization，称为2轮代数输入无关的线性交互证明。为了进一步理解2.2节定义的NIZK，我们将这个概念重命名为非交互式线性证明(NILP)。NILP是相对于关系生成器来定义的，假设指定了有限域F，具体如下。

在仿射证明者策略下统计知识可靠性

        如果能从一个成功证明的矩阵中提取一个witness，那么NILP对于仿射证明者策略具有知识可靠性。更准确地说，存在一个多项式时间提取器X，使得对敌手A有

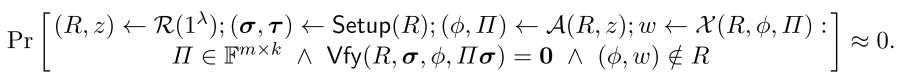
上述概率换句话说，敌手A产生的语句和矩阵不能通过验证(也就是敌手A没有witness），则多项式时间提取器X产生的witness也是无效的（也就是提取的witness是无效的）。如果敌手A产生的语句和矩阵能通过验证(也就是拥有某个witness)，则提取器能够计算出有效的witness。

2.2节中的零知识概念也适用于NILP也适用于2轮LIP的诚实验证器零知识。另一个扩展是指定验证者的NILPs，其中公共参考字符串σ被分成两部分:被证明者使用的和验证者使用的。

2.5 将线性非交互式证明改为非交互式论证

        NILP非常有用，因为可以使用双线性配对将其编译公开可验证的非交互论证，也可以使用Paillier加密的变体[BCI+13]编译成指定验证者的非交互论证。在配对操作的情况下，直觉上是一个具有两个验证者的“在离散对数中”执行的NILP。σ包含域元素的编码。证明者将证明作为CRS中群元素的线性组合来计算。验证者通过验证多个配对运算来检查论证，这对应于检查编码域元素中的二次方程。现在我们将正式介绍这种方法。

        在使用Type III配对时，“在离散对数中”执行的NILP要求为每个元素指定的运算群。因此，我们定义分裂的NILP，在分裂NILP中，一个CRS分裂成和一个证明分裂成。证明的每一部分都是从CRS的相应部分计算出来的。最后，在验证证明时我们希望验证者的检验是一个二次方程，其中每个变量的度数都是1。一个分裂NILP是具有如下形式的NILP:

        直觉上，在编译成分裂NILP后，我们希望通用群操作的作弊证明者不会偏离NILP，从而证明分裂NILP可靠性。但是，当证明者看到CRS时，可能会从中学到有用的信息，并根据学到的信息来选择矩阵。为了抵抗这样的敌手，我们定义一个无泄漏(disclosure-free)的CRS。无泄漏的CRS表明证明者没有从CRS获取有用信息来帮助她选择一个特殊矩阵。

定义4（无泄漏NILP）一个分裂NILP是无泄漏的，如果对于所有敌手A有

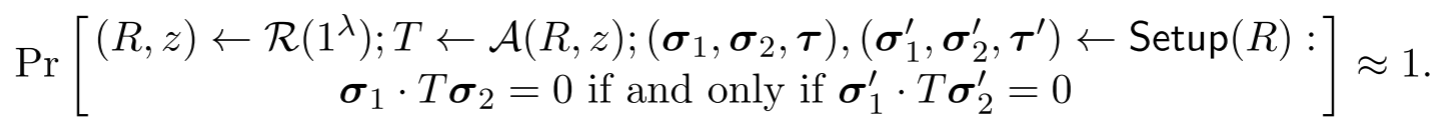
        一个解释上述无泄漏CRS定义的方法是，敌手A在σ1、σ2上运行的任何测试结果都可以通过在独立生成的σ1'、σ2'上运行来预测。

        我们现在可以描述一个编译器：将一个分裂NILP编译成一个基于配对的非交互式论证

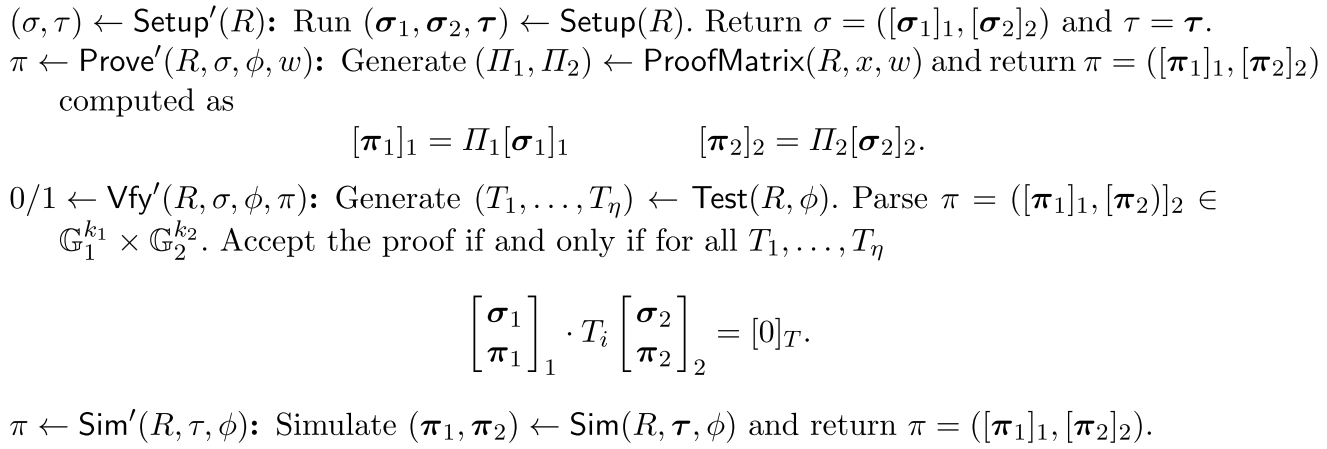
引理1. 上述基于配对的非交互式论证具有完美完备性和抵抗多项式查询的通用群敌手的统计知识可靠性。如果一个分裂的NILP是完美零知识，那么上述基于配对的非交互式论证也是完美零知识。

证明：完美完备性和完美零知识来自于NILP的完美完备性 和完美零知识。因此我们只需要证明抵抗通用群敌手的统计知识可靠性。通用群敌手使用通用群来操作G1、G2和GT中的元素，包括配对元素，判定群元素以及测试两个元素是否相等。我们首先论证无泄漏意味着敌手以可忽略的概率去学习CRS的重要信息。

        当敌手使用通用群操作来测试一个元素是否为0时，可以写成形式进行相等性测试，其中矩阵T可以从敌手所进行的通用群操作的查询中推导出来。我们可以不进行这些查询，而是运行一个修改过的敌手，它选择另一个公共参考字符串并通过测试是否等于 0来回答查询。由于无泄漏CRS，用这种方法得到的答案极有可能与敌手在真正的公共引用字符串上看到的答案相同，因此从现在开始我们假设通用群敌手不会对包含CRS的元素进行任何零相等性测试。

        一个敌手不会对CRS进行零相等性测试，而只使用通用群操作，相当于敌手选取的矩阵与无关，之后计算出和。对等式取离散对数，这正好准确对应于一个分裂NILP知识可靠性敌手得到矩阵和证明

       对验证等式取离散对数，我们发现如果敌手成功地找到语句和有效证明，则对应求找到了语句和矩阵使得对测试矩阵有

        但是，根据分裂NILP的统计知识可靠性的定义，上述事件发生的概率可忽略的。除非敌手能够根据计算出证据，使得

        如果我们使用一个分裂NILP，它只对分裂的仿射敌手具有可靠性，这些敌手被限制输出一个矩阵，那么引理1的证明同样成立。但是，我们稍后构建的分裂的NILP实际上对任何矩阵都是安全的。这样做的好处是对密码分析进行了对冲，即使对手在G1和G2之间找到了一个有效的可计算同构，即使它将g映射到h，我们在通用群模型中仍具有安全性。另一个优点是这种结构也适用于变化很小的对称双线性群。

---

3.构造非交互式论证

        我们将构造一个仅包含3个群元素的QAP基于配对的NIZK论证。我们分两步构造，首先构造一个二次算术程序的NILP，然后观察它是一个分裂NILP，最后使用前面介绍的编译技术将它编译成基于配对的NIZK论证。

3.1 二次算术程序的非交互线性证明

         在正式证明这是一个NILP之前，我们给出一点不同的组件背后的直觉。α和β的作用是保证A,B和C在选择上的一致性。验证等式中的乘积α·β保证了A和B包含非平凡α和β组分，也就是说乘积A·B与α·β有线性关系，我们之后将证明这种线性关系只能被C与一致选择的抵消。γ和δ的作用是通过被γ和δ各自整除来让验证方程中的后两个乘积是独立于第一个乘积。γ和δ阻止了验证方程中用于不同乘积元素的混合和匹配。最后，我们使用r和s将证明随机化，得到零知识。

定理1：上述构造产生具有完美完备性，完美零知识以及抵抗仿射证明者策略的统计知识可靠性的NILP。

证明：完美完备性是很容易验证的。完美零知识来自具有均匀随机域中A,B的真实证明和模拟证明。这些元素通过验证方程唯一确定了C，因此真实证明和模拟证明具有相同的概率分布（类似sigma协议的零知识模拟那样）。

        剩下的就是 证明对于任何具有不可忽略的成功概率的仿射证明者策略，则存在一个提取器可以计算出witness。首先按照形式定义敌手A(也就是仿射证明者策略）会给提取器一个矩阵，我们设这个矩阵的第一行乘以会获得如下形式的A

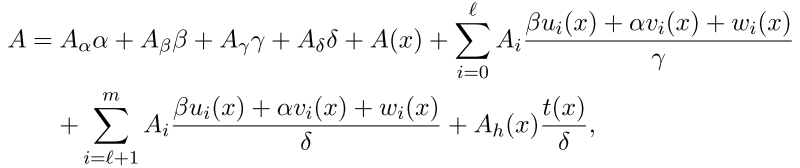
同时矩阵的第二行和第三行乘以 获得上述相同形式的B和C。

        之后, 我们将验证等式看做是关于的多元Laurent多项式(也就是多项式指数允许是负数）。这是因为Schwartz-Zipplel 引理，比如f(r)=g(r)且r是F中的随机数，那么则f(x)等于g(x)的概率至少是1-deg(f(x))/|F|。同理将验证等式从值相等转化为方程式相等也有压倒性的概率。因此验证等式可以看做是 关于的多元Laurent多项式。接下来利用验证等式两边关于的系数是相等的来消去A,B,C的系数。我仅解释前面一部分消去，后面消去系数的方式是一样的，最终会计算出witness是。

2个域元素NILPs. 

         我们很自然地会问，证明者在NILP中发送的域元素是否可以进一步减少。[DFGK14]的平方span程序给出了boolean-SAT的2个域元素的NILP。由于每个乘法门a·b = c都可以被重写为，因此也可以通过将电路重写为只使用平方门来得到算术电路可满足性的2个域元素NILP。通过在NILP中选择r = s，我们现在有了，所以证明者只需要发送两个元素A和C就可以做出a convincing proof。重写算术电路以只使用平方门可能会使门的数量增加一倍，并且还需要一些额外的导线来进行平方的减法，因此，尽管减少了NILP的大小，但会带来显著的计算成本。

 3.2 二次算术程序的NIZK论证

        现在将给出一个二次算术程序的基于配对的NIZK论证。

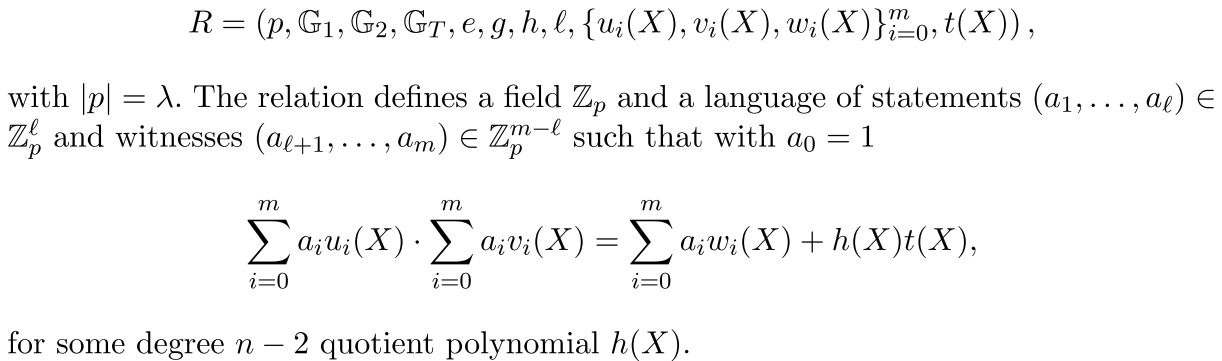
        上面给出的NILP的一个重要设计特征是很容易使其成为一个分裂的NILP。证明元素A、B和C在验证方程中只使用一次，因此很容易将它们分配到不同的双线性测试（the bilinear test）的不同边。通过将公共参考字符串分割成两部分，从而可以对证明的每一边进行计算，最终我们得到一个分裂的NILP。由此产生的拆分NILP也是不需要公开的，因此可以编译成通用群模型中的NIZK论证，正如我们在第2.5节中所做的那样。由于配对友好的椭圆曲线在G1中的群元素表示通常比G2中的要小[GPS08]，为了最大的效率，我们选择将A和C分配给第一个群，将B分配给第二个群。这给了我们下面的NIZK论证。

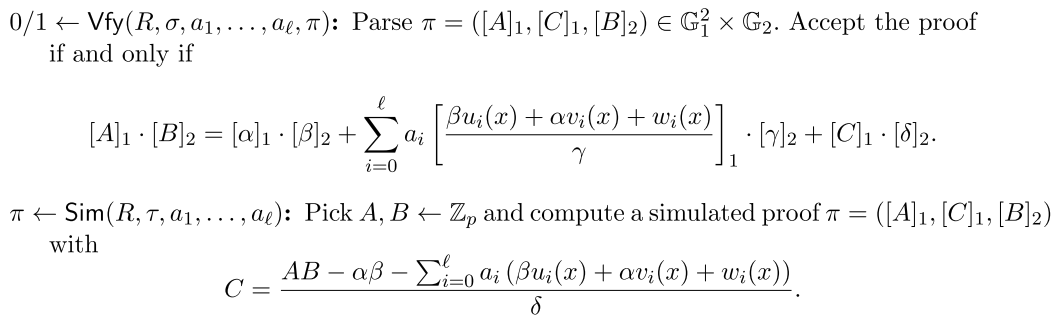
定理2.  上述协议具有完美完备性和完美零知识。对于多项式通用双线性群的敌手来说，该协议具有统计知识可靠性。

证明： 很容易看到非交互式论证编码一个分裂的NILP。如果要应用引理1，则需要证明CRS是无泄漏的。

对称双线性群

        非交互论证系统也适用于对称双线性群，其中G1 = G2, g = h，在这种情况下，公共参考串包含了[σ1]1和[σ2]2中元素的并，证明和验证方程按上述方法计算。

效率

        证明中包含G1中2个元素，G2中1个元素。CRS包含关系R、Zp中的n个元素、G1中的m+ 2n + 3个元素(也就是）、G2中的n + 3个元素（也就是）。验证者不需要完整的CRS, 只要充分知道

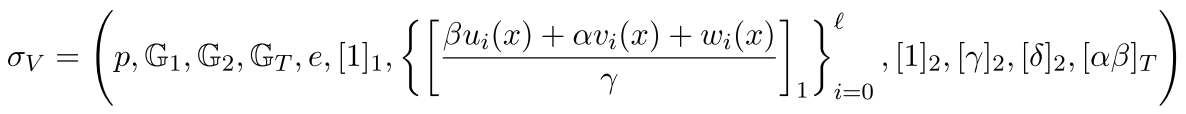
验证者的参考字符串只需包含 G1中的l+2个元素，G2中的3个元素，GT中的1个元素。 验证包括检查证明由三个适当的群元素组成，并检查单个配对运算方程。验证者计算G1中的l指数，一些群乘法运算以及三个配对运算（假设预计算在验证者的参考字符串中）。

证明者必须计算出h(X)以便用来产生证明中的C。h(x)满足下列这个等式。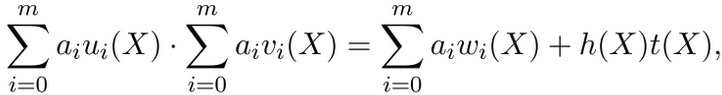

证明者可以通过计算下述n个,

然后通过拉格朗日插值来求出。如果是某个合适大小素数p的单位根，这可以使用标准的FFT技术以来计算出在n个点上值。同时也可以将FFT技术应用在拉格朗日插值法以来求出三个多项式的系数。有所有的系数之后，证明者需要在G1上做m+3n-l+3个指数运算以及在G2上做n+1个指数运算。

        渐近地，随着安全参数的增加，幂次是主要代价。然而，在实践中，对于中等的安全参数和大的语句，进入FFT计算的乘法运算可能代价更高。在这种情况下，可能需要使用一个更大的公共参考字符串，其中包含预先计算好的元素，，这样就可以直接构造A和B，而不需要证明者计算和的系数。在布尔电路的情况下，我们有，证明者可以利用这些预先计算的元素，在计算A和B时，对每个元素做m组乘法。因此，我们在表1中延长了CRS，以使证明者的计算成本较低。