Sumcheck协议学习

 参考资料: Justin Thaler《Proof, Arguments and Zero-Knowledge》

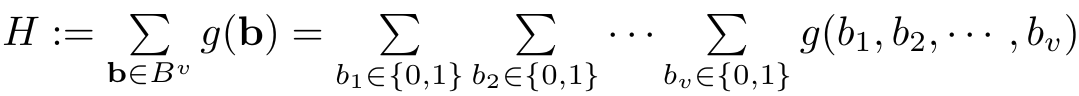
其中函数g是定义在有限域F上的v元多项式，B是有限域F的子集，但是大部分应用只会要求B={0,1}。求和验证Sumcheck协议对描述了这样一种计算模型：

        证明者Prover想要向验证者Verifier证明函数g在所有的二元输入b1,b2,....bv点上的求和值是H。如果证明者直接将b1,b2,....bv发送给验证者，则验证者需要次函数g在v个点上的计算时间。这是一个指数验证时间，对于计算资源匮乏的验证者是无法接受这一验证时间。Sumcheck协议将验证时间减少到O(v+函数g在上计算单点函数值的时间）。 

Sumcheck协议：

1.协议

假设和具有如下定义的形式：

其中,是变量，是取值，是上的随机数。上述存在等式：

证明过程如下：

        证明者Prover在最开始时发送一个值C给验证者Verifier，并声称C等于H，记作，之后，开始进行v轮的交互。是正确计算的函数，是证明者Prover宣称等于的函数。如果站在验证者一方的视角来看整个证明过程，我们并不知道证明者是如何得到一系列一元多项式的，证明者有可能通过其他方式来生成一元多项式，因此并没有在证明者Prover一方直接写。

2. 整个交互过程证明的逻辑：

         最开始，验证者Verifier验证 。 如果通过验证，则通过Schwartz–Zippel引理以压倒性的概率表明等于。

        如果等于，那么根据等式1有

如果验证者Verifier成功验证，那么有

最终，通过Schwartz–Zippel引理以压倒性的概率推导出

之后，继续按照上述过程就能成功证明C等于值H。下图是当v=3时的证明过程例子

2.正确性和可靠性分析

3.性能分析

通信开销：

        表示多项式g在第i个变量的次数。证明者每轮给验证者发送+1个元素，也就是单变量多项式的系数，因此证明者总共发送个域F上的元素。验证者每轮给证明者发送1个域F上的随机元素，因此总共发送了v个元素，因此其通信开销是。

验证时间：

       假设单变量多项式的计算时间主要取决于其项数，也就是多项式的次数+1。

       验证者每轮都要计算单变量多项式 在随机点的值，以及最后一轮需要计算多项式函数g在v个点的值，因此验证时间为。

证明时间：

        证明者每次都要计算出单变量多项式。如果将X_i也看做一个值，那么就是计算个的值，因此每轮所需的计算时间是，那么总共需要的时间是。如果，那么总共需要的时间是。

注释：

        求和验证Sumcheck协议的一个重要特征是，验证者给证明者的消息只是域中的随机元素r，完全独立于输入多项式g。验证者只需要知道多项式g的每个变量(即）的阶的上界，以及在随机点r处求值（即）的能力，也能应用Sumcheck协议。相反，证明者确实需要知道精确的多项式g，以便在Sumcheck协议的过程中计算每条消息。 

4.应用：高效的交互式证明IP计算无向图中三角形个数

        算法通常调用矩阵乘法来生成中间值，但对乘积矩阵本身不感兴趣。例如，求简单无向图中三角形的个数。如果A是n个顶点简单无向图的邻接矩阵，算法计算(已知最快矩阵乘法在内完成)，然后计算 ，三角形个数=。

         ，而表示顶点i到顶点k路径为1的个数 乘以 顶点k到顶点j路径为1的个数，相乘就是顶点i到顶点j路径为2的个数。而表示顶点i到顶点j 路径为1的个数，从而构成由顶点i到j，以及任意一个顶点构成的三角形个数。在算图中总的三角形时，每个三角形会重复算6次(i,j),(j,i),(i,k),(k,i),(j,k),(k,j)。因此总的三角形个数是。

        矩阵在这里只是作为一个中间对象，来快速推导出最终的答案。本节利用Sumcheck协议以及多线性扩展给出上述问题的交互式证明IP。假设证明者Prover已经正确计算了矩阵，并使用通过公式计算出。最重要的是，通过IP证明者将仅通过对数通信(即，不需要发送矩阵给验证者)就能完成证明，并且除了确定A2之外，只需要做很少的额外工作。                                                                                                                                                            令  ， 其中x是顶点i的二进制编号，y是顶点j的二进制编号，分别表示矩阵A和的函数。令 分别是 的多线性扩展。因此最终有

                                       

之后，证明者和验证者之间应用Sumcheck协议来验证是否有 ，协议的最后一步，需要由验证者随机选取，并计算。验证者自己需要自行计算, 而计算可以由验证者继续与证明者采用Sumcheck协议来证明

为什么会有该等式成立？可以查看书中的引理4.2

最后，该Sumcheck协议需要验证者在最后计算和。

        总结，想要应用Sumcheck协议，就要考虑如何将问题转化为Sumcheck协议等式，尤其是构建域F上的m元多项式。 然而，一般都会先将问题转化为函数，因此需要进行多线性扩展从而构建函数。然后，找到一个求和的范围，最后才能进行Sumcheck协议。