4.AcWing 788. 逆序对的数量（AcWing算法基础课二刷）

浩子诚

已于 2023-09-30 00:32:44 修改

阅读量97

点赞数 2

分类专栏： AcWing算法基础课二刷文章标签：算法

于 2023-09-25 13:36:05 首次发布

本文链接：https://blog.csdn.net/qq_37850601/article/details/133270644

版权

AcWing算法基础课二刷专栏收录该内容

8 篇文章 0 订阅

订阅专栏

关键词：归并排序、逆序对
原题链接：活动 - AcWing
这道题不像快速排序的课后习题一样，需要你自己思考，但懂得原理之后你会发现其实很简单。
对于部分情况，归并排序求逆序对很好用。
首先我们来想暴力的方法吧。
给你一个这样的序列：2 3 4 5 6 1
我们可以清楚的看到：(2,1) (3,1) (4,1) (5,1) (6,1)是逆序对，那么这个序列的逆序对有5个，用
肉眼观察就可以得出结论。暴力的方法是：固定当前的数，往后遍历序列，找到比这个数小的
数，就增加一个逆序对的数量。
很明显，这种暴力做法的时间复杂度是 $O\left ( n^2 \right )$ 。

下面来展示 $O\left ( n^2 \right )$ 做法的代码，有两个测试点TLE（超时）：

#include<iostream>
using namespace std;
const int N=1e5+10;
int a[N];
long long ans=0;
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++) 
    scanf("%d",&a[i]);
    for(int i=1;i<=n;i++)
    {
    for(int j=i+1;j<=n;j++)
    if(a[i]>a[j]) ans++;
    }
    printf("%lld",ans);
    return 0;
}

对于有1000个元素的数组，这种做法还可以接受；但题目的数组大小最多可以达到100000，这时候就不可以用 $O\left ( n^2 \right )$ 的时间复杂度来解决这道问题。

换言之，我们必须寻找 $O\left (n \sqrt{n}\right )$ 及以下的时间复杂度的算法解决这道问题。

用什么方法可以解决？

有两种方法：Ⅰ.归并排序；Ⅱ.树状数组，在这道题的时间复杂度都是 $O\left ( nlogn \right )$ 。

在这里我们主要讲第一点方法——归并排序求逆序对。

在上一篇文章中，我们提到过归并排序的一个重要性质：当前层的归并排序中，left和right数组都是有序的，在下一层中已经排列完成。此时我们只要将当前层的逆序对找出来就可以了。每一层找逆序对的时间复杂度是 $O\left ( n \right )$ ，总共有 $logn$ 层（log以2为底），时间复杂度是 $O\left ( nlogn \right )$ 。

那么如何用归并排序寻找逆序对？

这个问题提的非常好。跟上篇文章一样，采用双指针思想解决问题。

y总的算法基础课视频中讲的非常清楚，求逆序对的过程也是“从底层向顶层”的。

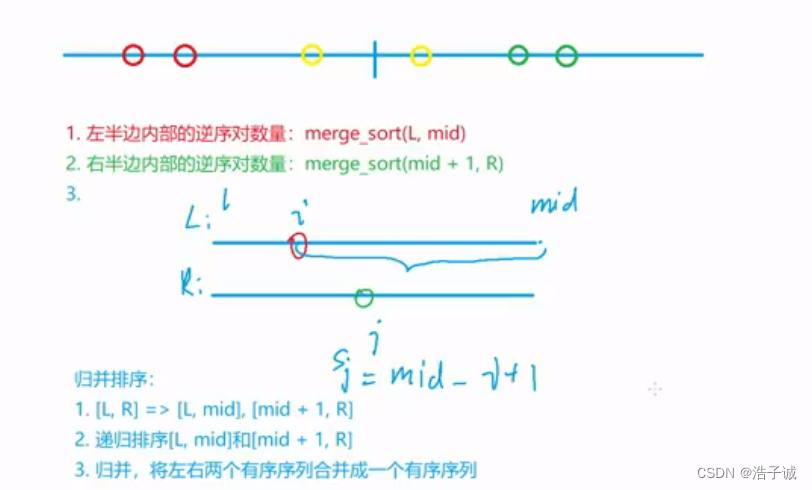
当前层的逆序对数量分为三个部分：

1.左半边的逆序对数量，在下一层已经求好（left部分已经排序过）；

2.右半边的逆序对数量，在下一层已经求好（right部分已经排序过）；

3.逆序元素一个在左半边，一个在右半边，此时用双指针计算逆序对。

我们可以在归并排序的过程中同时计算逆序对，如下图所示：

如果a[j]<a[i]，那么a[i]到a[mid]的所有数都与a[j]形成逆序对，之后a[j]进入tmp数组。

所以逆序对的公式是：

ans=mid-i+1;(表示i到mid的元素个数）

注意我们只需要计算right相对于left的逆序对，left指针移动时不需要计算。

（计算left相对于right的逆序对似乎也可行，不过我没试过哈哈）

下面将进行一个详细的模拟，还是引用上一篇文章的数组：

left：2 5 7 9 10

right： 1 3 4 6 8

1比2小，1存入tmp，逆序对+5，right指针指向3；

2比3小，2存入tmp，left指针指向5；

3比5小，3存入tmp，逆序对+4，right指针指向4；

4比5小，4存入tmp，逆序对+4，right指针指向6；

5比6小，5存入tmp，left指针指向7；

6比7小，6存入tmp，逆序对+3，right指针指向8；

7比8小，7存入tmp，left指针指向9；

8比9小，8存入tmp，逆序对+2，right数组元素全部存入tmp。

剩下的9 10也一并存入tmp中，不增加逆序对个数。

之后再把tmp数组代替left和right数组，即当前正在递归的数组。

所以当前层的逆序对个数是5+4+4+3+2=18个。

我们可以保证这种方法找出的逆序对数量不重不漏，读者可以自己打草稿模拟。

读者也可以自己构造一个数组进行验证。

注意：两个元素相等不算逆序，因此不构成逆序对。

不过要提醒一点：既然数组最多有100000个元素，那么最极端的情况是：这个序列是严格逆序的，即100000 99999 ... 3 2 1。那么逆序对的数量是1+2+...+99999。用高中数列公式 $S_{n}=\frac{n(n+1)}{2}$ 易得这种情况有99999*50000=4999950000个逆序对。而int可表示的最大范围是2147483647（即2^31-1)，所以必须开long long，以防溢出。

long long有时候会在一道算法题用到很多次，因此用两个方法可以达到简写的效果：

Ⅰ.#define ll long long （不需要加分号）

Ⅱ.typedef long long ll;（需要加分号）

都表示在接下来的代码中，你可以用ll代替long long节省时间，从而加快做题速率。

说一句题外话：忘记开long long是算法竞赛、考研上机考试中最容易犯、也是最常见的错误之一。因此青少年OI竞赛流传这样一句话：“十年OI一场空，不开long long见祖宗”。因此，在做每一个算法题之前、或想到用某个算法做题之前，都需要算出时间复杂度是否可行、需不需要开long long甚至手写高精度（对C/C++而言），这需要你的数学思维和功底。

如果在比赛时间不充裕时突然发现没有开long long，那么也可以用上述的方法替换。

这是一种万不得已的方法，可能会报错；所以尽量手动修改。

typedef int long long;

此时需要把main函数改为signed类型，否则会出错。

最后是大家喜闻乐见的上代码环节：（手动滑稽）

#include<iostream>
using namespace std;
const int N=1e5+10;
typedef long long ll;//缩写long long
int a[N],tmp[N];
//边归并排序边计算逆序对
ll mergeSort(int l,int r)//上篇文章有逆序对的详细注释
{
    if(l>=r) return 0;
    int mid=(l+r)>>1;
    int pos=0,i=l,j=mid+1;
    //上图中左边的逆序对和右边的逆序对（1、2）的情形
    ll res=mergeSort(l,mid)+mergeSort(mid+1,r);
    while(i<=mid&&j<=r)
    {
        if(a[j]<a[i]) //注意要严格小于，等于不算逆序
        {
            tmp[pos++]=a[j++];
            res+=mid-i+1;//刚才推的公式
        }
        else tmp[pos++]=a[i++];
    }
    while(i<=mid) tmp[pos++]=a[i++];
    while(j<=r)  tmp[pos++]=a[j++];
    for(int i=l,j=0;i<=r;i++,j++)
    a[i]=tmp[j];
    return res;
}
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%d",&a[i]);
    //在排序好数组的同时计算逆序对，要开long long
    ll ans=mergeSort(1,n);
    printf("%lld",ans);//long long的输出格式是%lld
    return 0;
}

感谢您的支持