【学习笔记】InformationTheory——熵，条件熵，联合熵，互信息，交叉熵

Last updated: 2019-12-21

参考：

• 本文主要内容来自于：《数学之美》第6章 信息的度量和作用
• 补充内容来源于网络，主要包括但不限于：Wikipedia: Mutual information，维基百科：互信息，CSDN：信息论：熵与互信息（皮皮的blog）

1948年，香农（Claude Shannon）在他著名的论文“通信的数学原理”（A Mathematic Theory of Communication）提出了 “信息熵” 的概念，解决了信息的度量问题，并且量化出信息的作用。

信息熵

不确定性越高，这条信息的信息量越大；不确定性越低，信息量越小。

如何量化？

猜数字游戏：主持人在纸上写下一个[1,64]之间的整数，你来猜这个数字是什么。你每猜一次，我会告诉你对或者不对。问最少需要几次可以得出正确答案？——6次：二分问法，第一次问“答案≤32吗”；若是，第二次问“答案≤16吗”…——$lo{g}_{2}64=6$，只要6次就可以问出正确答案。

用 比特（Bit） 来度量信息量，则上述中的信息量为 6 Bits。信息量的比特数和所有可能情况的对数函数 $\log$ 有关（如无特殊说明，本文一律以2为底）。

上面的游戏中认为主持人写下每个整数的概率是相等的，但是如果概率是不等的，可能不需要6次就可以猜出来了。比如如果写$[1,8]$的可能性最大，那第一次猜的时候就可以先问“是≤8吗”。

香农给出的信息量度量公式为：
$$H=-(p_1\cdot \log p_1+p_2\cdot \log p_2+\cdots +p_{64}\cdot \log p_{64})$$
当64个数字等概率时，每个 $p=1/64$，$-\log p=-\log \frac{1}{64}=6$，可以证明上面式子最大值即为6，也就是均与分布时不确定性最大，信息量也最大。

信息熵（Entropy），$H$，单位比特，定义如下：
$$H(X)=-\sum _{x\in X}P(x)\log P(x)\text{\hspace{1em}(1)}$$
变量不确定越大（均匀分布是最大），熵就越大，要把它搞清楚所需要的信息量也就越大。

补充：

• 熵的单位取决于定义用到的对数的底：底为2时，单位为bit；底为e时，单位为 nat；底为10时，单位为Hart。
• 熵的取值范围为 $[0,\log |X|]$ ($|X|$表示$X$的取值个数)
• 具有均匀概率分布的信源符号集可以有效地达到最大熵：所有可能的事件是等概率的时候，不确定性最大。

🍉一本50万字的中文书《史记》平均有多少信息量呢？

• 已知常用的汉字（一级二级国标）大约有7000字。如果每个字等概率，则大约需要13比特（$2^{13}=8192$）表示一个汉字。用两字节的国标编码存储这本书大约需要 1MB。
• 但汉字使用频率是不均等的，前10%的汉字占常用文本的95%以上，若只考虑每个汉字的独立概率，每个汉字的信息熵大约只有8~9比特；再考虑上下文的相关性，则只有5比特左右。所以压缩之后存储这本书大约只要 320KB。
• 这两个数量的差距称为**“冗余度”（Redundancy）**。不同语言冗余度差别很大，汉语在所有语言中冗余度相对较小，是最简洁的语言。

信息的作用

一个事物内部会有随机性，也就是不确定性，假定为 $U$，而从外部消除这个不确定性唯一的办法是引入信息 $I$，而需要引入的信息量取决于这个不确定性的大小，即要 $I>U$ 才能完全消除。当 $I<U$ 时只能消除一部分不确定性。

几乎所有的自然语言处理、信息与信号处理的应用都是一个消除不确定的过程。

自然语言的统计模型中，一元模型是通过词本身的概率分布来消除不确定因素，而二元及更高阶的语言模型还使用了上下文的信息。

在数学上可以严格证明为什么这些“相关的”信息也能消除不确定性——条件熵（Conditional Entropy）。

条件熵（Conditional Entropy）

假设 $X$ 和 $Y$ 是两个随机变量，$X$ 是我们想要了解的。假定现在已经知道了 $X$ 的随机分布 $P(X)$，$X$ 和 $Y$ 一起出现的联合概率分布（Joint Probability），在 $Y$ 取不同值的前提下 $X$ 的条件概率分布（Conditional Probability）。定义在 $Y$ 的条件下的条件熵为：
$$H(X|Y)=-\sum _{x\in X,y\in Y}P(x,y)\log P(x|y)\text{\hspace{1em}(2)}$$
可以证明 $H(X)\ge H(X|Y)$，也就是说多了 $Y$ 的信息之后，关于 $X$ 的不确定性降低了！

在统计语言模型中，如果把 $Y$ 看成是前一个字，那么数学上就证明了二元模型的不确定性小于一元模型。

同理可以定义有两个条件的条件熵：
$$H(X|Y,Z)=\sum _{x\in X,y\in Y}P(x,y,x)\log P(x|y,z)$$
可以证明 $H(X|Y)\ge H(X|Y,Z)$ ，也就是说三元模型比二元模型好。

🍉一个有意思的问题：上述式子中等号什么时候成立？

• 等号成立说明增加了信息，不确定性却没有降低。
• 如果获取的信息与要研究的事物毫无关系，则等号就成立。

那么如何量化这种相关性呢？👇

互信息（Mutual Information）

——两个随机事件“相关性”的量化度量。

假定有两个随机事件 $X$ 和 $Y$ ，它们的互信息定义如下：
$$I(X;Y)=\sum _{x\in X,y\in Y}P(x,y)\log \frac{P(x,y)}{P(x)P(y)}\text{\hspace{1em}(3)}$$
可以证明：互信息 = $X$本身的不确定性 - 在知道 $Y$ 的条件下 $X$ 的不确定性
$$I(X;Y)=H(X)-H(X|Y)\text{\hspace{1em}(4)}$$
所以所谓的两个事件相关性的量化度量，就是在了解了其中一个$Y$的前提下，对消除另一个$X$不确定性所提供的信息量。（知道$Y$时，对$X$不确定度减少的程度）

【说明一下】

1. $I(X;Y)$的取值范围为 [ 0 , min ⁡ { H ( X ) , H ( Y ) } ] [0, \min\{H(X), H(Y)\}] [0,min{H(X),H(Y)}] ，
   • 用琴生不等式可以证明$I(X;Y)\ge 0$，从而也就证明了$H(X)\ge H(X|Y)$
2. 当$X$和$Y$完全相关时，$P(x,y)=P(x)=P(y)$，取值为1；
3. 当两者完全无关时，$P(x,y)=P(x)P(y)$，取值为0。

补充：

• 互信息是 X 和 Y 的联合分布相对于假定 X 和 Y 独立情况下的联合分布之间的内在依赖性。
• （所以 log 里，分子$P(x,y)$是 X 和 Y 的实际的联合分布，分母$P(x)P(y)$是假定两者独立时的联合分布）
• 互信息越小，两个来自不同事件空间的随机变量彼此之间的关系性越低; 互信息越高，关系性则越高 。

在自然语言处理中，只要有足够的语料，就很容易估计出互信息公式中的$P(X,Y)$，$P(X)$，$P(Y)$三个概率，从而很容易计算出互信息。因此互信息被广泛用于度量一些语言现象的相关性。

机器翻译中最难的两个问题之一就是词义的二义性（又称歧义性，Ambiguation）问题。使用互信息是解决这个问题最简单而实用的方法。例如：

• Bush 一词可以是美国总统的名字，也可以是灌木丛。
• 解决思路：首先从大量文本中找出和总统Bush一起出现的互信息最大的一些词，比如总统、美国、国会、华盛顿等等；然后用同样的方法找出和灌木丛一起出现的互信息最大的词，如土壤、植物、野生等等。有了这两组词，在翻译Bush时，看看上下文中哪类相关的词多就可以了。

相对熵/交叉熵（Relative Entropy，或Kullback-LeiblerDivergence）

——信息论中另一个重要的概念

用来衡量两个取值为正数的函数的相似性，定义如下：
$$KL(f(x)||g(x))=\sum _{x\in X}f(x)\cdot \log \frac{f(x)}{g(x)}\text{\hspace{1em}(5)}$$
三个结论：

1. 对于两个完全相等的函数，它们的相对熵=0；
2. 相对熵越大，两个函数差异越大；反之，相对熵越小，两个函数差异越小；
3. 对于概率分布或者概率密度函数，如果取值大于等于0，相对熵可以度量两个随机分布的差异性。

相对熵是不对称的：
$$KL(f(x)||g(x))\ne KL(g(x)||f(x))$$
为了让它对称，提出一种新的相对熵的计算方法，将上面不等式两边取平均：
$$JS(f(x)||g(x))=\frac{1}{2}[KL(f(x)||g(x))+KL(g(x)||f(x))]\text{\hspace{1em}(6)}$$

应用：

• 信号处理：如果两个随机信号，相对熵越小，说明两个信号越接近；反之两个信号差异越大。
• 信息处理：衡量两段信息的相似程度，比如论文查重，如果一篇文章照抄或者改写另一篇，那么这两篇文章中次品分布的相对熵就非常小，接近于0。
• Google的自动问答系统：衡量两个答案的相似性。
• 自然语言处理：衡量两个常用词（在语法和语义上）在不同文本中的概率分布，看它们是否同义。
• 信息检索：一个重要概念：词频率-逆向文档频率（TF-IDF）

小结

熵、条件熵、相对熵——这三个概念与语言模型的关系非常密切。

如何定量地衡量一个语言模型的好坏？

• 一个很自然的想法：错误率。例如语义识别或机器翻译的错误率。——但是这种测试方法对于语言模型的研究人员来讲，既不直接也不方便，而且很难从错误率反过来定量度量语言模型。
• 语言模型是为了用上下文预测当前的文字，模型越好，预测得越准，那么当前文字的不确定性就越小。——而信息熵正是对不确定性的衡量。
  • 贾里尼克提出**语言模型复杂度（Perplexity）**的概念
  • 物理意义：在给定上下文的条件下，句子中每个位置平均可以选择的单词数量。
  • 一个模型复杂度越小，每个位置的词就越确定，模型越好。

困惑度(perplexity)：它主要是根据每个词来估计一句话出现的概率，并用句子长度作normalize，公式为：
$$\begin{gathered} PP(S)=P(w_1{w}_2...w_N{)}^{\frac{1}{N}} \\ =\sqrt[N]{\frac{1}{p(w_1{w}_2...w_N)}} \\ =\sqrt[N]{\prod _{i=1}^N\frac{1}{p(w_i|w_1{w}_2...w_{i-1})}} \end{gathered}$$
或者等价地，
$$PP(s)=2^{-\frac{1}{N}\sum \log (P(w_i))}$$

补充

---

（参考来源：CSDN：皮皮blog）

联合熵(Joint Entropy)

条件熵(conditional entropy)

联合熵 和 条件熵 的关系

连锁规则。描述 x 和 y 所需的信息是描述 x 自己所需的信息，加上给定 x 的情况下具体化 y 所需的额外信息。

---

互信息：

互信息又可以等价地表示成：

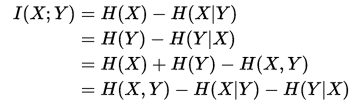
用Venn图表示：

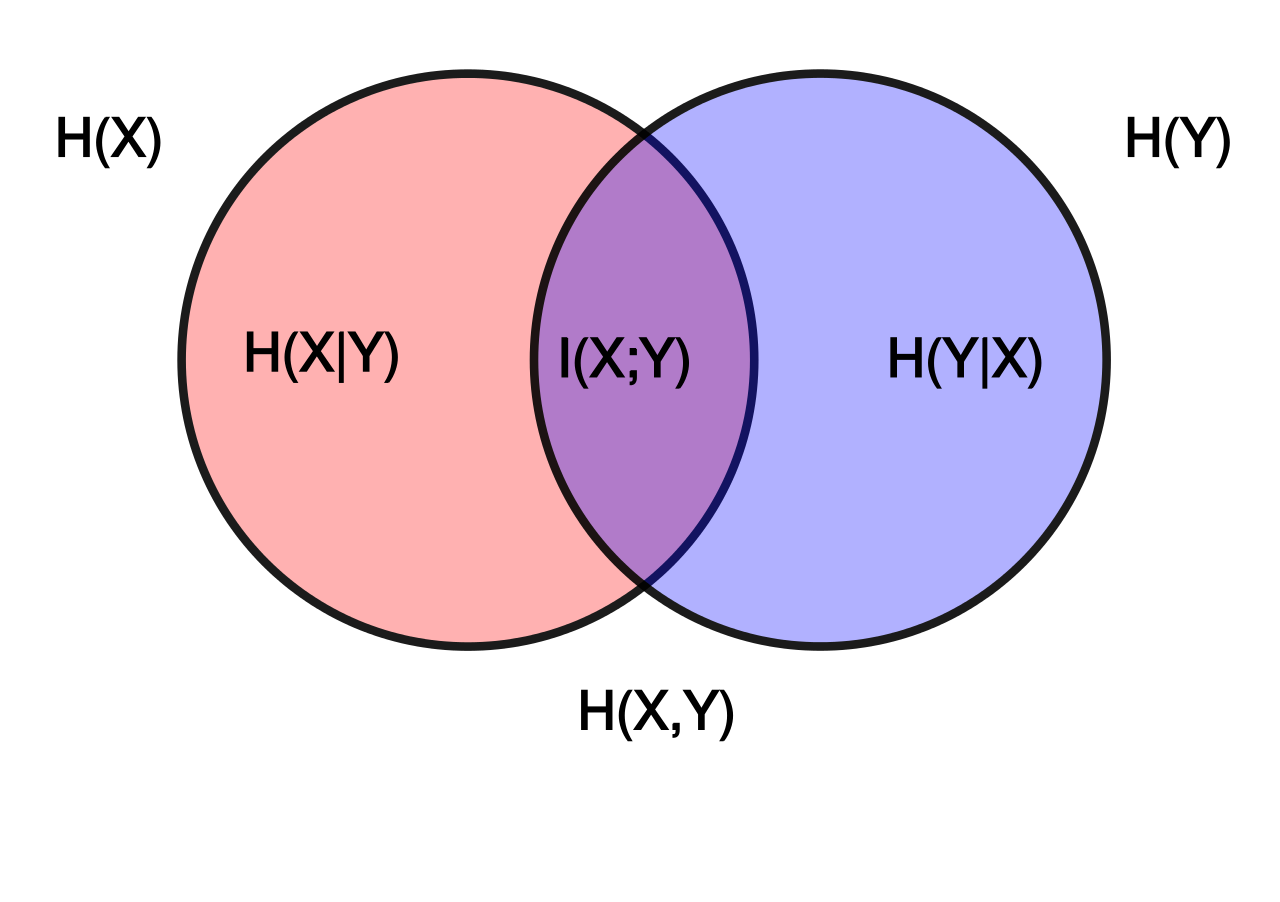
(图片来源：维基百科)

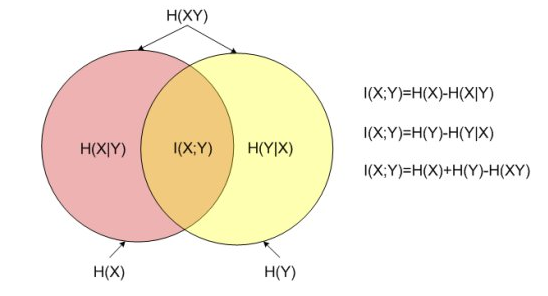
(图片来源：CSDN：皮皮blog)

互信息的推导：

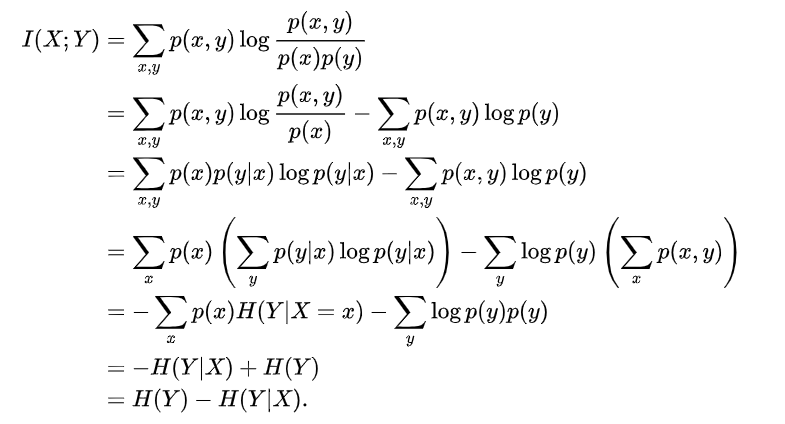
--------完--------