机器学习之PCA降维

目标：尽量减少重建错误，最小化原始点与其投影之间的欧几里德距离

另一个目标：最大化方差，为了识别我们想要研究观察变异的模式
PCA解决方案解决了这个问题！
PCA - 通过具有单一自由度的2D数据重建2D数据。 通过欧几里德距离评估重建

Principal Component Analysis (PCA)：

PCA：将一组可能相关变量的观测值转换为一组称为主成分的线性不相关变量值
该变换以这样的方式定义：第一主成分具有尽可能大的方差，并且每个后续成分在与前面的成分正交（即不相关）的约束下具有可能的最高方差。

如何确定方差最大的方向？
假设X包含n个数据点，并且每个数据点都是p维的，即

现在，我们想找到这样一个单位向量?1，

 covariance matrix 是协方差矩阵

由于α是单位向量，α^?α= 1，基于拉格朗日乘数法，我们需要，

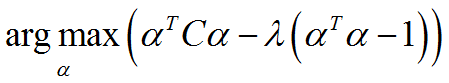
对上式求导：

因此，α1应该是对应于C的最大特征值的特征向量。

什么是与α1正交的另一个方向α2，并且数据可以具有第二大的变化？
答：它是与C的第二大特征值λ2相关的特征向量，这种方差是λ2

结果：C的特征向量形成一组正交基，它们被称为原始数据X的主成分
您可以将PCs视为一组正交坐标， 在这样的坐标系下，变量互不相关。

在PC中表达数据
假设{α1，α2，...，α?}是从X派生的PC，?∈ℝ^（?×1）
然后，数据点X?∈ℝ^（?×1）可以由{α1，α2，...，α?}线性表示，并且表示系数是

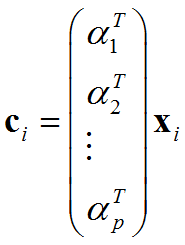
实际上，c?是{α1，α2，...，α?}所在的新坐标系中X?的坐标。

总结：
?是一个数据矩阵，每列都是一个数据样本
假设它的每个特征都是零均值

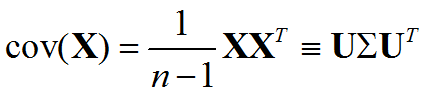
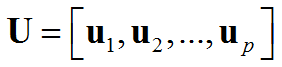拓展了一个新的空间，新空间中的数据表示为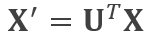

在新的空间中，数据的维度不相关。

协方差矩阵：

分别为m 与n 个标量元素的列向量随机变量X 与Y，二者对应的期望值分别为μ与ν，这两个变量之间的协方差定义为m×n 矩阵

两个向量变量的协方差cov(X, Y)与cov(Y, X)互为转置矩阵。

协方差有时也称为是两个随机变量之间“线性独立性”的度量，但是这个含义与线性代数中严格的线性独立性线性独立不同。

举例：

新坐标系中数据点的坐标：

新坐标系中数据点的坐标，在图上绘制newC，在这样一个新系统中，两个变量是线性无关的！

使用PCA减少数据维数：

假设是主成分

如果全部被使用，则仍然是p维的

如果只有m个被使用，则??将是m维的

也就是说，数据的维度减少了！

 

新坐标系中数据点的坐标：

如果仅保留第一主成分（对应于最大特征值）

Metric learning：指标学习

每个样本空间定义属性的距离度量
我们的目标是找到一个样本空间，样本可以在适当的距离测量方法下正确分组

Distance measures：距离测量

距离度量的一些性质????（⋅，⋅）：
非负：????（??，??）≥0
身份：????（??，??）= 0 当且仅当 ??=??
对称：????（??，??）=????（?j，??）
三角不等式：????（??，??）≤????（??，??）+????（??，??）
闵可夫斯基距离：

Extension of Euclidean distance：欧氏距离的延伸
样本??和??之间的欧几里德距离包含d个特征：

如果每个特征的重要性不同，我们会引入特征的权重：

马哈拉诺比斯距离：Mahalanobis distance

W ---> M, M是对称的半正矩阵
我们可以有马哈拉诺比斯距离:

M称为度量。马哈拉诺比斯距离是点P与分布 ? 之间距离的度量。我们希望学习一个与某些数据分布相对应的度量M.

Learn a metric using priori knowledge:使用先验知识学习指标

如果已经给出了一些先验知识
必须链接集ℳ：如果（?_?，?_?）∈ℳ，表示?_?和?_?相似
不能链接集?：如果（?_?，?_?）∈?，表示?_?和?_?不相似
我们可以通过解决以下优化问题找到度量M.

Dimension reduction using a learned metric：使用学习指标降低维数

如果学习度量?是低秩矩阵，我们可以通过执行特征值分解找到一组正交基。
矩阵?∈ℝ^（?×????（?））可用于减小样本空间的维数

 

【内容来自上课的PPT】