hihocoder 1083 积分，计算几何

hihocoder 1083

描述

在平面上有一个顶点数为N的多边形P，区域

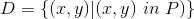
你需要写一个程序计算这个积分

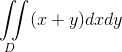
输入

输入包含T (T<=500)个测试用例。数字T在输入文件的第一行给出。每个测试用例的第一行是一个整数N代表多边形的点数。其后跟随N行，每行包含两个点Xi和Yi，表示第i个点的坐标，当我们以给定的顺序连接这些点，我们得到了一个多边形。题目保证多边形不自交，这个多边形的面积也不会是零，也不会出现3个相邻的点共线的情况。

【参数说明】

3 <= N <= 8000

|Xi|, |Yi| <= 20000

输出

对于每个测试用例行输出结果占一行。将答案四舍五入到小数点后两位（0.005四舍五入到0.01）。

解题

这个题目主要的点在于这个重积分式子可以变形。

重心公式=$x_g=\frac{\iint_{D} x dxdy}{\iint_{D} dxdy},y_g=\frac{\iint_{D} y dxdy}{\iint_{D} dxdy}$

so，这里：

$\iint_{D}(x+y) dxdy=\iint_{D} x dxdy +\iint_{D} y dxdy=(x_g+y_g)s$ ，s自然是这个多边形的面积。

求解三角形重心：$(x_{p_0}+x_{p_1}+x_{p_2})/3=x_g$

​ ​ ​ ​ ​ ​ ​ ​ $(y_{p_0}+y_{p_1}+y_{p_2})/3=y_g$

要求的就变成了重心，求多边形的重心不好处理，但是我们分割多边形成多个三角形，因为这个多边形是可以为凹多边形，所以应该用叉积求面积，这样的面积有方向性， 可以抵消凹多边形带来的问题，最后要判断这个这个多边形面积总和的方向性，因为如果最后的面积是负数，说明我们得到的答案是最终答案的负数。就要取反。

代码

#include <bits/stdc++.h>
using namespace std;
struct Point{
    double x,y;
    Point(double x,double y):x(x),y(y){}
    Point(){}
};
typedef Point Vector;
Point operator+(Point a,Point b){return Point(a.x+b.x,a.y+b.y);}
Point operator-(Point a,Point b){return Point(a.x-b.x,a.y-b.y);}
Point operator*(Point a,double D){return Point(a.x*D,a.y*D);}
Point operator/(Point a,double D){return Point(a.x/D,a.y/D);}
bool operator < (const Point &a, const Point & b){return a.x < b.x || (a.x == b.x && a.y < b.y);}
const double eps=1e-10;
int dcmp(double x){if(fabs(x)<eps) return 0; else return x<0?-1:1;}
bool operator==(const Point& a,const Point& b){return dcmp(a.x-b.x)==0&&dcmp(a.y-b.y)==0;}
/*
 dot        向量间的点积
 length     向量的模
 angle      向量间的夹角弧度
 cross      向量间的叉积
 area2      三点围成三角形有向面积的两倍
 rotate     向量绕起点逆时针旋转一定弧度后的向量
 normal     求向量的单位法线
 torad      角度化弧度
*/
double dot(Vector a,Vector b){return a.x*b.x+a.y*b.y;}
double length(Vector a){return sqrt(dot(a,a));}
double angle(Vector a,Vector b){return acos( dot(a,b)/length(a)/length(b) );}
double angle(Vector a){return atan2(a.y,a.x);}
double cross(Vector a,Vector b){return a.x*b.y-a.y*b.x;}
double area2(Point A,Point B,Point C){return cross(B-A,C-A);}
Vector rotate(Vector a,double rad){
  return Vector(a.x*cos(rad)-a.y*sin(rad),a.x*sin(rad)+a.y*cos(rad));
}
Vector normal(Vector a){double l=length(a);return Vector(-a.y/l,a.x/l);}
double torad(double deg){
    return deg/180 * M_PI;
}
int convexHull(Point *p,int n,Point* ch) {
  sort(p,p+n);
  int m=0;
  for(int i=0;i<n;i++){
    while(m>1&&dcmp(cross(ch[m-1]-ch[m-2],p[i]-ch[m-2] ))<=0 )m--;
    ch[m++]=p[i];
  }
  int k=m;
  for(int i=n-2;i>=0;i--) {
    while(m>k&&dcmp(cross(ch[m-1]-ch[m-2],p[i]-ch[m-2]))<=0)m--;
    ch[m++]=p[i];
  }
  if(n>1)m--;
  return m;
}
const int maxn = 8000+10;
Point po[maxn];

double countfun(Point p0,Point p1,Point p2)
{
    double s = area2(p0,p1,p2)/2;
    double xg = (p1.x + p0.x + p2.x) / 3.0;
    double yg = (p1.y + p0.y + p2.y) / 3.0;
    return (xg+yg)*s;

}
int main()
{
    freopen("in.txt","r",stdin);
    int T;
    scanf("%d",&T);
    while(T--) {
        int x,y,n;
        scanf("%d",&n);
        for(int _=0;_<n;_++ )
            scanf("%lf%lf",&po[_].x,&po[_].y);
        double ans = 0;
        double s = 0;
        for(int i=1;i<n-1;i++) {
            ans+=countfun(po[0],po[i],po[i+1]);
            s+=area2(po[0],po[i],po[i+1])/2;
        }
        if(s<0) ans=-ans;
        cout << fixed << setprecision(2) << ans << endl;
    }
    return 0;
}