电路分析——向量法

复数

共四种形式，结合欧拉公式变换，其实就三种形式。他们分别是：



结合欧拉公式，其实就是四种了，欧拉公式：
可得：

欧拉公式的证明：

幅值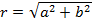：相角：

复数的运算

复数相加（或相减）就是直接将它们的实部和虚部分别相加（或相减）进行：


在图形上，这个过程等同于两个矢量相加（或相减）的平行四边形定律（phasor）两个复数相乘可以将一个复数的每个部分乘以第二个复数的各个部分，然后将四个乘积相加，得到最终的值。

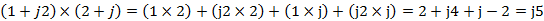
在图形上，这个过程与矢量的内积并不相同，如果将每个复数看成复平面（实轴与虚轴组成）上的矢量，其相乘结果仍为一个复数，也就是说两个复数相乘结果为复平面上的一个矢量（复数），而矢量的内积则为一个实数。

不管是点乘还是叉乘，与两个复数相乘都不同
关于两个复数相乘还可以从其指数形式考虑，也就是著名的棣莫佛定理（De Moivre’s formula）：
棣莫夫定理也是我们利用相量法计算的一个重要依据，复指数形式相乘表现为幅值相乘，相角相加。我们如果用极坐标式来表示，也就是模相乘，角相加。

相量法

相量法的基础在于这个关系式：

由这个式子可以得到：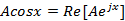
其中Re[]是取实部的意思，对于正弦时变函数

可得：

其中，
称为对应于该正弦时变函数的相量，这是一个复数。也就是说对应于一个正弦时变函数的相量是一个复数，其模大小与余弦函数的幅度相同，其相位角等于 时刻余弦函数的相位。
相量引入的意义值得思考，相量作为一个复数引入正交时变函数直观上看将余弦函数的初相与其幅值合并，一定程度简化计算。
其简化计算的根本原因，还是欧拉公式与棣莫弗定律，由此二者得来四种复数表示形式，从而把复杂的运算转变成了简单的计算。
举一个例子，分析两个正弦时变函数（具有相同频率的）的加法: