马尔科夫随机场做图像分割

引言

本文尽量避免了算法本身的一些复杂公式，结合自己的理解展示了如何实现马尔科夫随机场并将其应用到图像分割问题上，只要懂贝叶斯公式，懂得正态分布，就可以看懂本文的原理介绍。

首先用一句话概括：根据观测到的图像（各点像素值X），我们要求得对应像素的类别（Y），即求最大后验概率P（Y|X）

有些伙伴可能会有些疑惑，只知道像素值为什么可以求类别呢？瞎猜吗？当然不是，这里面包含了很严谨的数学原理，就是应用概率进行推测，下面将慢慢给大家介绍。

初始条件

1.观测一副图像，可以知道图像的特征图（Xij表示对应像素的灰度值），这里仅考虑3x3的图像，实际应用中，估计每个点的类别时，也只需要考虑8领域像素即可，这里应用到了马尔科夫的特性，总结起来就是每个点的属性仅与和他有边连接的点有关（局部马尔科夫性，全局马尔科夫性，成对马尔科夫性等，详情可自行搜索了解），在图像中，就是这个点的8领域，其中xij表示对应点的像素值，本文以灰度图为例。

2.初始化各像素点的类别，可以随机瞎猜，也可以是k-means甚至是语义分割后的结果，以下图为例，随机初始化。

3.理解一下几个概率的概念：

先验概率P（Y）：根据经验，或者是已有的观测数据中得到的，在图像分割问题中，可以是8领域像素中各类出现的频率

举个例子：P(Y=1)=2/8，中间像素的8领域中有两个属于类别1，根据这个知识，猜测中间像素是类别1的概率为2/8，这就是先验概率，同理可以求得P(Y=2)=4/8， P(Y=3)=2/8。

后验概率P(Y|X）：观测到图像的像素特征X，那么这个像素属于Y类的概率，也是本文要求的最终目标。

类条件概率P(X|Y)：如果我已经知道像素的类别了，他的像素值是多少的概率。需要假设类条件概率服从正态分布（如果要问我为什么的话，还请大佬留言互相讨论一下）

即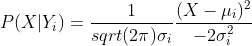，下标i表示不同的类别，公式中的均值和方差表示类别i的像素的均值和方差

4.根据贝叶斯公式：P(Y|X）*P(X）=P(X|Y）*P(Y）,由于X是观测到的图像特征，P(X)是一个常数，所以

P(Y|X）与P(X|Y）*P(Y）成正比，P(X|Y）可以根据正态分布求得，P(Y)可以根据邻域先验知识求得，所以P(Y|X）也可求

估计像素的最大后验概率P(Y|X）

分割前，分类数需要给定，本文假设3分类

1）根据上面给出的例子，分别求出了属于各类别的先验概率：P(Y=1)=2/8，P(Y=2)=4/8， P(Y=3)=2/8

2）求各类别像素值的均值和方差，根据正态分布求P(X|Y)：

类别1的均值u1=(X12+X33)/2，方差代公式求就好

同理类别2的均值u2=(X11+X13+X21+X23)/4

类别3的均值u3=（X31+X32）/2

将X=X22（待求目标像素值），以及求出的各类别像素的均值和方差代入正态分布公式中，即可求得P(X|Y1),P(X|Y2),P(X|Y3)

3）根据贝叶斯公式可求P(Yi|X）=kP(X|Yi）*P(Yi），k是一个常数，与类别和像素值都无关，所以P(X|Yi）*P(Yi）最大的类别，即为待求像素最有可能的所属类别

试验测试

女神lena

随机初始化类别，本文预设分类数为6，可以看出来刚开始完全是瞎猜的，接下来就给大家演示一下数学的奥妙，我猜着猜着就能猜出个大概了

迭代一步后

两步

5步