Matlab蚁群算法和时间序列

蚁群算法

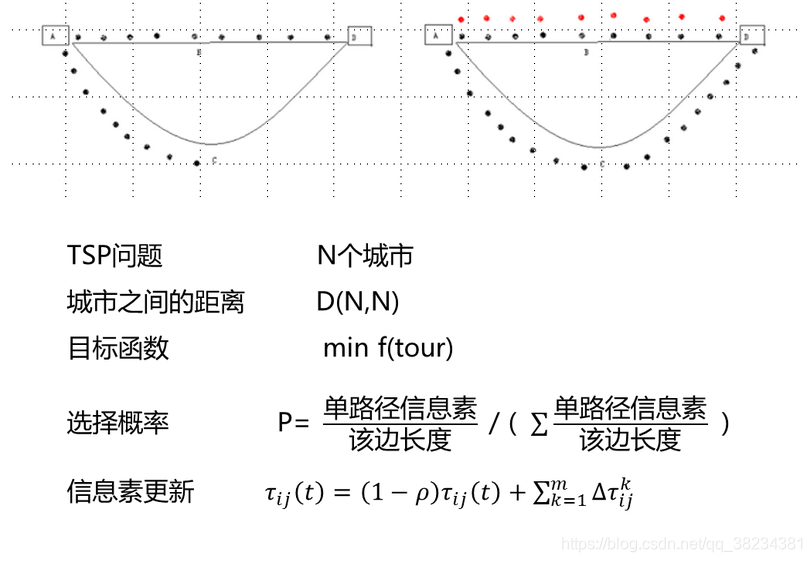
旅行商问题(Traveling Saleman Problem，TSP)是车辆路径调度问题(VRP)的特例，由于数学家已证明TSP问题是NP难题，因此，VRP也属于NP难题。旅行商问题（TSP）又译为旅行推销员问题、货郎担问题，简称为TSP问题，是最基本的路线问题，该问题是在寻求单一旅行者由起点出发，通过所有给定的需求点之后，最后再回到原点的最小路径成本。
1).经典精确算法:穷举法、线性规划算法、动态规划算法、分支定界算法等运筹学中的传统算法，这些算法复杂度一般都很大，只适用于求解小规模问题。
2).近似算法：当问题规模较大时，其所需的时间成级数增长，这是我们无法接受的，算法求解问题的规模受到了很大的限制，一个很自然的想法就是牺牲精确解法中的最优性，去寻找一个好的时间复杂度我们可以容忍的，同时解的质量我们可以接受的算法．基于这一思想所设计出的算法统称为近似算法。如插入算法，最邻近算法等。
3).智能算法：随着科学技术和生产的不断发展，许多实际问题不可能在合理的时间范围内找到全局最优解，这就促使了近代最优化问题求解方法的产生。随着各种不同搜索机制的启发式算法相继出现，如禁忌搜索、遗传算法、模拟退火算法、人工神经网络、进化策略、进化编程、粒子群优化算法、蚁群优化算法和免疫计算等。

        蚁群算法是受到对真实蚂蚁群觅食行为研究的启发而提出。生物学研究表明：一群相互协作的蚂蚁能够找到食物和巢穴之间的最短路径,而单只蚂蚁则不能。生物学家经过大量细致观察研究发现,蚂蚁个体之间的行为是相互作用相互影响的。蚂蚁在运动过程中,能够在它所经过的路径上留下一种称之为信息素的物质,而此物质恰恰是蚂蚁个体之间信息传递交流的载体。

终止条件             1，最大迭代次数
                           2，趋同
                           3，运行时间
蚁群算法处理的都是离散问题（城市都是离散的），对于连续问题（比如求一个实数）很难操作，如果是一个实数，可参考的操作方式如下：

蚁群算法演示程序：

% 初始数据输入
x=[82 91 12 92 63 9 28 55 96 97 15 98 96 49 80 14 42 92 80 96];   % 坐标点x坐标
y=[66 3 85 94 68 76 75 39 66 17 71 3 27 4 9 83 70 32 95 3];     % 坐标点y坐标
% x=[1304,3639,4177,3712,3488,3326,3238,4196,4312,4386,3007,2562,2788,2381,1332,3715,3918,4061,3780,3676,4029,4263,3429,3507,3394,3439,2935,3140,2545,2778,2370];
% y=[2312,1315,2244,1399,1535,1556,1229,1004,790,570,1970,1756,1491,1676,695,1678,2179,2370,2212,2578,2838,2931,1908,2367,2643,3201,3240,3550,2357,2826,2975];
[X1,X2]=meshgrid(x,x);
[Y1,Y2]=meshgrid(y,y);
% 建立城市坐标
D=sqrt((X1-X2).^2+(Y1-Y2).^2);  % 两点之间距离
N=numel(x);   % 一共有多少个城市 
MaxIt=300;      % 最大迭代次数
nAnt=40;        % 蚂蚁的个数（种群数量）

tau=ones(N,N);   % 初始信息素
eta=1./D;        % 启发因子矩阵,也就是距离的倒数，用于对转移概率的修正
rho=0.05;       % 挥发率 
Tour=zeros(nAnt,N);% 用于记录路径
Cost=zeros(nAnt,1);% 用于记录路径总长度
BestCost=inf; % 最佳路径长度
BestCostALL=Inf(MaxIt,1); % 每一代的最佳路径长度
for iter=1:MaxIt   % 迭代次数
    for kAntID=1:nAnt   % 每个蚂蚁分别计算
        Tour(kAntID,1)=randi([1 N]);  % 1到N之间的任意一个整数，作为起始点
        for itourcity=2:N   % 需要走的城市路径下标，因为第一个已经有了，所以这里从2开始编号
            lastcityID=Tour(kAntID,itourcity-1); % 记录上一个城市
            P=tau(lastcityID,:).*eta(lastcityID,:);% 转移概率
            P(Tour(kAntID,1:itourcity-1))=0;   % 禁忌表，已经走过的概率设置为0
            P=P/sum(P);  % 归一化
            r=rand;
            C=cumsum(P); % 可以画数轴，辅助理解    
            j=find(r<=C,1);   % 根据之前概率分布随机选择一个信息素多（概率大）的城市
            Tour(kAntID,itourcity)=j;  % 记录蚂蚁走过的城市
        end
        Ttemp=[Tour(kAntID,:)' Tour(kAntID,[2:end 1])'];  % 当前蚂蚁各段路径的起点终点
        L=0;   % 总路径长度初始值
        for i=1:N
            L=L+D(Ttemp(i,1),Ttemp(i,2)); % 将各段路径长度加起来
        end
        Cost(kAntID)=L;   % 总的路径长度
        if Cost(kAntID)<BestCost    % 如果路径更短
            BestTour=Tour(kAntID,:);  % 更新最佳路径
            BestCost=Cost(kAntID);    % 更新最佳路径长度
        end
    end
    % 更新信息素
    for kAntID=1:nAnt
        tour=[Tour(kAntID,:) Tour(kAntID,1)]; %  首尾相连的完整路径
        for itourcity=1:N
            i=tour(itourcity);
            j=tour(itourcity+1);
            tau(i,j)=tau(i,j)+1/Cost(kAntID);  
            % 原有信息素，加上新增加的信息素，新增加的信息素按照总长度的倒数来计算
        end
    end
    % 信息素挥发
    tau=(1-rho)*tau;
    % 存储每代最优结果
    BestCostALL(iter)=BestCost;
    
    % 显示迭代结果信息
    disp(['Iteration ' num2str(iter) ': Best Cost = ' num2str(BestCostALL(iter))]);
    
    % 绘制中间结果图
    PlotSolution(BestTour,x,y);
    pause(0.01); % 暂停0.01秒
    
end
% 结果
figure;
plot(BestCostALL,'LineWidth',2);
xlabel('Iteration');
ylabel('Best Cost');
grid on;


function PlotSolution(tour,x,y)

    tour=[tour tour(1)];
    
    plot(x(tour),y(tour),'k-o',...
        'MarkerSize',10,...
        'MarkerFaceColor','y',...
        'LineWidth',1.5);
    
    xlabel('x');
    ylabel('y');
    
    axis equal;
    grid on;
    
	alpha = 0.1;
	
    xmin = min(x);
    xmax = max(x);
    dx = xmax - xmin;
    xmin = floor((xmin - alpha*dx)/10)*10;
    xmax = ceil((xmax + alpha*dx)/10)*10;
    xlim([xmin xmax]); % x轴的范围
    
    ymin = min(y);
    ymax = max(y);
    dy = ymax - ymin;
    ymin = floor((ymin - alpha*dy)/10)*10;
    ymax = ceil((ymax + alpha*dy)/10)*10;
    ylim([ymin ymax]); % y轴的范围
    
    
end

时间序列
时间序列是按时间顺序排列的、随时间变化且相互关联的数据序列。分析时间序列的方法构成数据分析的一个重要领域，即时间序列分析。
时间序列根据所研究的依据不同，可有不同的分类。
按所研究的对象的多少分，有一元时间序列和多元时间序列。
按时间的连续性可将时间序列分为离散时间序列和连续时间序列两种。
按序列的统计特性分，有平稳时间序列和非平稳时间序列。
按时间序列的分布规律来分，有高斯型时间序列和非高斯型时间序列。
时间序列分析方法概述
时间序列中常用预测技术  一个时间序列是一组对于某一变量连续时间点或连续时段上的观测值。
1.  移动平均法 (MA)
    1.1. 简单移动平均法
设有一时间序列y1,y2,..., 则按数据点的顺序逐点推移求出N个数的平均数，即可得到一次移动平均数.
    1.2 趋势移动平均法  
当时间序列没有明显的趋势变动时，使用一次移动平均就能够准确地反映实际情况，直接用第t周期的一次移动平均数就可预测t+1周期之值。
时间序列出现线性变动趋势时，用一次移动平均数来预测就会出现滞后偏差。修正的方法是在一次移动平均的基础上再做二次移动平均，利用移动平均滞后偏差的规律找出曲线的发展方向和发展趋势，然后才建立直线趋势的预测模型。故称为趋势移动平均法。
2.  自回归模型(AR)
AR模型是一种线性预测，即已知N个数据，可由模型推出第N点前面或后面的数据（设推出P点）.
本质类似于插值，其目的都是为了增加有效数据，只是AR模型是由N点递推，而插值是由两点（或少数几点）去推导多点，所以AR模型要比插值方法效果更好。
3. 自回归滑动平均模型(ARMA)
其建模思想可概括为：逐渐增加模型的阶数，拟合较高阶模型，直到再增加模型的阶数而剩余残差方差不再显著减小为止。
4. GARCH模型
回归模型。除去和普通回归模型相同的之处，GARCH对误差的方差进行了进一步的建模。特别适用于波动性的分析和预测。
5. 指数平滑法
移动平均法的预测值实质上是以前观测值的加权和，且对不同时期的数据给予相同的加权。这往往不符合实际情况。
指数平滑法则对移动平均法进行了改进和发展，其应用较为广泛。
基本思想都是：预测值是以前观测值的加权和，且对不同的数据给予不同的权，新数据给较大的权，旧数据给较小的权。
根据平滑次数不同，指数平滑法分为：一次指数平滑法、二次指数平滑法和三次指数平滑法等

data = iddata(sin(0.1*[1:100])',[]); % iddata的作用是将一组数据转化为iddata类型的数据
plot(data) % 可以直接画图

sys = ar(data,2) % 建立ar模型，第二个参数表示每一个新的数跟过去的两个数相关

K = 100; % 预测后100个点
p = forecast(sys,data,K);


plot(data,'b',p,'r'), legend('measured','forecasted')

forecast(sys,data,K) % 也可以不调用plot，直接用这句