深度篇——神经网络(三) 网络拓扑与训练神经网络

万道一

于 2020-02-06 19:04:51 发布

阅读量1.9k

点赞数 2

分类专栏： AI章文章标签：深度学习

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/qq_38299170/article/details/104118921

版权

本文深入探讨了神经网络的网络拓扑，包括单层和多层网络结构，并详细阐述了训练神经网络的过程，涉及前向传播、反向传播、链式法则和梯度下降法。通过实例解释了如何计算损失函数和更新权重，为理解神经网络的训练机制提供了清晰的指导。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

返回主目录

返回神经网络目录

上一章：深度篇——神经网络(二) ANN与DNN 和常用激活函数

下一章：深度篇——神经网络(四) 细说调优神经网络

本小节，细说网络拓扑与训练神经网络，下一小节细说调优神经网络

二. ANN 与 DNN

3. 网络拓扑

(1). 单层网络

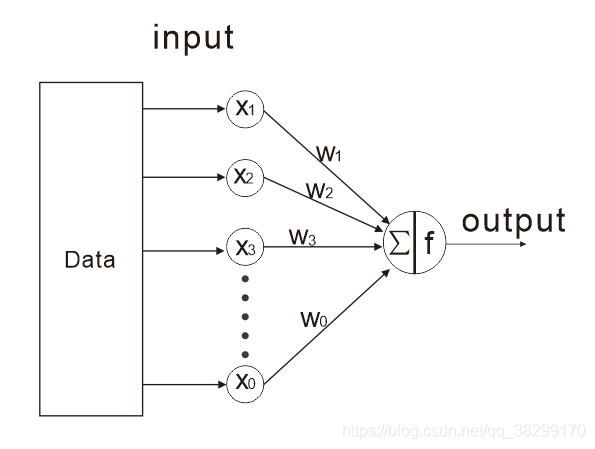
(2). 多层网络

多层网络至少有 1 个 hidden 层，也可以有多个 hidden 层。有 bias 值，可以让函数不必一定要经过原点。

(3). 无论是 ANN，还是 DNN，网络连接都是全连接。

output 层的激活函数与 hidden 层的激活函数可以相同，也可以不同，根据需求而定。output 层可以是单值输出，也可以是多值输出。

4. 训练神经网络

(1). 训练神经网络的两个阶段

①. 前向阶段

前向阶段即正向传播

正向传播根据数据集和激活函数，当前的 $\large w$ 值，计算出 loss 损失函数

②. 后向阶段

后向阶段即反向传播

反向传播利用链式法则对 $\large w$ 进行求导，代入数据集的值，求出梯度 $\large g$

③. 链式法则

若函数 $\large u = \varphi (t), \; v = \psi (t)$ 在点 $\large t$ 上可导， $\large z = f(u, v)$ 则

$\large \frac{\partial z}{\partial t} = \frac{\partial z}{\partial u} \times \frac{\partial u}{\partial t} + \frac{\partial z}{\partial v} \times \frac{\partial v}{\partial t}$

④. 栗子

a. 栗一

有 $\large f(x, y, z) = (x + y) \cdot z$ ，且 $\large x = -2, y = 5, z = -4$ 。

解：令 $\large q = x + y$ ，则

最低0.47元/天解锁文章

评论 1

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。