【poj3070】 Fibonacci 【矩阵乘法】

最新推荐文章于 2021-09-24 14:28:56 发布

Yang_Z_H

最新推荐文章于 2021-09-24 14:28:56 发布

阅读量341

点赞数 2

分类专栏：矩阵

本文链接：https://blog.csdn.net/qq_38465092/article/details/77165552

版权

矩阵专栏收录该内容

2 篇文章 0 订阅

订阅专栏

讲解：点击打开链接

Fibonacci

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 15917		Accepted: 11188

Description

In the Fibonacci integer sequence, F₀ = 0, F₁ = 1, and F_n = F_n_{− 1} + F_n_{− 2} for n ≥ 2. For example, the first ten terms of the Fibonacci sequence are:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …

An alternative formula for the Fibonacci sequence is

Given an integer n, your goal is to compute the last 4 digits of F_n.

Input

The input test file will contain multiple test cases. Each test case consists of a single line containing n (where 0 ≤ n ≤ 1,000,000,000). The end-of-file is denoted by a single line containing the number −1.

Output

For each test case, print the last four digits of F_n. If the last four digits of F_n are all zeros, print ‘0’; otherwise, omit any leading zeros (i.e., print F_n mod 10000).

Sample Input

Sample Output

Hint

As a reminder, matrix multiplication is associative, and the product of two 2 × 2 matrices is given by

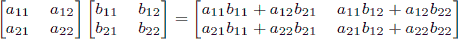Also, note that raising any 2 × 2 matrix to the 0th power gives the identity matrix:

题目描述
斐波那契数列是由如下递推式定义的数列
F0=0
F1=1
Fn+1=Fn+1+Fn
求这个数列第n项的值对 104 取余后的结果。
限制条件
⋅ 0⩽n⩽1016

我也是刚刚才搞懂了矩阵乘法(如果你不知道什么是矩阵乘法的话,右转百度百科)，于是来应用一下新知识，如有表述不到位的地方请见谅。
下面进入正文

首先，我们先介绍一下对于斐波那契数列如何求解。把斐波那契数列的递推式表示成矩阵就得到下面的式子
(Fn+2Fn+1)= (1110) (Fn+1Fn)

我们发现式子里有个固定的矩阵 (1110)

记这个矩阵为A，则有
(Fn+1Fn)= An (F1F0)= An (10)

因此只要求出 An 就可以求出 Fn 了。关于 An 的计算我们可以采用类似快速幂的算法,在 O(logn) 时间里求出第n项的值。（转自：点击打开链接）

#include<cstdio>
 
int n,a[2][2],b[2][2];
 
void mul(int a[2][2],int b[2][2],int ans[2][2])
{
    int t[2][2];
    for (int i=0;i<2;i++)
        for (int j=0;j<2;j++) 
		{
            t[i][j]=0;
            for (int k=0;k<2;k++) 
			t[i][j]=(t[i][j]+a[i][k]*b[k][j])%10000;
        }
    for (int i=0;i<2;i++)
        for (int j=0;j<2;j++) 
		ans[i][j]=t[i][j];
}
void pow(int k) 
{
    while (k) 
	{
        if (k%2==1) 
		mul(a,b,b);
        k/=2;
        mul(a,a,a);
    }
}
int main() 
{
    while (scanf("%d",&n)!=EOF) 
	{
        if (n==-1) 
		break;
        a[0][0]=a[0][1]=a[1][0]=1;a[1][1]=0;
        
        b[0][0]=b[1][1]=1;
        b[1][0]=b[0][1]=0;
        
        pow(n);
        printf("%d\n",b[1][0]);
    }
    return 0;
}

这道题还碰见一种神奇的操作，我还没理解到底是什么规律。。

来自：（点击打开链接）

#include<stdio.h>
int a[100050];
void f() 
{
	a[0] = 0;
	a[1] = 1;
	for (int i  = 2; i <= 100050; i ++) 
	{
		a[i] = (a[i - 1] + a[i - 2]) % 10000;
	}
}
int main () 
{
	int n;
	while (scanf("%d", &n) != EOF) 
	{
		if(n == -1) break;
		f();
		printf("%d\n", a[n % 15000]);
	}
	return 0;
}