Symmetric diffeomorphic image registration with cross-correlation

Symmetric diffeomorphic image registration with cross-correlation: Evaluating automated labeling of elderly and neurodegenerative brain

摘要

 

现代神经影像学最具挑战性的问题之一是对神经变性的详细描述，量化空间和纵向萎缩模式是这一过程的重要组成部分。这些时空信号将有助于识别相关疾病，比如额颞叶痴呆(FTD)和阿尔茨海默病(AD)，它们都出现在相同的高危人群中。在此，我们发展了一种新的对称图像归一化方法(SyN)来最大限度的互相关在空间的不同同构映射，并提供了欧拉-拉格朗日方程的必要的优化。然后，我们对我们的方法进行仔细的评估。我们的评估使用金标准，人类皮层分割SyN的性能与相关的弹性方法和标准的ITK实施的Thirion 's Demons算法进行对比。新方法与两种方法相比都有优势，特别是当模板脑和目标脑之间的距离较大时，然后，我们报告了FTD和对照受试者的算法皮层标记所获得的体积与手工评分所获得的体积之间的相关性。比较表明，在三种方法中，SyN的体积测量值与专家标记得到的体积测量值相关性最强。本研究表明，SyN是一种可靠的方法，可以在MRI容积测量中对患者和高危老年人进行归一化和解剖测量。

介绍

额颞叶痴呆(FTD)的患病率可能比之前认为的要高，在65岁以下的人群中可能与阿尔茨海默病(AD)相当，由于FTD的临床检测具有挑战性，因此确定支持临床诊断的客观方法非常重要。对个别患者的MRI研究很难解释，因为老年人群中广泛存在可接受的与年龄相关的萎缩，易患痴呆症。这促使核磁共振研究，看看两者的变化率和解剖分布的变化。

人工、专家对图像结构的描绘可以在体内量化局灶性疾病的影响，并可作为神经退行性变重要研究的基础。来自图像的专家结构测量也提供了解剖学评价的金标准，然而，人工方法仍然受到标记236^3或更多体素的复杂性的严重限制。这样的工作既耗时又费钱，而能够完成这些任务的专家数量有限。第三个困难是评分者之间的差异性问题限制了人工标注的可靠性，虽然很少用于大规模数据处理，但专家的眼睛对于有限的标记任务仍然有价值，这些任务为算法评估提供了基础。

可变形图像配准算法能够在对时间敏感的临床应用(Dawant et al.， 2003)和高通量环境中有效地发挥作用，并成功地用于自动标记和测量研究任务。一个挑战是在非标准数据上的可靠表现，比如在对可能严重的神经退行性疾病的研究中。这些类型的图像违反了许多现有图像配准方法中关于小变形和/或简单强度关系的基本假设。

不同形式的图像配准算法有希望成功地解决这达变形和小变形的问题，最先进的方法还提供了完整的时空优化，对称的图像输入和允许概率相似性措施，逆一致图像配准(ICIR)是一种额外的常用方法，可以替代差分同构映射。逆一致性最初是由Thirion作为他的Demons算法的扩展而引入的，对称方法不同于ICIR的对称算法，首先，保证结果是相同的，无论输入数据的顺序，其次，使用精确的逆变换保证的差别同构。逆一致性通过在归一化优化算法中包含变分惩罚来近似对称。根据不同数据、正则化和逆一致性项的权重，一致性可能会以牺牲其他匹配条件为代价来满足(或不满足)，此外，逆一致算法使用近似的逆变换，因为逆变换本身是近似的，所以一致性项也妥协了。

在此，我们开发了一种新的对称扩散对称优化器来最大化拓扑保持映射空间中的互相关，互相关测度在医学图像配准中已有应用和更广泛的计算机视觉。然而，这一措施还没有研究的不同形态的情况。此外，它还没有被用于对称归一化或“逆一致”研究。将我们的新的归一化公式应用于互相关提供了对互相关欧拉-拉格朗日方程进行对称化的优势(或选择)。我们证明了这些对称的欧拉-拉格朗日方程只需要很少的额外计算成本就可以计算出来。然后，我们对我们的对称扩散形算法的性能进行了仔细的评估。们将该方法与弹性互相关优化器以及在仔细评估受试者间大脑注册方面表现优于其他方法的Demons算法进行了比较。配准方法

Demons

Thirion’s Demons算法(Thirion, 1996)在主体间可变形图像配准中表现良好。该方法使用近似弹性正则化器来解决光流问题，其中“移动”图像的水平集与参考或“固定”模板图像的水平集相对应。在实际应用中，该算法计算光流项，并将其加入到总位移中(初始位移为零)。然后用高斯滤波器对总位移进行平滑处理。对于多分辨率优化方案中每个分辨率的迭代次数，该过程重复进行。该方法可在Insight工具包中免费获得，并由ITK社区(www.itk.org)进行了优化。

Dawant等人使用Demons算法分割尾状核、大脑和小脑，对正常和慢性酗酒者进行形态学比较，他们对算法的评价发现，自动标记和手动标记之间存在合理的一致性。他们还展示了海马体自动标记的结果，但没有评估表现。他们的比较使用DICE统计：

它可以测量两段之间的大小和位置的差异，R1和R2。#(R)运算符计算区域内的像素个数，这个敏感的测量值在[0,1]范围内变化，取值大于一些作者认为较小结构的0.6和较大结构的0.8是比较好的。

当然，dice统计值的可接受范围高度依赖于应用程序。一个人在“金标准”数据集中所拥有的确定性，以及分段的具体使用，都决定了一个合理的操作范围。在本文中，我们的目标是使用手动分段结构作为比较自动化规范化方法的基础。在这方面，具有临界价值的是相对性能(相对于Dice统计量进行度量)。

Symmetric diffffeomorphisms

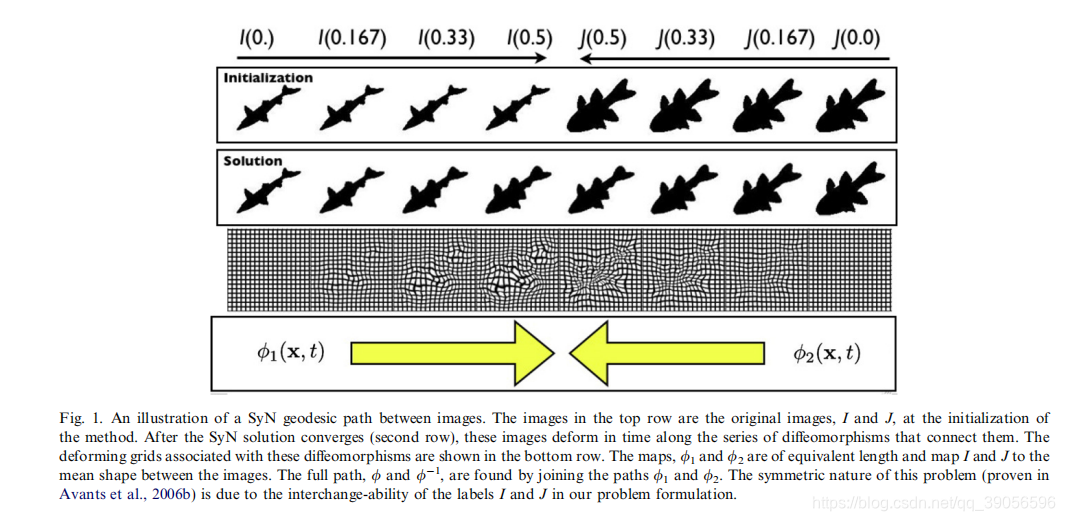
微分同态是具有可微逆的可微映射(Arnold和Khesin, 1992;阿诺德,1991)。我们通常把解限制在具有齐次边界条件的扩散纯空间扩散上,也就是说，我们假设刚性和缩放变换已经被提出来，图像边界映射到它自己,在这个空间中元素之间的最短路径称为测地线。将不同形式的方法引入医学计算机视觉(Trouv e, 1998)，旨在提供一种群论的、大变形的时空图像配准框架。大变形计算解剖学的发展现状Miller、Trouve和Younes将方法扩展到包括光度变化和使用欧拉-拉格朗日方程,然而，这些方法的标准版本，贝格的大变形同构度量匹配(LDDMM)(贝格等，2005)，没有对称地表示变换优化。它们只是在理论上是对称的，它们的实现需要并行计算。然而，通过个人的交流，我们了解到一个对称化的算子，是基于变换的雅可比矩阵，被包括在当前的发展中,然而，除了强度差之外，这些方法不能保证相似性度量的对称性。我们目前的工作扩展了Avants等人(2006a)中描述的拉格朗日差形配准技术。这种新的公式具有对称的性质，要求测地线连接两个图像，I和J，在空间的不同形式的变换和保证对称性，而不管选择的相似性衡量。这个公式解释了问题中的自然对称性:两个图像都沿着形状流形移动。对称微分同构保证了测地线路径概念固有的两个特性:从I到J的路径和J到I路径是一样的，不管相似度或优化参数。对于距离估计，对称性是必需的，无论哪一个图像是运动的还是固定的。

我们的方法的独特之处在于，它通过在优化中直接包含可逆性约束来保证离散域的亚像素级精度和可逆变换。虽然理论上可以保证微分同构是可逆的，但插补误差会导致可逆性误差随插补步数的增加而线性增加。另一方面，我们的解决方案，通过利用由微分同态保证的可逆性来直接最小化这个误差。最后，该方法在单处理器机器和处理大型数据集上非常有效。

我们定义在区域一个微分同胚,通常，将图像I通过转换为新的坐标系时，这表明
I被定义的映射向前弯曲。也可以使用更标准的反向扭曲策略，通过，达到同样的变形。这些变换的参数是时间t，空间坐标x，速度场，，平方可积的连续向量场，对应的地图，通过对速度场进行时间积分得到。，距离是，L定义了使速度正则化的线性算子。正则化，通过线性微分算子，例如这种差别同构在空间和时间上都给出了一个稠密的映射。

 

 

未完待续.....