流体模拟（二）
光滑核函数：
sph中涉及的光滑核可以理解为：在一定的光滑核半径内，所受的力受距离权重的影响，距离越近所受影响越大。其表现形式如图所示。
这里我们便可以将流体看成一个个粒子的集合，每一个粒子都受周围一定范围内的其他粒子影响。该粒子的最终属性都由周围所有粒子的加权值来决定。如下图所示：
我们在流体中随机选择一个粒子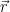,在光滑核半径h范围内有多个粒子，位置分别是
，…
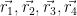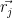，则该处某项属性A的累加公式为：
其中Aj是要累加的某种属性（如密度，压力，粘度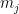），和
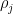是周围粒子的质量和密度，
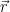是该粒子的位置，h是光滑核半径。函数W就是光滑核函数。
光滑核函数两个重要属性，首先一定是偶函数，也就是W(−r)=W(r)，第二，是“规整函数”，也就是。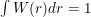
SPH推导过程
我们假设流体中一个位置为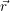的点，此处的密度为ρ(
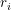)、压力为p(
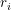)、速度为u⃗ (
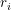)，那么我们可以根据上一篇2.8的公式，可以推导出此处的加速度a⃗ (
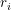)为：
对于SPH算法来说，基本流程就是这样，根据光滑核函数逐个推出流体中某点的密度，压力，速度相关的累加函数，进而推导出此处的加速度，从而模拟流体的运动趋势，下面依次分析密度，压力，粘度的求解。
密度
根据公式3.1，用密度ρ代替A，可以得到
计算使用的光滑核函数称为Poly6函数，具体形式为:
其中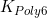 是一个固定的系数，根据光滑核的规整属性，通过积分计算出这个系数的具体值，在2D情况下，在极坐标中计算积分：
3D情况下，在球坐标中计算:
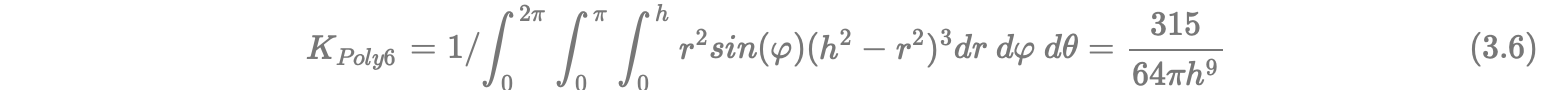
由于所有粒子的质量相同都是m，所以在3D情况下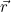，处的密度计算公式最终为：
压力
根据2.5的公式代入3.1便可以求解压力，在位置之处的由压力产生的作用力的计算公式为：
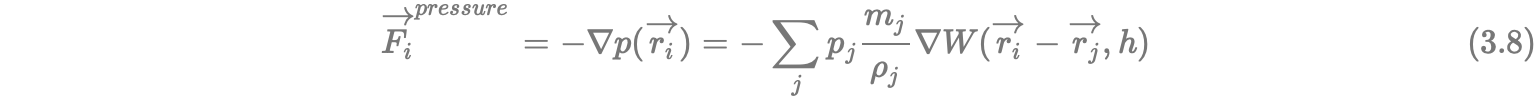
由于位于不同压强区的两个粒子之间的作用力不等，该等式是“不平衡”的。所以计算中一般使用双方粒子压强的算术平均值代替单个粒子的压力之处的由压力产生的作用力的计算公式为：
对于单个粒子产生的压力p,可以用理想气体状态方程计算：
其中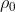是流体的静态密度，K是和流体相关的常数，只跟温度相关。压力计算中使用的光滑核函数称为Spiky函数：
在3D情况下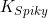，=15/(
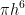)，则：
将公式3.12带入3.9，可以整理出公式3.2中压力产生的加速度部分：
粘度
公式3.2中最后一部分，由粘度产生的作用力：
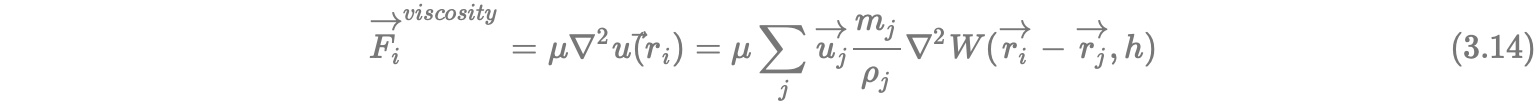
这个公式同样有“不平衡”的问题，考虑到公式中的速度其实并不是绝对速度，而是粒子间的相对速度，所以这个公式的正确写法应该是：
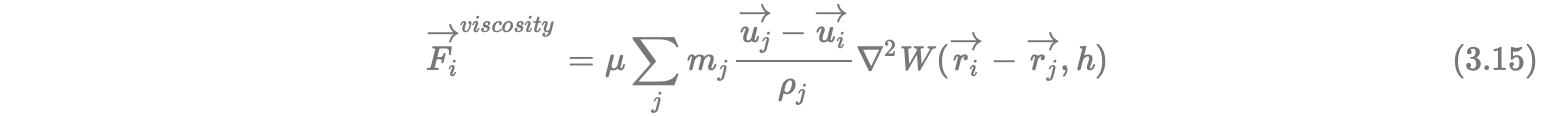
其中的光滑核函数形式如下：
在3D情况下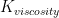，=15/(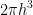
)。
由此可得到公式3.2的粘度部分：
到这里，根据我们已经获得的数据，把公式3.13和3.17带入3.2，我们就可以计算最后的加速度了：
到这里，我们SPH部分的数学公式都在这里，我们接下来只要用他们，就能模拟出水粒子的运动轨迹了。
在刚开始学习SPH的时候，我是从这里https://thecodeway.com/，了解到SPH的总体数学思路，虽然和后来看论文里，有些公式有些许不同，不过原理都是一模一样的。
接下来就需要创建专门的数据结构，以及算法来处理粒子间的关系来建立一个流体模拟的系统了。
651
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
