树状数组其实是在数组上模拟树的结构,一般用于解决区间问题,然而对于区间问题而言,最强大的莫过于线段树了。不过树状数组相比线段树而言,无论是代码量,还是常数都要低很多,因此还是很强大的。
我们用一个求和问题引入树状数组:如何快速求解A[i]~A[j]的和。
事实上,使用前缀和数组,我们可以得到:
代码:
#include<bits/stdc++.h>
using namespace std;
const int MaxN = 10010;
int prefixSum[MaxN];
int getSum(int i,int j){
return prefixSum[j] - prefixSum[i-1];
}
int main(){
int n, m, i, j, k;
cin >> n >> m;
for(i=1; i<=n; ++i){
cin >> prefixSum[i];
prefixSum[i] += prefixSum[i-1];
}
for(k=1; k<=m; ++k){
cin >> i >> j;
cout << getSum(i , j) << endl;
}
return 0;
} 虽然前缀和数组构建简单,并且计算迅速,但是前缀和数组很难同时用于修改和查询。
而对于修改而言,最简单的修改莫过于构建差分数组,即构建。在差分数组下(需要预设
),我们想要修改任意区间内的值,只需要修改端点处即可。假设我们有需要给A[i]~A[j]的所有元素都加上delta,传统的做法是遍历A[i]~A[j],然后依次修改。而差分数组下,我们只需要让
,但是差分数组上需要求某一个值
需要遍历,即
为了缓和前缀和数组与差分数组一个操作很快另一个操作很慢的尴尬,树状数组做了一个折中。
树状数组使用了二进制的思想,让每一个2的次幂区间负责计算它所覆盖的区间和,并且使用2的次幂的区间进行整体上的分割。这个可能比较难理解,我们以1-8为例说明一下,(下面有图,图上展示了二次幂区间分解,可以对照着看)。
对1:它是2^0,因此它负责从 起点~自己 即 1~1
对2:它是2^1,因此它负责从 起点~自己 即1~2
对3:它不是2的次幂,但它和左边最近的二次幂区间(1~2)距离为1(2^0),因此它负责从 当前二次幂区间起点~自己 即 3~3
对4:它是2^2,因此它负责从 起点~自己 即1~4
对5:它不是2的次幂,但它和左边最近的二次幂区间(1~4)距离为1(2^0),因此它负责从 当前二次幂区间起点~自己 即5~5
对6:它不是2的次幂,但是它和左边最近的二次幂区间(1~4)距离为2(2^1),因此它负责从 当前二次幂区间起点~自己 即5~6
对于7来说,不是2的次幂,但是它和左边最近的二次幂区间(5~6)距离为1(2^0),因此它负责从 当前二次幂区间起点~自己 即7~7
对于8来说,它是2^3,因此它负责从 起点~自己 即1~8
当我们想求A[1]~A[22]的和的时候,我们可以通过二次幂区间分解的方式,得到
上述式中,Tree[16]维护了A[1]~A[16]的和(1~16为2^4区间),Tree[20]维护了A[17]~A[20]的和,Tree[22]维护了A[21]~A[22]的和,而我们可以惊喜地发现,22的二进制为(10110),三个1各自所在的权值为16、4、2,完美地和我们的数组对应。而一个数在二进制下,最多会有logn个1,所以树状数组的操作复杂度可以变为O(logn)。
来看一个树状数组的结构图:

在上图中,树状数组构建出来的新数组C[i],应满足如下式子:
| C[1] = A[1] |
| C[2] = A[1] + A[2] |
| C[3] = A[3] |
| C[4] = A[1] + A[2] + A[3] + A[4] |
| C[5] = A[5] |
| C[6] = A[5] + A[6] |
| C[7] = A[7] |
| C[8] = A[7] + A[8] |
这样做的意义是什么呢?我们可以发现,当我们这样构建树状数组的时候,我们就可以按照二进制分解的方式,求得区间和:
此处还要介绍一个算法叫做lowbit(x):通过上面的分析我们已经知道,树状数组其实就是通过几个二次幂长度的区间对大区间进行分解。而每一个用于大区间分解的二次幂区间的长度对应了区间终点的二进制中1的权值。
以22为例,22的二进制表示为(10110),而第一个区间A[21]~A[22]的长度正好就是最右边的1的权值,从而我们知道Tree[22]在答案中。此时已经考虑了A[21]~A[22]的我们,应该考虑剩下的A[1]~A[20],20的二进制为(10100),是由(10110)-(00010)得到。重复这个过程,直到区间端点变为0,累计中间的过程值,此时我们就求出了A[1]~A[22]。
现在的问题是,我们怎么快速地获取任意一个数x(x>0)在二进制表示下的最右边的1对应的权值。这需要用到补码的知识,对于一个正数而言,它的补码就是本身,而它的相反数的补码是正数的原码,符号位取反(由0->1),数值位取反后整体加1。假设x(x>0)的补码为0...1000...000,当取-x的补码时,就会变成1...0111...111+1=1...1000...000,二者取&就可以拿到0...1000...000。(高位必定每一位都相反)
举个例子,对于整数10,在8位整型(位数只是为了简化问题)表示下为:00001010,它的补码-10为11110101+1=11110110,取余后得到00000010(补码的设计初衷就是为了让符号位参与运算,简化电路设计)。
树状数组的模板:
#include<bits/stdc++.h>
using namespace std;
const int MaxN = 10010;
int Tree[MaxN];
int lowbit(int x){
return x & (-x);
}
void update(int i,int n,int delta){
while(i <= n){
Tree[i]+=delta;
i += lowbit(i);
}
}
int getSum(int i){
int sum=0;
while(i){
sum += Tree[i];
i -= lowbit(i);
}
return sum;
}
int main(){
int n, i, j, k;
cin >> n ;
for(i=1; i<=n; ++i){
cin >> Tree[i];
update(i,n,Tree[i]);
}
return 0;
} 树状数组可以用来解决的问题有三类:(单点修改单点查询不就是直接原地操作嘛=-=)
1.单点修改,区间查询
树状数组可以帮助我们在O(logn)的复杂度内求得A[1]~A[i]的和,当我们需要求解A[L]~A[R]的时候,我们只需要求A[1]~A[R]-A[1]~A[L]。
HDU - 1166 敌兵布阵
描述
C国的死对头A国这段时间正在进行军事演习,所以C国间谍头子Derek和他手下Tidy又开始忙乎了。A国在海岸线沿直线布置了N个工兵营地,Derek和Tidy的任务就是要监视这些工兵营地的活动情况。由于采取了某种先进的监测手段,所以每个工兵营地的人数C国都掌握的一清二楚,每个工兵营地的人数都有可能发生变动,可能增加或减少若干人手,但这些都逃不过C国的监视。
中央情报局要研究敌人究竟演习什么战术,所以Tidy要随时向Derek汇报某一段连续的工兵营地一共有多少人,例如Derek问:“Tidy,马上汇报第3个营地到第10个营地共有多少人!”Tidy就要马上开始计算这一段的总人数并汇报。但敌兵营地的人数经常变动,而Derek每次询问的段都不一样,所以Tidy不得不每次都一个一个营地的去数,很快就精疲力尽了,Derek对Tidy的计算速度越来越不满:"你个死肥仔,算得这么慢,我炒你鱿鱼!”Tidy想:“你自己来算算看,这可真是一项累人的工作!我恨不得你炒我鱿鱼呢!”无奈之下,Tidy只好打电话向计算机专家Windbreaker求救,Windbreaker说:“死肥仔,叫你平时做多点acm题和看多点算法书,现在尝到苦果了吧!”Tidy说:"我知错了。。。"但Windbreaker已经挂掉电话了。Tidy很苦恼,这么算他真的会崩溃的,聪明的读者,你能写个程序帮他完成这项工作吗?不过如果你的程序效率不够高的话,Tidy还是会受到Derek的责骂的.
Input
第一行一个整数T,表示有T组数据。
每组数据第一行一个正整数N(N<=50000),表示敌人有N个工兵营地,接下来有N个正整数,第i个正整数ai代表第i个工兵营地里开始时有ai个人(1<=ai<=50)。
接下来每行有一条命令,命令有4种形式:
(1) Add i j,i和j为正整数,表示第i个营地增加j个人(j不超过30)
(2)Sub i j ,i和j为正整数,表示第i个营地减少j个人(j不超过30);
(3)Query i j ,i和j为正整数,i<=j,表示询问第i到第j个营地的总人数;
(4)End 表示结束,这条命令在每组数据最后出现;
每组数据最多有40000条命令
Output
对第i组数据,首先输出“Case i:”和回车,
对于每个Query询问,输出一个整数并回车,表示询问的段中的总人数,这个数保持在int以内。
Sample Input
1
10
1 2 3 4 5 6 7 8 9 10
Query 1 3
Add 3 6
Query 2 7
Sub 10 2
Add 6 3
Query 3 10
End Sample Output
Case 1:
6
33
59树状数组裸题,直接套模板即可,注意新的一轮需要将数据初始化。
代码:
#include<bits/stdc++.h>
using namespace std;
const int MaxN = 50010;
int Tree[MaxN];
int lowbit(int x){
return x & (-x);
}
void update(int i,int n,int delta){
while(i <= n){
Tree[i] += delta;
i += lowbit(i);
}
}
int getSum(int i){
int sum=0;
while(i){
sum += Tree[i];
i -= lowbit(i);
}
return sum;
}
int main(){
int n, i, j, k, T ,val;
string op;
cin >> T ;
for(int t=1 ; t<=T ; ++t){
memset(Tree, 0, sizeof(Tree));
cin >> n;
for(i=1; i<=n; ++i){
cin >> val;
update(i, n, val);
}
cout<<"Case "<<t<<":"<<endl;
while(cin >> op ){
switch( op[0] ){
case 'A':cin >> i >> j;
update(i , n, j);
break;
case 'Q':cin >> i >> j;
cout<<getSum(j)-getSum(i-1)<<endl;
break;
case 'S':cin >> i >> j;
update(i , n, -j);
break;
case 'E':goto label;
}
}
label:;
}
return 0;
} 2.区间修改,单点查询
现在我们知道了单点修改,区间查询的做法,那么对于区间修改,单点查询应该怎么做呢。首先对于区间修改,我们知道最简单的方式就是构建差分数组,并且差分数组的性质就是
这是一个求和的过程,而我们已经知道,树状数组可以加速求和的过程,因此我们可以把差分数组建成树状数组。在更新的时候,原来在差分数组上,是使得Diff[L] += delta,Diff[R+1] -= delta。而在差分数组上,需要依照树状数组的方式进行更新。
洛谷P3368 【模板】树状数组 2
提交42.25k
通过22.07k
时间限制1.00s
内存限制125.00MB
题目描述
如题,已知一个数列,你需要进行下面两种操作:
1.将某区间每一个数数加上 xx;
2.求出某一个数的值。
输入格式
第一行包含两个整数 N、M,分别表示该数列数字的个数和操作的总个数。
第二行包含 N 个用空格分隔的整数,其中第 i 个数字表示数列第 i 项的初始值。
接下来 MM 行每行包含 2 或 4个整数,表示一个操作,具体如下:
操作 1: 格式:1 x y k 含义:将区间 [x,y]内每个数加上 k;
操作 2: 格式:2 x 含义:输出第 x 个数的值。
输出格式
输出包含若干行整数,即为所有操作 2 的结果。
输入输出样例
输入 #1复制
5 5
1 5 4 2 3
1 2 4 2
2 3
1 1 5 -1
1 3 5 7
2 4输出 #1复制
6
10#include<bits/stdc++.h>
using namespace std;
const int MaxN = 500010;
typedef long long ll;
ll Tree[MaxN],Arr[MaxN];
int lowbit(int x){
return x & (-x);
}
inline int read(){
int s=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;
}
void update(int i,int n,ll delta){
while(i <= n){
Tree[i] += delta;
i += lowbit(i);
}
}
ll getSum(int i){
ll sum=0;
while(i){
sum += Tree[i];
i -= lowbit(i);
}
return sum;
}
int main(){
int N, M, i, x, y, k ,op;
N = read();M = read();
for(i=1; i<=N; ++i){
Arr[i] = read();
update(i, N, Arr[i] - Arr[i-1]);
}
for(i=1; i<=M; ++i){
op = read();
if(op & 1){
x = read();y = read();k = read();
update(x, N, k);
update(y+1 , N , -k);
}else{
x = read();
cout<<getSum(x)<<endl;
}
}
return 0;
} 3.区间修改,区间查询
首先为了能够做到快速修改,我们依旧是把差分数组建成树状数组。现在我们来看看,在差分数组上,我们要怎么在差分数组上求解区间和问题。为了简化问题,我们先讨论A[1]~A[n]的区间和。
首先由于差分数组的构成方式,我们有
那么区间和A[1]~A[n]就可以表示为
在这个式子中,n是一个变动的量,因此就没办法维护,因为对于不同的n,需要维护的值也就不一样,因此我们需要想办法消去这个n,让我们试试用n*A[n]减去它:
现在我们得到了这个新的表达式中是不再含有变量n的,而且我们知道n*A[n]-res=A[1]~A[n]。于是我们需要维护一个新的数组D[i],并且有D[i]=(i-1)*C[i],n*A[n] - res = A[1]~A[n]。
差分数组依旧按照C[L] += delta,C[R+1] -= delta的方式更新,而到了D[i]就不一样了。因为存在D[i]=(i-1)*C[i],因此C[L] += delta,反映到D[L]上,应该是D[L] += (L-1)*delta,同理C[R+1] -= delta反映到D[R+1]上是D[R+1] -= (R+1-1)*delta=R*delta。
POJ 3468
链接:http://poj.org/problem?id=3468
A Simple Problem with Integers
| Time Limit: 5000MS | Memory Limit: 131072K | |
| Total Submissions: 183967 | Accepted: 56699 | |
| Case Time Limit: 2000MS | ||
Description
You have N integers, A1, A2, ... , AN. You need to deal with two kinds of operations. One type of operation is to add some given number to each number in a given interval. The other is to ask for the sum of numbers in a given interval.
Input
The first line contains two numbers N and Q. 1 ≤ N,Q ≤ 100000.
The second line contains N numbers, the initial values of A1, A2, ... , AN. -1000000000 ≤ Ai ≤ 1000000000.
Each of the next Q lines represents an operation.
"C a b c" means adding c to each of Aa, Aa+1, ... , Ab. -10000 ≤ c ≤ 10000.
"Q a b" means querying the sum of Aa, Aa+1, ... , Ab.
Output
You need to answer all Q commands in order. One answer in a line.
Sample Input
10 5
1 2 3 4 5 6 7 8 9 10
Q 4 4
Q 1 10
Q 2 4
C 3 6 3
Q 2 4
Sample Output
4
55
9
15Hint
The sums may exceed the range of 32-bit integers.
思路:大致题意是有两种操作,一个是为给定区间上的所有数都加上一个值,一个是求出一个区间的所有数的和,很显然这就是区间修改,区间求和问题。
代码:
#include<cstdio>
using namespace std;
const int MaxN = 1000010;
typedef long long ll;
ll C[MaxN],D[MaxN];
int lowbit(int x){
return x & (-x);
}
inline ll read(){
ll s=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;
}
void update(ll Tree[],ll i,ll n,ll delta){
while(i <= n){
Tree[i] += delta;
i += lowbit(i);
}
}
ll getSum(ll Tree[],ll i){
ll sum=0;
while(i>0){
sum += Tree[i];
i -= lowbit(i);
}
return sum;
}
int main(){
ll N, Q, i, L, R, delta ,pre=0, p;
char op;
N = read();Q = read();
for(i=1; i<=N; ++i){
p = read();
update(C, i, N, p-pre);
update(D, i, N, (i-1) * (p-pre));
pre = p;
}
for(i=1; i<=Q; ++i){
op = getchar();
if( op == 'Q'){
L = read(); R = read();
printf("%lld\n",R*getSum(C, R) - getSum(D, R) - (L-1)*getSum(C, L-1) + getSum(D, L-1));
}else{
L = read(); R = read(); delta = read();
update(C, L, N, delta);
update(C, R+1, N, -delta);
update(D, L, N, (L-1) * delta);
update(D, R+1, N, R * (-delta));
}
}
return 0;
} 二维树状数组
定义二维树状数组上Tree[x][y]表示以[1,1]为左上角,[x,y]为右下角的矩阵区域中含有的有效信息个数。在更新和求和时,我们仿照一维下的做法,先按y再按x或
1.单点修改,区间查询
这种问题直接仿照一维树状数组,先更新一个维度,再更新另一个维度。一般选择先更新Y,后更新X:注意也不要对模板太过死板,有些题目可能会给出的坐标系并不是按照从左到右为X,从上到下为Y的,此时需要自行转换。
void update(int x,int y,int n,int m,int delta){
int j;
while(x<=n){
j=y;
while(j<=m){
Tree[x][j]+=delta;
j+=lowbit(j);
}
x+=lowbit(x);
}
}
int getSum(int x,int y){
int sum=0,j;
while(x){
j=y;
while(j){
sum+=Tree[x][j];
j-=lowbit(j);
}
x-=lowbit(x);
}
return sum;
}有了二维树状数组,当我们需要求[X1,Y1]为左上角,[X2,Y2]为右下角的矩形中的有效内容时,可以选择使用getSum(X2,Y2)-getSum(X1-1,Y2)-getSum(X2,Y1-1)+getSum(X1-1,Y1-1)。
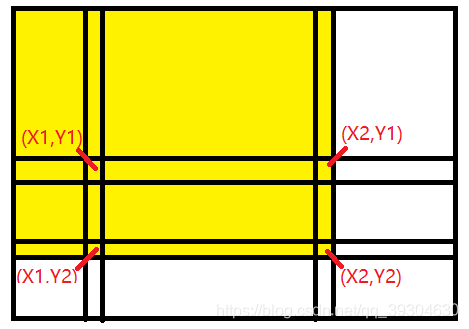
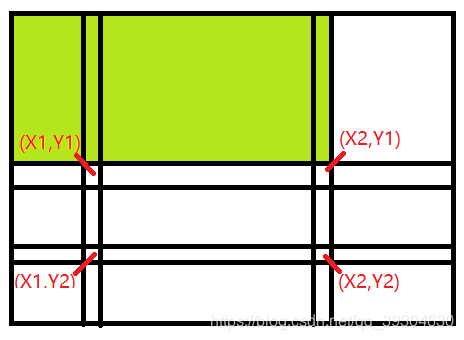
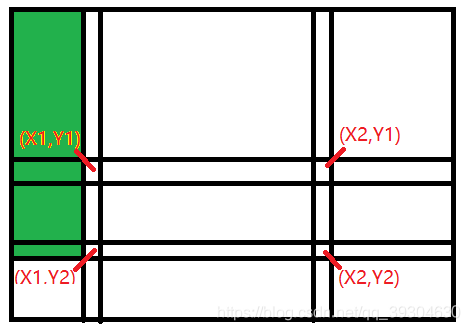
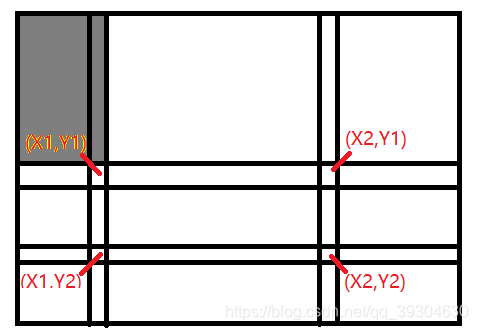
int RectSum(int X1,int Y1,int X2,int Y2){
return getSum(X2,Y2)-getSum(X1-1,Y2)-getSum(X2,Y1-1)+getSum(X1-1,Y1-1);
}POJ 1195 Mobile phones
| Time Limit: 5000MS | Memory Limit: 65536K | |
| Total Submissions: 25083 | Accepted: 11442 |
Description
Suppose that the fourth generation mobile phone base stations in the Tampere area operate as follows. The area is divided into squares. The squares form an S * S matrix with the rows and columns numbered from 0 to S-1. Each square contains a base station. The number of active mobile phones inside a square can change because a phone is moved from a square to another or a phone is switched on or off. At times, each base station reports the change in the number of active phones to the main base station along with the row and the column of the matrix.
Write a program, which receives these reports and answers queries about the current total number of active mobile phones in any rectangle-shaped area.
Input
The input is read from standard input as integers and the answers to the queries are written to standard output as integers. The input is encoded as follows. Each input comes on a separate line, and consists of one instruction integer and a number of parameter integers according to the following table.
The values will always be in range, so there is no need to check them. In particular, if A is negative, it can be assumed that it will not reduce the square value below zero. The indexing starts at 0, e.g. for a table of size 4 * 4, we have 0 <= X <= 3 and 0 <= Y <= 3.
Table size: 1 * 1 <= S * S <= 1024 * 1024
Cell value V at any time: 0 <= V <= 32767
Update amount: -32768 <= A <= 32767
No of instructions in input: 3 <= U <= 60002
Maximum number of phones in the whole table: M= 2^30
Output
Your program should not answer anything to lines with an instruction other than 2. If the instruction is 2, then your program is expected to answer the query by writing the answer as a single line containing a single integer to standard output.
Sample Input
0 4
1 1 2 3
2 0 0 2 2
1 1 1 2
1 1 2 -1
2 1 1 2 3
3
Sample Output
3
4思路:二维空间单点修改区间查询问题,套模板即可。唯一需要注意的是,本题中的数据,指定的空间为0~S-1,而模板中为了简单使用的是从1开始的区间范围,因此需要将数据做+1的平移。
#include<cstdio>
#include<cstring>
using namespace std;
const int MaxN = 1030;
typedef long long ll;
ll Tree[MaxN][MaxN];
int S;
int lowbit(int x){
return x & (-x);
}
void update(int x,int y,ll delta){
int j;
while(x <= S){
j = y;
while(j <= S){
Tree[x][j] += delta;
j += lowbit(j);
}
x += lowbit(x);
}
}
ll getSum(int x,int y){
ll sum=0;
int j;
while(x){
j = y;
while(j){
sum += Tree[x][j];
j -= lowbit(j);
}
x -= lowbit(x);
}
return sum;
}
int main(){
int ins,X,Y,A,L,B,R,T;
while( scanf("%d",&ins) && ins != 3 ){
switch(ins){
case 0:scanf("%d",&S);
memset(Tree,0,sizeof(Tree));
break;
case 1:scanf("%d",&X);X += 1;
scanf("%d",&Y);Y += 1;
scanf("%d",&A);
update(X,Y,A);
break;
case 2:scanf("%d",&L);L += 1;
scanf("%d",&B);B += 1;
scanf("%d",&R);R += 1;
scanf("%d",&T);T += 1;
printf("%lld\n",getSum(R,T) - getSum(L-1,T) - getSum(R,B-1) + getSum(L-1,B-1));
break;
}
}
} 2.区间修改,单点查询
仿照一维的做法,我们需要在二维上构建差分数组。我们需要明白,当我们把前缀和求和的思想引入差分数组就可以求得原来某个位置的数。因此差分数组的具体生成方式要看前缀和是如何作用的:
通过前面的分析我们知道,在二维下,前缀和有如下关系:
同时我们也得到:
由此我们可以得到二维差分公式:
于是我们只需要再把这个二维差分数组构建成树状数组即可。
当我们需要对[X1,Y1]~[X2,Y2]的矩形区域添加增量delta时,我们需要以[X1,Y1]和[X2+1,Y2+1]为起点,更新增量delta,并以[X1,Y2]和[X2,Y1]为起点,更新增量-delta,做法如下:

#include<bits/stdc++.h>
using namespace std;
int C[1010][1010],A[1010][1010];
int lowbit(int x){
return x&(-x);
}
void update(int x,int y,int n,int m,int delta){
int j;
while(x<=n){
j=y;
while(j<=m){
C[x][j]+=delta;
j+=lowbit(j);
}
x+=lowbit(x);
}
}
void add(int X1,int Y1,int X2,int Y2,int delta,int n,int m){
update(X1,Y1,n,m,delta);
update(X2+1,Y2+1,n,m,delta);
update(X2+1,Y1,n,m,-delta);
update(X1,Y2+1,n,m,-delta);
}
int getSum(int x,int y){
int sum=0,j;
while(x){
j=y;
while(j){
sum+=C[x][j];
j-=lowbit(j);
}
x-=lowbit(x);
}
return sum;
}
int getValue(int X,int Y){
return getSum(X,Y);
}
int main(){
int n,m,i,j,c;
cin>>n>>m;
for(i=1;i<=n;++i){
for(j=1;j<=m;++j){
cin>>A[i][j];
c=A[i][j]-A[i-1][j]-A[i][j-1]+A[i-1][j-1];
update(i,j,n,m,c);
}
}
return 0;
} POJ 2155 Martix
Given an N*N matrix A, whose elements are either 0 or 1. A[i, j] means the number in the i-th row and j-th column. Initially we have A[i, j] = 0 (1 <= i, j <= N).
We can change the matrix in the following way. Given a rectangle whose upper-left corner is (x1, y1) and lower-right corner is (x2, y2), we change all the elements in the rectangle by using "not" operation (if it is a '0' then change it into '1' otherwise change it into '0'). To maintain the information of the matrix, you are asked to write a program to receive and execute two kinds of instructions.
1. C x1 y1 x2 y2 (1 <= x1 <= x2 <= n, 1 <= y1 <= y2 <= n) changes the matrix by using the rectangle whose upper-left corner is (x1, y1) and lower-right corner is (x2, y2).
2. Q x y (1 <= x, y <= n) querys A[x, y].
Input
The first line of the input is an integer X (X <= 10) representing the number of test cases. The following X blocks each represents a test case.
The first line of each block contains two numbers N and T (2 <= N <= 1000, 1 <= T <= 50000) representing the size of the matrix and the number of the instructions. The following T lines each represents an instruction having the format "Q x y" or "C x1 y1 x2 y2", which has been described above.
Output
For each querying output one line, which has an integer representing A[x, y].
There is a blank line between every two continuous test cases.
Sample Input
1
2 10
C 2 1 2 2
Q 2 2
C 2 1 2 1
Q 1 1
C 1 1 2 1
C 1 2 1 2
C 1 1 2 2
Q 1 1
C 1 1 2 1
Q 2 1
Sample Output
1
0
0
1思路:不知道有没有小伙伴和笔者一开始的想法一致。笔者一开始认为只要我们保存A[i][j],当我们翻转它之后,如果它是1,那么翻转前是0,得出delta为1,同理另一个delta为-1。然而这种想法的误区在于,这种想法只适合要翻转的区间内,所有的值都为 0或者都为1时才正确,否则会造成在求和后一些数值是超过2的。然而实际上,我们不需要考虑这么多,或者说,我们应该把所有的偶数全部是为0,把所有的奇数视为1,所以结果需要%2,不管我们是否用了第一个想法,都需要做取余,而第一个想法不做取余的后果是,虽然得到的结果和翻转的结果同奇偶性,但不一定是0和1,可能比他们大得多,比如同样是偶数,由于没有取余,得到的结果是10。
#include<cstdio>
#include<cstring>
using namespace std;
const int MaxN = 1010;
typedef long long ll;
ll Tree[MaxN][MaxN];
int N;
int lowbit(int x){
return x & (-x);
}
void update(int x,int y,ll delta){
int j;
while(x <= N){
j = y;
while(j <= N){
Tree[x][j] += delta;
j += lowbit(j);
}
x += lowbit(x);
}
}
ll getSum(int x,int y){
ll sum=0;
int j;
while(x){
j = y;
while(j){
sum += Tree[x][j];
j -= lowbit(j);
}
x -= lowbit(x);
}
return sum;
}
int main(){
int X, T, x1, y1, x2, y2, delta;
char op;
//cin >> X;
scanf("%d", &X);
while( X -- ){
memset(Tree,0,sizeof(Tree));
//cin >> N >> T;
scanf("%d%d", &N, &T);
while( T -- ){
//cin >> op;
scanf("%c%c", &op,&op);
if( op == 'C'){
//cin >> x1 >> y1 >> x2 >> y2;
scanf("%d%d%d%d", &x1 ,&y1, &x2, &y2);
update(x1, y1, 1);
update(x2+1, y2+1, 1);
update(x1, y2+1, -1);
update(x2+1, y1, -1);
}else{
//cin >> x1 >> y1;
scanf("%d%d", &x1, &y1);
//cout << getSum(x1 , y1)<<endl;
printf("%lld\n",getSum(x1,y1)%2);
}
}
if( X )printf("\n");
}
} 修改后的想法一:
#include<cstdio>
#include<cstring>
using namespace std;
const int MaxN = 1010;
typedef long long ll;
ll Tree[MaxN][MaxN],A[MaxN][MaxN];
int N;
int lowbit(int x){
return x & (-x);
}
void update(int x,int y,ll delta){
int j;
while(x <= N){
j = y;
while(j <= N){
Tree[x][j] += delta;
j += lowbit(j);
}
x += lowbit(x);
}
}
ll getSum(int x,int y){
ll sum=0;
int j;
while(x){
j = y;
while(j){
sum += Tree[x][j];
j -= lowbit(j);
}
x -= lowbit(x);
}
return sum;
}
int main(){
int X, T, x1, y1, x2, y2, delta;
char op;
//cin >> X;
scanf("%d", &X);
while( X -- ){
memset(A,0,sizeof(A));
memset(Tree,0,sizeof(Tree));
//cin >> N >> T;
scanf("%d%d", &N, &T);
while( T -- ){
//cin >> op;
scanf("%c%c", &op,&op);
if( op == 'C'){
//cin >> x1 >> y1 >> x2 >> y2;
scanf("%d%d%d%d", &x1 ,&y1, &x2, &y2);
A[x1][y1] ^= 1;
delta = A[x1][y1] == 0 ? -1 : 1;
update(x1, y1, delta);
update(x2+1, y2+1, delta);
update(x1, y2+1, -delta);
update(x2+1, y1, -delta);
}else{
//cin >> x1 >> y1;
scanf("%d%d", &x1, &y1);
//cout << getSum(x1 , y1)<<endl;
printf("%lld\n",getSum(x1,y1)%2);
}
}
if( X )printf("\n");
}
} 3.区间修改,区间查询
在二维差分数组中,[1,1]~[x,y]的有效信息和可以用如下式表示
右边的式子可以这么理解,前两个求和是在枚举x*y个点,后两个求和是在针对每一个点,用二维差分数组求值。依旧仿照一维的方式,将式子打开,统计每个差分值出现的次数,我们可以知道,对于点(i,j),在计算[1,1]~[x,y]时出现的次数为(x+1-i)*(y+1-j)。【换种思路也可以这么想,差分值C[i][j]只有在k>=i&&h>=j时才会被累积到】。于是我们有下式:
不要忘了我们在一维中提到过,对于x,y这种量是会随着我们统计的区间改变的,因此我们必须消去它或者不让它和i,j这两个枚举变量纠缠在一次,我们尝试打开这个式子得到:
于是我们将x,y与i,j分离,此时只需要维护四个数组C[i][j],C[i][j]*i,C[i][j]*j,C[i][j]*i*j。不要忘了,后三个数组都是为了辅助D[i][j]存在的,因此他们的更新规则要依赖于D[i][j]。
#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int C1[N][N],C2[N][N],C3[N][N],C4[N][N],A[N][N];// C2[i][j]=C1[i][j]*i C3[i][j]=C1[i][j]*j C4[i][j]=C1[i][j]*i*j
int lowbit(int x){
return x&(-x);
}
void update(int C[N][N],int x,int y,int n,int m,int delta){
int j;
while(x<=n){
j=y;
while(j<=m){
C[x][j]+=delta;
j+=lowbit(j);
}
x+=lowbit(x);
}
}
int getSum(int C[N][N],int x,int y){
int sum=0,j;
while(x){
j=y;
while(j){
sum+=C[x][j];
j-=lowbit(j);
}
x-=lowbit(x);
}
return sum;
}
void RectUpdate(int X1,int Y1,int X2,int Y2,int n,int m,int delta){///区间更新
//差分数组C1更新
update(C1,X1,Y1,n,m,delta);
update(C1,X2+1,Y2+1,n,m,delta);
update(C1,X1,Y2+1,n,m,-delta);
update(C1,X2+1,Y1,n,m,-delta);
//C2更新 C2[i][j]=i*C1[i][j]
update(C2,X1,Y1,n,m,X1*delta);
update(C2,X2+1,Y2+1,n,m,(X2+1)*delta);
update(C2,X1,Y2+1,n,m,(X1)*(-delta));
update(C2,X2+1,Y1,n,m,(X2+1)*(-delta));
//C3更新 C3[i][j]=j*C1[i][j]
update(C3,X1,Y1,n,m,Y1*delta);
update(C3,X2+1,Y2+1,n,m,(Y2+1)*delta);
update(C3,X1,Y2+1,n,m,(Y2+1)*(-delta));
update(C3,X2+1,Y1,n,m,Y1*(-delta));
//C4更新 C4[i][j]=i*j*C1[i][j]
update(C4,X1,Y1,n,m,Y1*Y1*delta);
update(C4,X2+1,Y2+1,n,m,(X2+1)*(Y2+1)*delta);
update(C4,X1,Y2+1,n,m,X1*(Y2+1)*(-delta));
update(C4,X2+1,Y1,n,m,(X2+1)*Y1*(-delta));
}
int RectSum(int X1,int X2,int Y1,int Y2){
int L = (X1-1+1)*(Y1-1+1)*getSum(C1,X1-1,Y1-1)-(Y1-1+1)*getSum(C2,X1-1,Y1-1)-(X1-1+1)*getSum(C3,X1-1,Y1-1)+getSum(C4,X1-1,Y1-1);
int R = (X2+1)*(Y2+1)*getSum(C1,X2,Y2)-(Y2+1)*getSum(C2,X2,Y2)-(X2+1)*getSum(C3,X2,Y2)+getSum(C4,X2,Y2);
return R-L;
}
int main(){
int n,m,i,j,c;
cin>>n>>m;
for(i=1;i<=n;++i){
for(j=1;j<=m;++j){
cin>>A[i][j];
c=A[i][j]-A[i-1][j]-A[i][j-1]+A[i-1][j-1];
update(C1,i,j,n,m,c);//差分数组生成
update(C2,i,j,n,m,i*c);
update(C3,i,j,n,m,j*c);
update(C4,i,j,n,m,i*j*c);
}
}
return 0;
} 目前没碰到相关题目,以后遇到了补上。=m=






















 779
779











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








