机器学习-线性模型

线性模型是机器学习中最基础的模型，在中学学过的最小二乘法其实就是机器学习中的一种线性模型。我们先来回忆一下最小二乘法是什么

最小二乘法与基本线性回归

假设有如下所示的5个数据

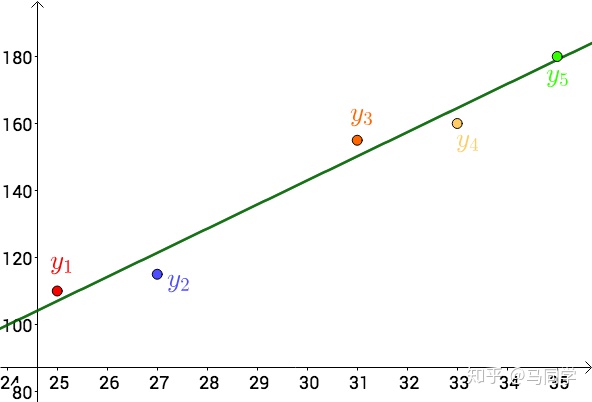
似乎这5个数据是在这条绿线上下浮动，我们的目的就是找到这条绿线的函数表达式。我们先假设这条绿线的函数表达式是
$$\hat{y}=ax+b$$
现在我们的问题就转换成了找到$a$和$b$的值。我们希望数据点尽可能多地落在函数图像上，即数据的误差和拟合直线的误差越小越好。由此得到以下式子
$$(a,b)=argmin\sum _{i=1}^5|y_i-\hat{y}|$$
其中${\sum }_{i=1}^5|y_i-\hat{y}|$被称为代价函数（cost function）

由于计算机处理绝对值很麻烦，我们常常将这类问题转换成
$$(a,b)=argmin\sum _{i=1}^5(y_i-\hat{y}{)}^2$$
在中学阶段，我们通过猜测来推断出$a$和$b$的值，而到了大学阶段，我们很容易地看出这是一个二元函数求极值的问题。

在机器学习中，我们遇到的问题常常有多个维度，于是我们要拟合的函数表达式就变成了
$$f(x)=w_1{x}_1+w_2{x}_2+...w_d{x}_d+b$$
写成向量形式
$$f(x)=w^{T}x+b$$
*注意：之后的式子若无特别说明均为向量形式

为了方便，我们把$b$和$w$写成一个向量
$$\hat{w}=(w;b)$$
相应的，在$x$最后一列恒置1（$b$被吸收后空出的）
$$X=\left[\begin{array}{ccccc}{x}_{11}& x_{12}& \cdots & x_{1d}& 1\\ x_{21}& x_{22}& \cdots & x_{2d}& 1\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ x_{m1}& x_{m2}& \cdots & x_{md}& 1\end{array}\right]$$
于是整个式子就变成了
$$f(x)=X\hat{w}$$
根据上面最小二乘法的思路，我们的问题也就转换成了
$${\hat{w}}^{\ast }=\underset{\hat{w}}{\mathrm{argmin}}(y-X\hat{w}{)}^2$$
在线性代数中，矩阵的平方常常表示成该矩阵的转置与其相乘的形式，于是$(9)$式就变成了
$${\hat{w}}^{\ast }=\underset{\hat{w}}{\mathrm{argmin}}(y-X\hat{w}{)}^T(y-X\hat{w})$$
按照常规思路，令$\hat{w}=(y-X\hat{w}{)}^T(y-X\hat{w})$，对$\hat{w}$进行求导得
$$\frac{\partial \hat{w}}{\partial \hat{w}}=2(X\hat{w}-y)X$$
与西瓜书上不同是因为书上采用的是分母布局，本质是一个式子。将上式等于0，求解${\hat{w}}^{\ast }$带入$(8)$式，即可得出结果

在$X^{T}X$为满佚矩阵时
$${\hat{w}}^{\ast }=(X^{T}X{)}^{-1}{X}^{T}y$$

对数几率回归（logistic回归）

对于一个线性回归问题，上面的方法可以很好地解决。但是对于分类问题，一个直线就很难拟合数据的分布特点，下面我们以二分类问题为例，研究logistics回归。

对于一个二分类问题，最好的拟合函数是“单位阶跃函数”
$$y=\{\begin{array}{cc}0,& z<0;\\ 0.5,& z=0;\\ 1,& z>0\end{array}$$
但是这个函数不可导，难以以最小二乘法的思想求拟合曲线，我们可以另选一个函数。希望$z<0$时函数尽量为0，$z>0$时函数尽量为1。sigmoid函数就是这么一个函数
$$y=\frac{1}{1+e^{-z}}$$
图像如下

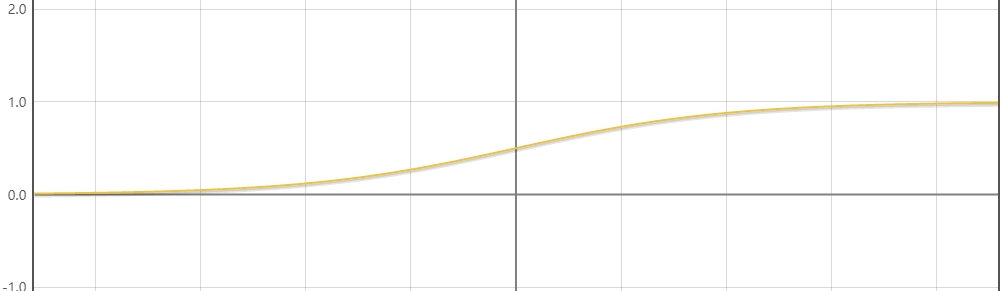
现在看来这个图像并不好，但当我们把$z$之前的系数变成-100的时候图像如下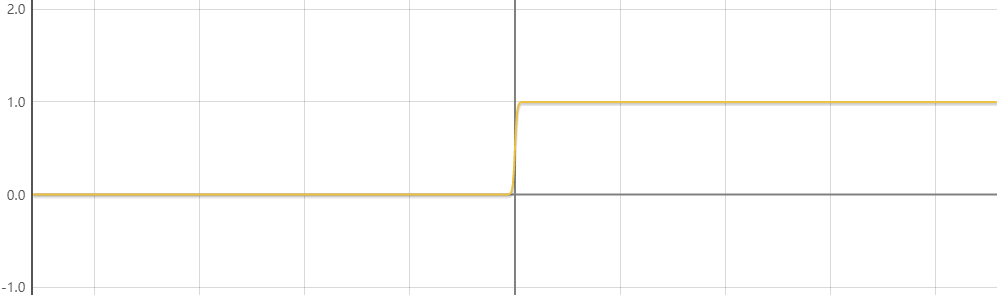

这样看来图像就像是我们所需要的样子了。事实上$z$完全可以作为一个隐函数，这样我们的目标就变成了找到一个合适的函数$z$，就可以使用上面最小二乘法的思路了。根据上面的思路，式$(14)$变成了
$$y=\frac{1}{1+e^{-(w^{T}x+b)}}$$
如果我们在按照上面的思路MSE（均方误差，mean square error），由于加了一个sigmoid函数，使得整个函数变成非凸函数，可能有多个导数为0的点，很容易落入局部最优中。我们可以从概率的角度来推导logistic回归的代价函数。（说实话，我挺不喜欢这种方法的，但是我又不会其他方法ヽ(ー_ー)ノ）

设
$$P(y=0|x)=\frac{1}{1+e^{-(w^{T}x+b)}}$$
相应的
$$P(y|x)=\{\begin{array}{cc}\frac{1}{1+e^{-（w^{T}x+b）}},& y=0\\ \frac{e^{-（w^{T}x+b）}}{1+e^{-（w^{T}x+b）}},& y=1\end{array}$$
将上式融合为一个式子
$$P(y_i|x_i)=p^{y_i}(1-p{)}^{(1-y_i)}$$
其中
$$p=\frac{e^{w^{T}x+b}}{1+e^{w^{T}x+b}}$$
根据最大似然估计，最大似然函数为
$$P(y_i|x_i;w,b)=\prod _{i=1}^m{p}^{y_i}(1-p{)}^{(1-y_i)}=\sum _{i=1}^m\ln p^{y_i}(1-p{)}^{(1-y_i)}=\sum _{n=1}^N\left(y_n\ln (p)+\left(1-y_n\right)\ln (1-p)\right)$$
由于代价函数一般是求最小值，所以需要在上面式子中添加一个负号，最终的式子为
$$(w^{\ast },b^{\ast })=\underset{w,b}{\mathrm{argmin}}\left\{-\sum _{n=1}^N\left(y_n\ln (p)+\left(1-y_n\right)\ln (1-p)\right)\right\}$$
使用梯度下降法或牛顿法即可求得最优解。

线性判别分析

线性判别分析（LDA，linear discriminant analysis）和降维中的PCA非常像。LDA的基本思想是给定训练集，将这样样例投影到一个直线上，使相同样例的投影尽可能近，不同样例的投影点尽可能远离，其实就是“高内聚，低耦合”的思想。

我们假设直线$w$，且$||w||=1$，给定数据集 D = ( x i , y i ) i = 1 m , y i ∈ { 0 , 1 } D={(x_i,y_i)}^m_{i=1},y_i∈\{0,1\} D=(xi​,yi​)i=1m​,yi​∈{0,1}，易知数据在$w$上的投影为$w^T{x}_i$，${\bar{z}}_{y_i}$为投影的均值，即
$${\bar{z}}_{y_i}=\frac{1}{N_i}\sum _{i=1}^{N_i}{w}^T{x}_i$$
设${\mu }_i$为数据的均值向量，即
$${\mu }_i=\frac{1}{N_i}\sum _{i=1}^{N_i}{x}_i$$
设$S_{y_i}$为投影方差，即
$$S_{y_i}=\frac{1}{N_i}\sum _{i=1}^{N_i}(w^T{x}_i-{\bar{z}}_i)(w^T{x}_i-{\bar{z}}_i{)}^T$$
其实$S_i$是个标量，我这么写其实是为了方便看。根据LDA的基本思想，我们便很容易的找到了目标函数。
$$J=\frac{({\bar{z}}_1-{\bar{z}}_2{)}^2}{S_1+S_2}$$
我们的目标就是找到一个$w$使分子尽量大，分母尽量小，即函数$J$取得最大值，即
$$w^{\ast }=argmax\frac{({\bar{z}}_1-{\bar{z}}_2{)}^2}{S_1+S_2}$$

设类间散度矩阵
$$S_b=({\mu }_1-{\mu }_2)({\mu }_1-{\mu }_2{)}^T$$

设类内方差矩阵
$$S_{c1}=\frac{1}{N_1}\sum _{i=1}^{N_1}\left[\left(x_i-{\mu }_1\right){\left(x_i-{\mu }_1\right)}^T\right]$$

$$S_{c2}=\frac{1}{N_2}\sum _{i=1}^{N_2}\left[\left(x_i-{\mu }_2\right){\left(x_i-{\mu }_2\right)}^T\right]$$

首先看分子
$$\begin{gathered} ({\bar{z}}_1-{\bar{z}}_2{)}^2=(\frac{1}{N_1}\sum _{i=1}^{N_1}{w}^T{x}_1-\frac{1}{N_2}\sum _{i=1}^{N_2}{w}^T{x}_2{)}^2=(w^T({\mu }_1-{\mu }_2){)}^2=w^T({\mu }_1-{\mu }_2)({\mu }_1-{\mu }_2{)}^{T}w \\ =w^T{S}_{b}w \end{gathered}$$
在看分母
$$\begin{gathered} S_1+S_2=\frac{1}{N_1}\sum _{i=1}^{N_1}(w^T{x}_i-{\bar{z}}_1)(w^T{x}_i-{\bar{z}}_1{)}^T+\frac{1}{N_2}\sum _{i=1}^{N_2}(w^T{x}_i-{\bar{z}}_2)(w^T{x}_i-{\bar{z}}_2{)}^T \\ =\frac{1}{N_1}\sum _{i=1}^{N_1}(w^T{x}_i-\frac{1}{N_1}\sum _{i=1}^{N_1}{w}^T{x}_i)(w^T{x}_i-\frac{1}{N_1}\sum _{i=1}^{N_1}{w}^T{x}_i{)}^T+\frac{1}{N_2}\sum _{i=1}^{N_2}(w^T{x}_i-\frac{1}{N_2}\sum _{i=1}^{N_2}{w}^T{x}_i)(w^T{x}_i-\frac{1}{N_2}\sum _{i=1}^{N_2}{w}^T{x}_i{)}^T \\ =w^T\frac{1}{N_1}\sum _{i=1}^{N_1}\left[\left(x_i-{\mu }_1\right){\left(x_i-{\mu }_1\right)}^T\right]w+w^T\frac{1}{N_2}\sum _{i=1}^{N_2}\left[\left(x_i-{\mu }_2\right){\left(x_i-{\mu }_2\right)}^T\right]w \\ =w^T(S_{c1}+S_{c2})w \end{gathered}$$
令
$$S_w=S_{c1}+S_{c2}$$

由以上式子可得
$$J=\frac{w^T{S}_{b}w}{w^T{S}_{w}w}$$
对上式求导，并令导数为0
$$\begin{array}{rl}\frac{\partial J(w)}{\partial w}=2S_{b}w\cdot {\left(w^T{S}_{w}w\right)}^{-1}+\left(w^T{S}_{b}w\right)\cdot (-1){\left(w^T{S}_{w}w\right)}^{-2}\cdot 2S_{w}w& =0\\ S_{b}w-\left(w^T{S}_{b}w\right)\cdot {\left(w^T{S}_{w}w\right)}^{-1}\cdot S_{w}w& =0\\ S_{b}w& =\frac{w^T{S}_{b}w}{w^T{S}_{w}w}{S}_{w}w\\ w& =\frac{w^T{S}_{w}w}{w^T{S}_{b}w}{S}_w^{-1}{S}_{b}w\end{array}$$
其中，易知$\frac{w^T{S}_{w}w}{w^T{S}_{b}w}$为标量，$S_{b}w=({\mu }_1-{\mu }_2)({\mu }_1-{\mu }_2{)}^{T}w$中的$({\mu }_1-{\mu }_2{)}^{T}w$也是标量，所以可以得出
$$w\propto S_w^{-1}({\mu }_1-{\mu }_2)$$
由于我们要求的是一个直线，所以不必在乎结果的大小，而只要关注方向即可，所以$S_w^{-1}({\mu }_1-{\mu }_2)$的方向即我们所要求的直线的方向。

改LaTeX的代码真是酸爽┭┮﹏┭┮

多分类学习

多分类学习的基本思想是把多分类任务拆解成多个二分类任务，拆解方法有“一对一”（OvO），“一对其余”（OvR），“多对多”（MvM）

OvO将数据集中的所有数据两两配对，产生$N(N-1)/2$个分类任务，为每一个任务训练一个分类器，测试时将测试样本提交给所有分类器，由所有分类器投票，票数最多的类别作为最终分类结果。

OvR将一个类别作为正例，其余类别作为反例训练分类器，由此产生$N$个分类器，测试时将测试样本提交给所有分类器，结果为正的则作为最终分类结果，若有过个分类器结果均为正，则选择分类器置信度最大的那个作为最终分类结果。

MvM是将若干类作为正类，其他类作为反类。其中最常用的是“纠错输出码”（error correcting output codes，ECOC）。

编码阶段：对$N$个类别做$M$次划分，每次划分将一部分化为正类，另一部分为反类。可以训练除M个分类器。

解码阶段：将测试样本提交给所有分类器，将分类器返回的结果组成编码，与每个类别各自的编码进行比较，其中距离（汉明距离或欧氏距离）最小的类别最为最终分类结果。

书上还有一个类别不平衡问题，其实就是个加权，没什么数学推导，我认为没必要写。