【算法】【算法杂谈】判断点是否在三角形内部（面积法和向量法）

最新推荐文章于 2025-01-07 21:32:42 发布

原创

最新推荐文章于 2025-01-07 21:32:42 发布 · 3.6k 阅读

23 ·

CC 4.0 BY-SA版权

文章标签：

#算法

文章介绍了两种方法来判断一个点是否位于三角形内部，包括使用面积法（基于海伦公式）和向量法。面积法简洁但可能因精度问题导致误判，而向量法则更为精确。文章提供了Java代码示例，并提到C和C++版本正在学习中。

前言

当前所有算法都使用测试用例运行过，但是不保证100%的测试用例，如果存在问题务必联系批评指正~

在此感谢左大神让我对算法有了新的感悟认识！

问题介绍

原问题
给定三个点坐标代表三角形的三个顶点，再给定一个（x,y）点，判断该点是否在三角形内部

解决方案

原问题：
方法一：面积法
1、利用海伦公式求出以改点为顶点，三角形各边为底边的三角形面积之和，如果该和大于三角形的总面积，那么点在外面，如果不大于，则点在里面
优点：容易想到，容易编写，只需要编写点到点之间的距离即可利用公式快速计算面积从而判断答案
缺点：由于海伦公式存在开根会导致精度缺失判断失误
方法二：向量法
如下图：
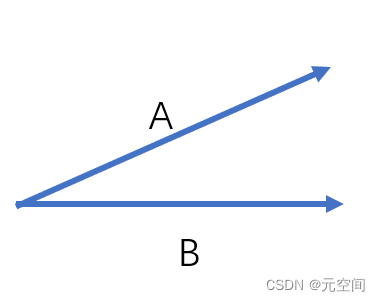
在这里插入图片描述
1、向量的叉乘，假设A(2,1) B(2,0)，则AxB = 0-2 = -2 < 0 ,也就是说如果A向量旋转到B向量同向时，叉乘为负数，反之则为正数
2、由此可以得到一个点在向量的那一侧，如果在右侧，那么叉乘为负数，如果在左侧，那么叉乘为正数
3、为什么要这个准备工作呢？我们再看一张图：
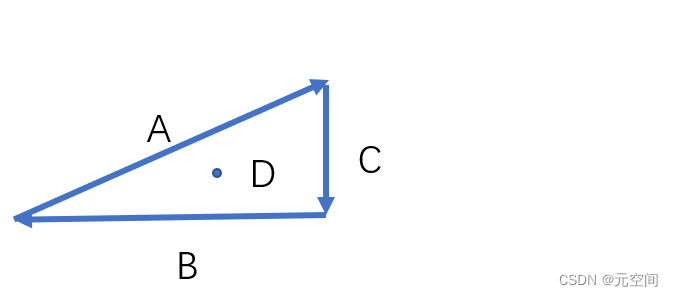
在这里插入图片描述

4、如果D点在三角形内，那么我们就能够得到D点一定在ABC三条边的同一侧！
5、所以更具这个定理我们只需要写一个叉乘的方法就能够解决
优点：简单快捷、没有精度缺失问题
缺点：不容易想到，容易被方法一抢风头~

代码编写

java语言版本

原问题：
方法一:

   /**
     * 二轮测试：判断点是否在三角形的内部
     * 方法一：面积法
     * @param x1
     * @param y1
     * @param x2
     * @param y2
     * @param x3
     * @param y3
     * @param x
     * @param y
     * @return
     */
    public static boolean isInsideCp1(double x1, double y1,
                                      double x2, double y2,
                                      double x3, double y3,
                                      double x, double y) {
   
   
        return getSquare(x1, y1, x2, y2, x, y) + getSquare(x1, y1, x3, y3, x, y) + getSquare(x3, y3, x2, y2, x, y)
                <= getSquare