版权声明:本文为博主原创文章,未经博主允许不得转载。
LinkedList,从字面上明显可以看出它是一个基于链表的list。通常来说,我们也只把它当做一个ArrayList的替代品,因为它具备插入删除快,对存储要求低等优点。但是看过源码之后,你会发现它着实是个多面手。
LinkedList类定义:
public class LinkedList<E> extends AbstractSequentialList<E>
implements List<E>, Deque<E>, Cloneable, java.io.Serializable
- 1
- 2
从类定义可以看出,LinkedList其实不止实现了List接口,Cloneable, Serializable这两个常规接口,此外还实现了Deque接口。正是如此,它不仅仅是个列表(List),同时还是个双向队列(Deque),栈(Stack)。接下来,本文将简单介绍LinkedList的基础数据结构,并通过实践叙述它的三大功能。
数据结构
现在,从基础数据结构说起。LinkedList由一个个Node组成,每个Node包括一个数据元素和两个分别纸箱前后结点的指针。Node的数据结构定义为:
private static class Node<E> {
E item; //存储结点数据,允许为空
Node<E> next;
Node<E> prev;
Node(Node<E> prev, E element, Node<E> next) {
this.item = element;
this.next = next;
this.prev = prev;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
一个链表结构为:

当删除第三个结点,链表结构变为:

在Node4和Node5之间插入一个结点,链表结构变为:
做个本分的List
作为一个list,它实现了基类List的所有方法,诸如add,remove,contains,get,set,size等。接下来我们简单实践几个简单的方法。
public class LinkedListGo {
public static void main(String[] args) {
List<String> list = new LinkedList<String>(Arrays.asList(new String[]{"HashMap", "TreeMap", "LinkedHashMap"}));
//使用addAll批量添加
list.addAll(Arrays.asList(new String[]{"ArrayList", "LinkedList", "Vector"}));
list.add("ConcurrentLinkedDeque");
list.add("Collections");
//使用size()方法获取list中元素个数
System.out.println("Size of this list is : " + list.size() + "\n");
//使用get(),set()方法获取和设置list中元素的值
System.out.println("The sixth element of the list is : " + list.get(6));
list.set(6, "ConcurrentHashMap");
System.out.println("After setting, the sixth element of the list is : " + list.get(6) + "\n");
//使用contains()判断列表是否包号某个元素,remove()删除元素
System.out.println("This lis contains \"Collections\": " + list.contains("Collections"));
list.remove("Collections");
System.out.println("After removing \"Collection\", this lis contains \"Collections\": " + list.contains("Collections") + "\n");
//使用toArray转化为数组,使用removeAll批量删除
String[] strs = list.toArray(new String[]{});
list.removeAll(new LinkedList<String>(Arrays.asList(strs)));
System.out.println("After removing all, currently, the list is empty: " + list.isEmpty());
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
关于LinkedList的几点说明
1. 以上代码中为LinkedList赋值时,语句中之所以要使用new LinkedList(...),看似多次一举,实则是处于安全考虑,集体请参考Java程序员常犯的十个错误;
2. 不同于ArrayList,但凡是涉及到元素index的操作,LinkedList不是直接根据index对元素进行操作,而是先遍历找到index对应元素,然后进行操作;
Queue:创建和遍历二叉树
现在我们要构建一棵二叉树,如下图所示:
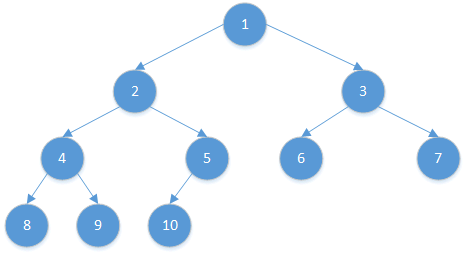
首先定义二叉树结点:
public class TreeNode<E> {
public E data; //数据结点
public TreeNode<E> left; //指向左子树
public TreeNode<E> right; //指向右子树
public TreeNode() {
}
public TreeNode(E data, TreeNode<E> left, TreeNode<E> right) {
this.data = data;
this.left = left;
this.right = right;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
然后定义一棵二叉树,代码如下:
public class BinaryTree<E> {
private TreeNode<E> root; //定义树根节点
public BinaryTree() {
}
public BinaryTree(TreeNode<E> root) {
super();
this.root = root;
}
public BinaryTree(E[] elements) {
super();
buildTree(elements); //构建二叉树,方法见下文
}
...//二叉树相关方法
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
接下来我们通过队列构建二叉树,构建方法的参数为结点元素数组,代码如下:
public void buildTree(E[] elements) {
if (elements == null || elements.length == 0)
return;
//二叉树结点队列
Deque<TreeNode<E>> queue = new LinkedList<TreeNode<E>>();
TreeNode<E> node = new TreeNode<E>();
this.root = node;
for (E element : elements) {
node.data = element;
node.left = new TreeNode<E>();
node.right = new TreeNode<E>();
//将左右两个新创建结点加入队列
queue.offer(node.left);
queue.offer(node.right);
//创建完一个结点之后,从队列中取出一个结点接续操作
node = queue.poll();
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
接下来,我们同样可以使用队列实现对这棵二叉树的广度优先遍历,实现方法简单思路如下:
- 从根结点开始,将结点入队;
- 如果队列不为空,则从队列中取出一个结点,然后将此结点的左子树和右子树(如果存在)入队;
- 循环第2步,直到队列为空,整棵树的广度优先遍历结束。
代码如下:
public void breadthFirstTraverse() {
Deque<TreeNode<E>> queue = new LinkedList<TreeNode<E>>();
TreeNode<E> node = this.root;
queue.offer(node);
while (!queue.isEmpty()) {
node = queue.poll();
if (node.data != null) {
System.out.print(node.data + "\t");
}
if(node.left != null) {
queue.offer(node.left);
}
if(node.right != null) {
queue.offer(node.right);
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
实验代码:
public static void main(String[] args) {
BinaryTree<String> tree = new BinaryTree<String>(new String[] { "1",
"2", "3", "4", "5", "6", "7", "8",
"9", "10" });
System.out.println("\n======Breadth-First Traverse======");
tree.breadthFirstTraverse();
- 1
- 2
- 3
- 4
- 5
- 6
运行结果:
Stack:先序,中序,后序非递归遍历二叉树
二叉树的先序,中序和后续遍历是二叉树的最基本操作。因为二叉树和它的二叉子树具有结构相同的特征,因此,最通用的方法就是递归遍历。换个角度来看,三种遍历方法都可视为深度(DFS)优先遍历。既是深度优先遍历,那么我们首先联想到的便是使用栈实现。接下来我们将通过非递归遍历二叉树来实践LinkedList作为栈的功能。
非递归先序遍历
public void preOrderTraverse() {
if (root == null) {
return;
}
//使用LinkedList作为二叉树遍历的栈
Deque<TreeNode<E>> stack = new LinkedList<TreeNode<E>>();
TreeNode<E> node = root;
stack.push(node);
while (!stack.isEmpty()) {
node = stack.pop();//pop弹出栈最上方结点
if (node.data != null) {
System.out.print(node.data + "\t");
}
if (node.right != null) {
stack.push(node.right);//将右结点压栈
}
if (node.left != null) {
stack.push(node.left);//将左结点压栈
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
先序遍历较为简单,对于每个遍历到的结点,首先将其右结点压栈,再将其左结点压栈。然后每次从栈顶pop出一个结点,循环往复操作,直到栈中没有结点为止。
非递归中序遍历
public void inOrderTraverse() {
if (root == null) {
return;
}
//声明遍历使用的栈;
Deque<TreeNode<E>> stack = new LinkedList<TreeNode<E>>();
TreeNode<E> node = this.root;
while (node != null || !stack.isEmpty()) {
if (node != null) {
stack.push(node);
node = node.left;
}
else if (!stack.isEmpty()) {
node = stack.pop();
if (node.data != null) {
System.out.print(node.data + "\t");
}
node = node.right;
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
中序遍历稍微有点绕脑筋,大家可以自行根据以上代码,画画入栈出栈图。
非递归后续遍历
public void postOrderTraverse() {
//遍历栈,用于遍历二叉树
Deque<TreeNode<E>> stack = new LinkedList<TreeNode<E>>();
//输出栈,将遍历结果存入此栈,最后一次性出栈输出
Deque<TreeNode<E>> output = new LinkedList<TreeNode<E>>();
TreeNode<E> node = this.root;
stack.push(node);
while (!stack.isEmpty()) {
node = stack.pop();
output.push(node);
if (node.left != null) {
stack.push(node.left);
}
if (node.right != null) {
stack.push(node.right);
}
}
while (!output.isEmpty()) {
TreeNode<E> out = output.pop();
if (out.data != null) {
System.out.print(out.data + "\t");
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
此处后续遍历的实现较为巧妙,我们用了两个栈进行遍历,第一个栈是个临时栈,遍历所有的结点;每当从临时栈中取出结点,将此结点压入输出栈,当遍历结束之后,一次性全部pop出输出栈中结点,即为后续遍历。
遍历结果如下:
LinkedList vs ArrayList
此处,我们将LinkedList和ArrayList进行比较,总结出它的优缺点。
| 优点 | 缺点 |
|---|---|
| 基于链表,一种动态数据结构,可以运行时进行动态扩展和收缩 | 随机访问相较于ArrayList更慢 |
| 插入和删除操作更简单,无需移动元素 | Java8中,没有添加诸如ArrayList中的新方法 |
| 具备更高效的内存利用率,无需预分配内存(即需要多少,占用多少) | |
| 更好地实现栈和队列功能,功能更丰富 |
总结
本文首先简单介绍了LinkedList的基本数据结构,然后通过举例说明了LinkedList作为列表,队列和栈的基本功能;最后和ArrayList进行比较,点明它的优缺点。
文中代码可点击此处下载:LinkedList实践代码
-
顶
- 0
-
踩
- 0













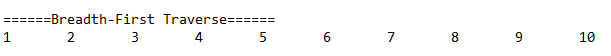
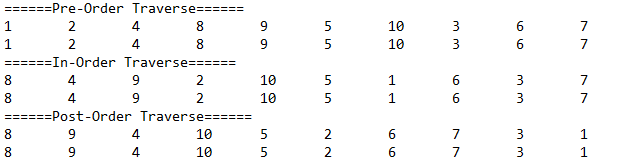














 5231
5231

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








