聚类分析与k均值聚类算法
督学习算法。在给定样本的情况下,聚类分析通过度量特征相似度或者距离,将样本自动划分为若干类别。
距离度量和相似度度量方式
距离度量和相似度度量是聚类分析的核心概念,大多数聚类算法建立在距离度量之上。常用的距离度量方式包括闵氏距离和马氏距离,常用的相似度度量方式包括相关系数和夹角余弦等。
相关系数。
相关系数(correlation coefficent)是度量样本相似度最常用的方式。相关系数越接近1,表示两个样本越相似;相关系数越接近0,表示两个样本越不相似。

夹角余弦。
夹角余弦(angle cosine)也是度量两个样本相似度的方式。夹角余弦越接近1,表示两个样本越相似;夹角余弦越接近0,表示两个样本越不相似。
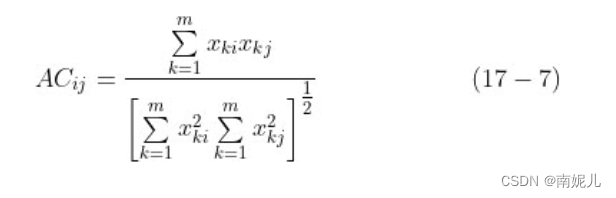
聚类算法
聚类算法通过距离度量将相似的样本归入同一个簇(cluster)中,这使得同一个簇中的样本对象的相似度尽可能大,同时不同簇中的样本对象的差异性也尽可能大
常用的聚类算法有如下几种:
- 基于距离的聚类,该类算法的目标是使簇内距离小、簇间距离大
- 基于密度的聚类,该类算法是根据样本邻近区域的密度来进行划分的,最常见的密度聚类算法当数DBSCAN算法
- 层次聚类算法,包括合并层次聚类和分裂层次聚类等;
- 基于图论的谱聚类算法等。
k均值聚类算法

k均值聚类算法是基于欧式距离进行聚类的算法。
- 首先初始化k个质心,在m个样本中随机选择k个样本作为样本中心。
- 按照样本到k个质心的距离进行聚类。计算每个样本到质心的距离,将其分配到最近的质心所在的类,构成初步的聚类结果
- 将上述聚类的结果,重新计算中新的质心。对每个类求均值,并作为新的质心。
- 如果迭代收敛,或满足条件则停止,否则继续第2步

numpy代码实现
import numpy as np
# 定义欧式距离
def euclidean_distance(x1, x2):
distance = 0
# 距离的平方项再开根号
for i in range(len(x1)):
distance += pow((x1[i] - x2[i]), 2)
return np.sqrt(distance)
# 定义中心初始化函数
def centroids_init(k, X):
m, n = X.shape
centroids = np.zeros((k, n))
for i in range(k):
# 每一次循环随机选择一个类别中心
centroid = X[np.random.choice(range(m))]
centroids[i] = centroid
return centroids
# 定义样本的最近质心点所属的类别索引
def closest_centroid(sample, centroids):
closest_i = 0
closest_dist = float('inf')
for i, centroid in enumerate(centroids): ##遍历每个质心,比较样本距离哪一个质心比较近
# 根据欧式距离判断,选择最小距离的中心点所属类别
distance = euclidean_distance(sample, centroid)
if distance < closest_dist:
closest_i = i
closest_dist = distance
return closest_i
# 定义构建类别过程
def build_clusters(centroids, k, X):
#列表,保存每个类别所有的样本点
clusters = [[] for _ in range(k)]
for x_i, x in enumerate(X): #遍历每个样本,比较每个样本距离哪一个质心最近
# 将样本划分到最近的类别区域
centroid_i = closest_centroid(x, centroids)
clusters[centroid_i].append(x_i)
return clusters
# 根据上一步聚类结果计算新的中心点
def calculate_centroids(clusters, k, X):
n = X.shape[1]
centroids = np.zeros((k, n))
# 以当前每个类样本的均值为新的中心点
for i, cluster in enumerate(clusters):
centroid = np.mean(X[cluster], axis=0)
centroids[i] = centroid
return centroids
# 获取每个样本所属的聚类类别
def get_cluster_labels(clusters, X):
y_pred = np.zeros(X.shape[0])
for cluster_i, cluster in enumerate(clusters):
for X_i in cluster:
y_pred[X_i] = cluster_i
return y_pred
X = np.array([[0,2],[0,0],[1,0],[5,0],[5,2]])
print('两个样本的距离',euclidean_distance(X[0], X[4]))
# 根据上述各流程定义kmeans算法流程
def kmeans(X, k, max_iterations):
# 1.初始化中心点
centroids = centroids_init(k, X)
# 遍历迭代求解
for _ in range(max_iterations):
# 2.根据当前中心点进行聚类
clusters = build_clusters(centroids, k, X)
# 保存当前中心点
prev_centroids = centroids
# 3.根据聚类结果计算新的中心点
centroids = calculate_centroids(clusters, k, X)
# 4.设定收敛条件为中心点是否发生变化
diff = centroids - prev_centroids
if not diff.any():
break
# 返回最终的聚类标签
return get_cluster_labels(clusters, X)
# 设定聚类类别为2个,最大迭代次数为10次
labels = kmeans(X, 2, 10)
# 打印每个样本所属的类别标签
print(labels)sklearn代码实现
import numpy as np
# 测试数据
# X = np.array([[0,2],[0,0],[1,0],[5,0],[5,2]])
X=np.random.randn(100,4)
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=2, random_state=0).fit(X)
# print(kmeans.labels_)
print('预测结果',kmeans.predict([[0, 0,1,1], [1,1,12, 3]]))
print('质心坐标',kmeans.cluster_centers_)主成分分析
主成分分析(principal component analysis,PCA)是一种经典的降维算法。PCA通过正交变换将一组由线性相关变量表示的数据转换为几个由线性无关变量表示的数据,这几个线性无关变量就是主成分。
原理推导
首先将需要降维的数据的各个变量标准化(规范化)为均值为0、方差为1的数据集,然后对标准化后的数据进行正交变换,将原来的数据转换为由若干个线性无关向量表示的新数据。这些新向量表示的数据不仅要求相互线性无关,而且需要所包含的信息量最大。

PCA使用方差来衡量新变量的信息量大小,按照方差大小排序依次为第一主成分、第二主成分等。

PCA的计算流程

numpy代码实现
import numpy as np
class PCA():
# 计算协方差矩阵
def calc_cov(self, X):
m = X.shape[0]
# 数据标准化
X = (X - np.mean(X, axis=0)) / np.var(X, axis=0)
return 1 / m * np.matmul(X.T, X)
def pca(self, X, n_components):
# 计算协方差矩阵
cov_matrix = self.calc_cov(X)
# 计算协方差矩阵的特征值和对应特征向量
eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)
# 对特征值排序
idx = eigenvalues.argsort()[::-1]
# 取最大的前n_component组
eigenvectors = eigenvectors[:, idx]
eigenvectors = eigenvectors[:, :n_components]
# Y=PX转换
return np.matmul(X, eigenvectors)
from sklearn import datasets
import matplotlib.pyplot as plt
# 导入sklearn数据集
iris = datasets.load_iris()
X = iris.data
y = iris.target
# 将数据降维到3个主成分
X_trans = PCA().pca(X, 3)
# 颜色列表
colors = ['navy', 'turquoise', 'darkorange']
# 绘制不同类别
for c, i, target_name in zip(colors, [0,1,2], iris.target_names):
plt.scatter(X_trans[y == i, 0], X_trans[y == i, 1],
color=c, lw=2, label=target_name)
# 添加图例
plt.legend()
plt.show() 
sklearn代码实现
from sklearn import datasets
import matplotlib.pyplot as plt
# 导入sklearn数据集
iris = datasets.load_iris()
X = iris.data
y = iris.target
# 导入sklearn降维模块
from sklearn import decomposition
# 创建pca模型实例,主成分个数为3个
pca = decomposition.PCA(n_components=3)
# 模型拟合
pca.fit(X)
# 拟合模型并将模型应用于数据X
X_trans = pca.transform(X)
# 颜色列表
colors = ['navy', 'turquoise', 'darkorange']
# 绘制不同类别
for c, i, target_name in zip(colors, [0,1,2], iris.target_names):
plt.scatter(X_trans[y == i, 0], X_trans[y == i, 1],
color=c, lw=2, label=target_name)
# 添加图例
plt.legend()
plt.show()
奇异值分解
numpy代码实现
import numpy as np
A = np.array([[0,1],[1,1],[1,0]])
#奇异值分解
u, s, vt = np.linalg.svd(A, full_matrices=True)
print(u.shape, s.shape, vt.shape)
print('左奇异矩阵',u)
print('右奇异矩阵',vt)
print('奇异矩阵',s)
# svd逆运算
c=np.dot(u[:,:2]*s,vt)
print(np.allclose(A,c))sklearn代码实现
# 导入sklearn截断SVD算法模块
from sklearn.decomposition import TruncatedSVD
# 导入SciPy生成稀疏数据模块
from scipy.sparse import random as sparse_random
# 创建稀疏数据X
X = sparse_random(10, 10, density=0.01, format='csr', random_state=42)
# 基于截断SVD算法对X进行降维,降维的维度为5,即输出前5个奇异值
svd = TruncatedSVD(n_components=5, n_iter=7, random_state=42)
svd.fit(X)
# 输出奇异值
print(svd.singular_values_)svd实现图像去噪
# 导入相关模块
import numpy as np
import os
from PIL import Image
from tqdm import tqdm
### 定义图像恢复函数,由分解后的矩阵恢复到原矩阵
def restore(u, s, v, K):
'''
输入:
u:左奇异矩阵
v:右奇异矩阵
s:奇异值矩阵
K:奇异值个数
输出:
np.rint(a):恢复后的矩阵
'''
m, n = len(u), len(v[0])
a = np.zeros((m, n))
for k in range(K):
uk = u[:, k].reshape(m, 1)
vk = v[k].reshape(1, n)
# 前k个奇异值的加总
a += s[k] * np.dot(uk, vk)
a = a.clip(0, 255)
return np.rint(a).astype('uint8')
# 读入待压缩图像
img = np.array(Image.open("./1.jpg", 'r'))
# 对RGB图像进行奇异值分解
u_r, s_r, v_r = np.linalg.svd(img[:, :, 0])
u_g, s_g, v_g = np.linalg.svd(img[:, :, 1])
u_b, s_b, v_b = np.linalg.svd(img[:, :, 2])
# 使用前50个奇异值
K = 5
# 恢复图像
for k in tqdm(range(1, K+1)):
R = restore(u_r, s_r, v_r, k)
G = restore(u_g, s_g, v_g, k)
B = restore(u_b, s_b, v_b, k)
I = np.stack((R, G, B), axis=2)
Image.fromarray(I).save('./hh.jpg')






















 342
342











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










