高等数学关于切线,法线,切平面,法平面的详细解释
简介
本文章主要对高数下几个切线和切平面的总结
文章内容
- 平面曲线的切线和法线
- 空间曲线的切线和法平面
- 曲面的切平面和法线
平面曲线的切线和法线
我们知道平面的切线的斜率也就是f(x) 的在该点的导数,那法线也就是f(x)导数的负分之一。也就是切线的斜率x法线的斜率等于-1;
图解

空间曲线的切线和法平面
- 参数方程情况
空间曲线我们知道,x,y,z 都极限接近某一点的斜率,所以参数方程表示的空间曲线所求的切线斜率比较好求。

然后切线和法平面就可以表示为,如下:

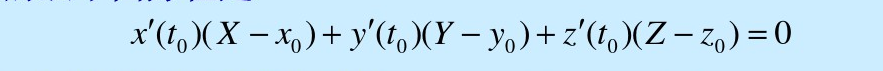
- 如果是空间曲线方程
例如 x = x ,y = y(x) , z = z(x); 那求切线和法平面比较简单

- 空间曲面的交线类型的空间曲线
这种情况还是对某一点偏导,举个下面的例子,下面例子怎么解,大家可以去看一下线性代数的克莱姆法则怎么解,挺简单,其实利用线性代数还可以解其他的,我还没复习到那里。


总结,我自己遇到的疑问
引用百度问答大佬的话:
因为空间曲面的切平面上,过切点的直线即切线有无数条,方向矢量各不相同,所以求之无意义。
反过来,一条曲线对应的切平面也有无数个,它们法矢量也不相同,所以求之也无意义
曲面的切平面和法线
其解释如下,主要用到法线和切线垂直,利用线性代数的正交。如下解释
总结
我也只是对这些常见的进行重新整理一下,还是要自己多做题才能够明白偷,希望自己2021考研上岸。

























 1232
1232

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








