曲线切线与曲面切面的求法

最新推荐文章于 2022-12-25 16:25:34 发布

格里芬阀门工

最新推荐文章于 2022-12-25 16:25:34 发布

阅读量7k

点赞数 4

分类专栏：高数空间解析几何多元函数微分学

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/qq_42578970/article/details/108123705

版权

高数同时被 3 个专栏收录

56 篇文章

订阅专栏

空间解析几何

9 篇文章

订阅专栏

多元函数微分学

8 篇文章

订阅专栏

曲线切线与法平面

显式形式：参数方程

$\left\{\begin{matrix} x=x(t)\\ y=y(t)\\ z=z(t) \end{matrix}\right. \right.$

则切线方向向量为(x'(t0),y'(t0),z'(t0))

隐式形式

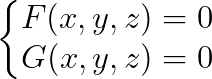
$\left\{\begin{matrix} F(x,y,z)=0\\ G(x,y,z)=0 \end{matrix}\right.$

则切线的方向向量为

法平面

已知曲线在(x0,y0,z0)的切线的方向向量为(xt,yt,zt)

则法平面方程为xt(x-x0)+yt(y-y0)+zt(z-z0)=0

曲面切面与法线

隐式形式

S:F(x,y,z)=0

则曲面在(x0,y0,z0)处的法向量为(Fx',Fy',Fz')

切平面方程为Fx'(x-x0)+Fy'(y-y0)+Fz'(z-z0)=0

显式形式

z=f(x,y)

将z=f(x,y)化为F(x,y,z)=f(x,y)-z

则法向量为(fx',fy',-1)

切平面方程为fx'(x-x0)+fy'(y-y0)-(z-z0)=0

法线

设曲面在(x0,y0,z0)处的法向量为(Fx,Fy,Fz)

则法线方程为

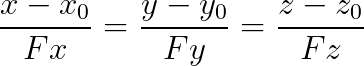
$\frac{x-x_{0}}{Fx}=\frac{y-y_{0}}{Fy}=\frac{z-z_{0}}{Fz}$

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。