考研数学 第9讲 一元积分的概念

最新推荐文章于 2024-12-11 06:13:26 发布
最新推荐文章于 2024-12-11 06:13:26 发布
阅读量2.4k 收藏 5
点赞数
分类专栏： 考研数学
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_40427276/article/details/106390287
版权

在这里插入图片描述

文章目录

一.概念

1.原函数与不定积分（加C常数）

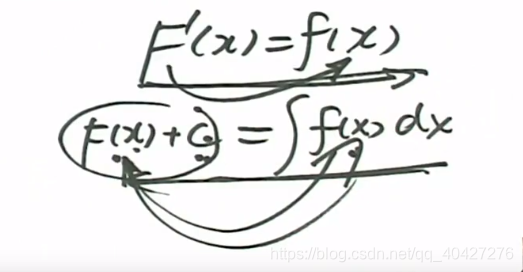
在这里插入图片描述
在这里插入图片描述

2.不定积分存在定理

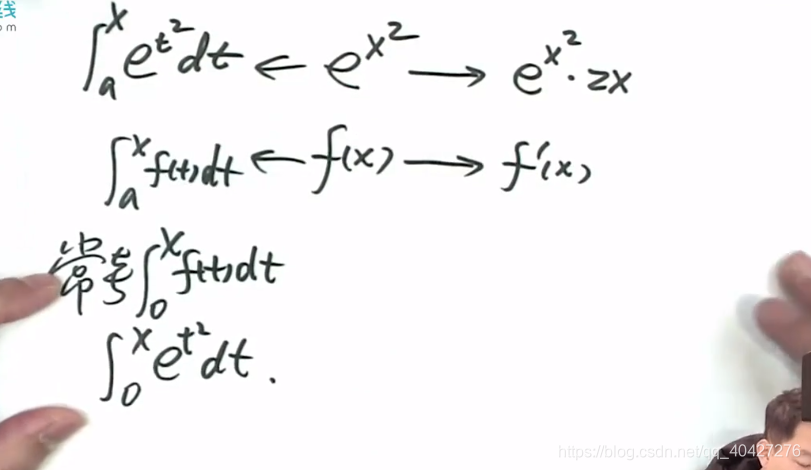
在这里插入图片描述

祖孙三代关系

在这里插入图片描述

例1.8.1 证明原函数（不定积分）存在定理

在这里插入图片描述

积分的拆分

积分上下限可以拆分，如a,b,c,在a~c上的函数积分可以拆分为a-b的积分加上b到c的积分

函数积分导函数直接奇偶传递

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

例1.8.6 证明

在这里插入图片描述

例1.8.7（积分函数的周期性）

一个周期的积分不变，与其起点无关，保证首尾不变，中间可随意拆分
在这里插入图片描述

例1.8.8

在这里插入图片描述

一个函数可导它的导函数（不可突变）

在这里插入图片描述

（二）定积分

1.定积分的概念

在这里插入图片描述

积分的精确定义（曲边梯形面积推导）

在这里插入图片描述
在这里插入图片描述

考试时准确定义的一般形式 a=0，b=1（0-1上定积分）

在这里插入图片描述

例 1.8.23 （提出1/n，凑i/n的形式）

在这里插入图片描述

例1.8.24（凑i/n）

在这里插入图片描述
在这里插入图片描述

2.定积分存在定理

在这里插入图片描述
主要是1，3

3.定积分的性质

在这里插入图片描述

4.保号性

在这里插入图片描述
注意下方的等号一般是取不到的，除非上方是恒等式
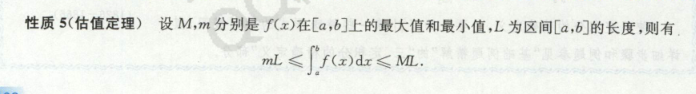
在这里插入图片描述

5.估值定理

在这里插入图片描述

6.中值定理

在这里插入图片描述
在这里插入图片描述

三.变限积分（重点在于其求导公式）

在这里插入图片描述

四.反常积分

在这里插入图片描述
在这里插入图片描述

2.无穷区间上的反常积分

在这里插入图片描述
在这里插入图片描述

3.无界函数的反常积分

在这里插入图片描述
在这里插入图片描述

二.基本积分公式

在这里插入图片描述
在这里插入图片描述

四大积分法

在这里插入图片描述

1.凑微分法（第一类换元法）

在这里插入图片描述

2.换元法

在这里插入图片描述

三角函数代换

在这里插入图片描述

例1.8.12

在这里插入图片描述

其他代换方法

在这里插入图片描述

3.分部积分法

在这里插入图片描述

推导过程

在这里插入图片描述

在这里插入图片描述

口诀：反对幂指三（三指）

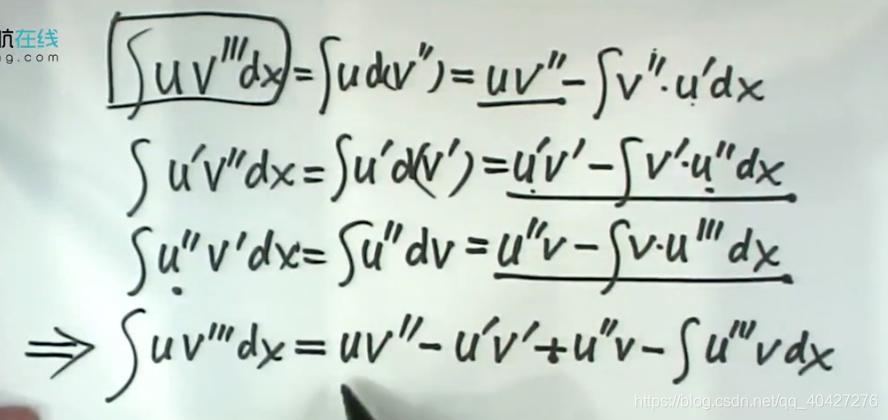
在这里插入图片描述
在这里插入图片描述

分部积分的推广

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

表格法
循环积分法

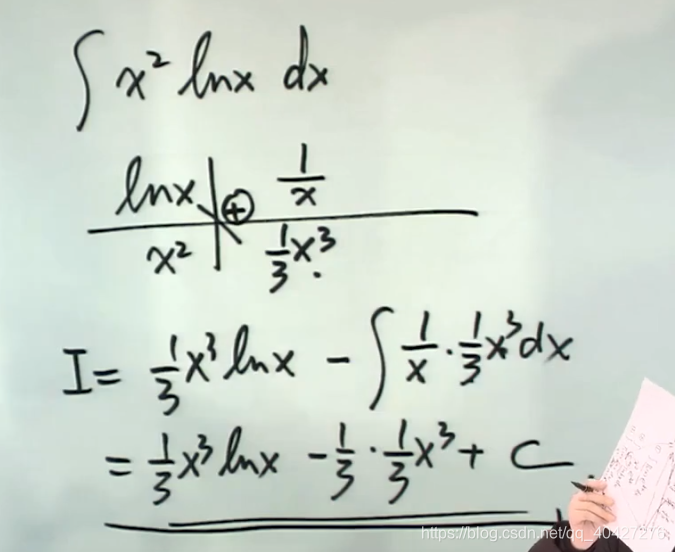
在这里插入图片描述
在这里插入图片描述

例1.8.17（换元+分部积分）

在这里插入图片描述

4.有理函数的积分（分解因式）

先对分母因式分解
根据因式阶数拆分（注意分解原则）
通分求A1-An（待定系数法）
在这里插入图片描述

例1.8.21

在这里插入图片描述

定积分的计算

在这里插入图片描述

1.定积分的换元法

在这里插入图片描述

2.定积分的分部积分法

在这里插入图片描述
在这里插入图片描述
注意有用的结论可直接简化

例 1.8.29 区间再现法（可独立于基本积分法使用适用于含三角函数的积分）

在这里插入图片描述

例1.8.32

在这里插入图片描述
在这里插入图片描述

例1.10.5（区间再现 令x=a+b-t)

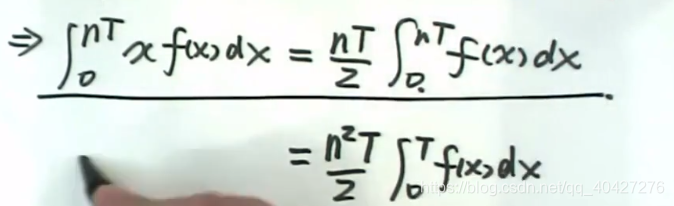
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

例1.8.33 华里士公式（计算高阶三角函数积分十分方便）–点火公式

在这里插入图片描述

例1.8.30

在这里插入图片描述

例1.8.33，1.8.34 点火公式推广

在这里插入图片描述

【微服务】springboot 适配多数据源设计与实现
congge
07-04 6999
springboot多数据源配置详解
Spring Cloud Alibaba系列之分布式事务Seata
Nicky's blog
01-07 2454
Spring Cloud Alibaba系列之分布式事务Seata。Seata是Alibaba开源的一款分布式事务解决方案框架，致力于提供简单易用，高性能的服务。Seata支持多种分布式事务解决方法，比如常见的TCC、XA、SAGA，同时还有独创的AT模式
Seata 2.x 系列【11】多数据源分布式事务
记录知识、锤炼自我
03-15 1903
在之前的案例中，我们在Spring Cloud微服务场景下使用Seata解决了分布式事务问题，在单体架构中，单个服务也可能存在跨库导致的分布式事务问题，例如下图中，因为分库导致下单请求需要连接多个数据库进行操作：
动态多数据源使用seata实现分布式事务
IT巅峰技术专栏
12-03 4516
一、背景 目前公司很多应用因为历史原因，一个应用访问多个数据库进行插入和更新操作，这就可能产生数据一致性问题，同时应用如果跨服务的调用也可能会产生事务问题。 目前应用是采用dynamic-datasource-spring-boot-starter做多数据源控制的。而seata是一款开源的分布式事务框架。我们了解到dynamic-datasource-spring-boot-starter的新版本已经支持基于seata的分布式事务了，而官网的例子基本都是标准的单数据源的整合，下面我们分别对dynam..
分布式事务 Seata(四) 多数据源事务
x37558670的博客
03-31 1811
项目搭建 我搭建的是一个最基础的用户下单，减库存，减用户金额，创建订单的一个微服务框架。因为后面需要测试微服务下的分布式事务，这里测试的是 多数据源 下的分布式事务。 项目结构如下: |-- demo |-- entity 实体对象(为了让其他服务拥有所有服务对象) |-- order 订单 (pom导入了 entity ) |-- stock 库存 (pom导入了 entity ) |-- user 用户 (pom导入了 entity ) 这里使用了mybatis-plus的相关技术，不
springcloud alibaba mybatis-plus多数据源集成seata分布式事务
hlvy
03-22 1895
注意以上mybatis集成seata主要是把数据源给了seata的代理类DataSourceProxy。最后在2边的方法上面加上@GlobalTransactional注解就行了。nacos对应的seata-server.properties 配置。在所需要分布式事务的库创建undo_log表 每个数据源库都需要。B项目:同A项目mybatis+seata配置。A项目mybatis+seata配置。注意:这里不讲解seata的搭建。........此处同A项目配置。这里使用的是默认的AT模式。
【微服务】第17节：分布式事务、集成Seata
m0_46013789的博客
06-15 1118
解决分布式事务的方案有很多，但实现起来都比较复杂，因此我们一般会使用开源的框架来解决分布式事务问题。在众多的开源分布式事务框架中，功能最完善、使用最多的就是阿里巴巴在2019年开源的Seata了。
【SpringCloud】使用Seata实现分布式事务
Transient_的博客
03-17 1534
介绍了Seata框架的基本架构，Seata各组件的各自功能。以及如何在项目中使用Seata框架实现分布式事务。
SpringCloud Alibaba之Seata分布式事务
m0_55849656的博客
07-08 783
事务事务指的就是一个操作单元，在这个操作单元中的所有操作最终要保持一致的行为，要么所有操作都成功，要么所有的操作都被撤销。
【SpringCloud】微服务4—分布式事务
m0_73509988的博客
07-22 2752
XA 规范 是 X/Open 组织定义的分布式事务处理（DTP，Distributed Transaction Processing）标准，XA 规范 描述了全局的TM与局部的RM之间的接口，几乎所有主流的数据库都对 XA 规范 提供了支持。的原则，归其原因就是参与事务的多个子业务在不同的微服务，跨越了不同的数据库。虽然每个单独的业务都能在本地遵循ACID，但是它们互相之间没有感知，不知道有人失败了，无法保证最终结果的统一，也就无法遵循ACID的事务特性了。OK，至此为止，微服务整合的工作就完成了。
springboot mybatis 集成多数据源 两种实现方式
09-12
springboot mybatis 集成多数据源 两种实现方式，一种静态添加，一种动态添加，后者能够支持很好的拓展。使用注解的方式实现，项目打包了一个module
微服务 高并发 多数据源 读写分离 分库分表
zhaoyang10的专栏
03-11 1681
数据库分库分表策略的具体实现方案 https://mp.weixin.qq.com/s?__biz=MzUxOTAxODc2Mg==&mid=2247483791&idx=4&sn=d96a8696003bf193f2250d9fe266106a&chksm=f98141eacef6c8fccb3b01c9b7b787b96ed25f8fa51974c5a2e375...
分布式事务解决方案Seata实战（SpringBoot多数据源）及其原理剖析
沮丧的南瓜
12-22 5109
文章目录一、分布式解决方案Seata介绍1.1 什么是Seata1.2 Seata的三大角色1.3 AT模式设计思路第一阶段第二阶段整体执行流程1.4 设计亮点1.5 存在的问题性能损耗性价比全局锁二、Seata实战 - 快速开始2.1 Seata Server（TC）环境搭建2.2 db存储模式+Nacos(注册&配置中心)部署步骤一：下载安装包步骤二：建表(仅db模式)步骤三：修改store.mode步骤四：修改数据库连接步骤五：配置Nacos注册中心步骤六：配置Nacos配置中心步骤七：启动S
【分享】微服务合并之多数据源整合（Dynamic Datasource）和Flyway对多数据源进行数据库脚本管理
码农阿福的博客
05-09 1788
在工作中，我们使用**Flyway**对数据库进行版本管理，每个微服务都有各自的数据库。最近我们需要对三个微服务合并成一个服务，且保留数据库不合并，有以下改动要求： 1. 在不影响功能正常使用的情况下对代码结构尽量改动小 2. 尽可能短的开发周期 3. “分久必合，合久必分”，方便后面对服务的拆分 - 三个工程包合并成一个大包，可以通过具体的子包名区分以前的三个服务 - Flyway脚本分开管理，单独作用在三个文件夹对应以前三个工程 - 引入多数据源（Dynami
SpringBoot+Seata在多数据源和feign中的简单使用
qq_45367825的博客
03-03 1420
SpringBoot+Seata在多数据源和feign中的简单使用
Seata入门系列(25)-Seata集成Mybatis-Plus多数据源
记录知识、锤炼自我
03-03 2349
文章目录前言问题场景使用Seata 解决多数据源事务问题1. 集成Nacos Seata2. 多数据源集成Seata3. 测试 前言 在使用单个服务，多数据源时，也存在分布式事务问题。 当单体系统需要访问多个数据库（实例）时就会产生分布式事务。 比如：用户信 息和订单信息分别在两个MySQL实例存储，用户管理系统删除用户信息，需要分别删除用户信息及用户的订单信 息，由于数据分布在不同的数据实例，需要通过不同的数据库链接去操作数据，此时产生分布式事务。 简言之：跨 数据库实例产生分布式事务。 问题场景 参考
springboot实现多数据源
weixin_45934981的博客
01-02 3039
在当今复杂多变的应用场景下，对多数据源的需求日益增长。特别是在微服务架构和分布式系统中，同时连接多个数据库成为一种常见的业务需求。为了应对这一挑战，本文将探讨如何在Spring Boot应用中利用MyBatis框架实现多数据源的灵活配置。通过逐步引导读者完成关键步骤，我们将深入了解如何配置不同的数据源、管理事务，以及在MyBatis的Mapper接口和XML文件中定义清晰而模块化的SQL操作。这不仅提高了系统的可维护性，还为开发者们提供了更为灵活和高效的数据访问解决方案。
若依框架二次开发——若依微服务中配置 MySQL + DM 多数据源
最新发布
bjzhang75的博客
12-11 1902
若依微服务中配置 MySQL + DM 多数据源
SpringCloud Alibaba Seata处理分布式事务的需求分析
06-09
SpringCloud Alibaba Seata是一个开源的分布式事务解决方案，它能够帮助开发者轻松地解决分布式事务的问题。在分布式微服务架构中，由于服务之间的调用涉及到多个数据库的操作，因此需要使用分布式事务来保证数据的一致性。SpringCloud Alibaba Seata能够解决以下几个方面的需求： 1. 分布式事务的一致性问题。Seata通过对多个数据源的操作进行统一的事务管理，保证各个数据源之间的操作是原子性的，即要么全部成功，要么全部失败。 2. 跨服务的事务管理。由于微服务架构中服务之间的调用是通过网络实现的，因此需要使用分布式事务来解决服务之间的事务问题。Seata能够通过全局事务管理器来实现不同服务之间的事务协调。 3. 高可用性和可靠性。Seata具有高可用性和可靠性，并且支持多种分布式事务模型，包括TCC、SAGA和XA等，能够满足不同场景下的需求。 4. 与SpringCloud集成。Seata与SpringCloud框架集成紧密，能够方便地与SpringCloud项目进行集成，提供了完整的SpringCloud生态支持。 综上所述，SpringCloud Alibaba Seata是一个功能强大的分布式事务解决方案，能够帮助开发者轻松地解决分布式事务的问题。
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值