MATLAB中的rand()和randn()函数

在Matlab中，rand是0-1的均匀随机分布，而randn是均值为0方差为1的正态分布。

1.rand()是0-1的均匀随机分布

介绍

例子

举个例子：X = rand 产生一个在（0，1）区间内的随机数。

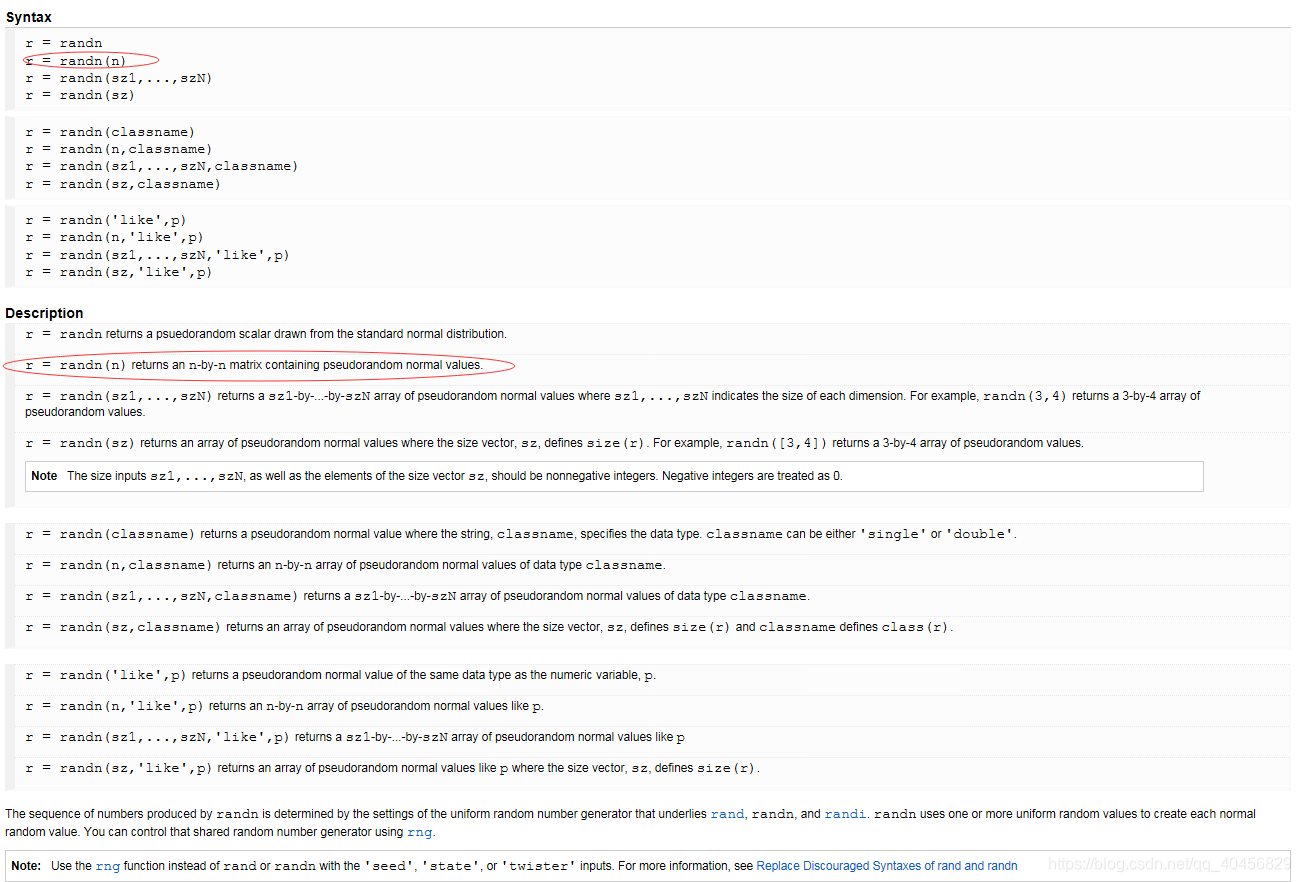
X = rand(n)或X = randn(n)产生一个n*n的随机变量矩阵。

X = rand(m,n)或X = randn(m,n)产生一个m*n的随机变量矩阵。

2.randn()是均值为0方差为1的标准正态分布

介绍

例子

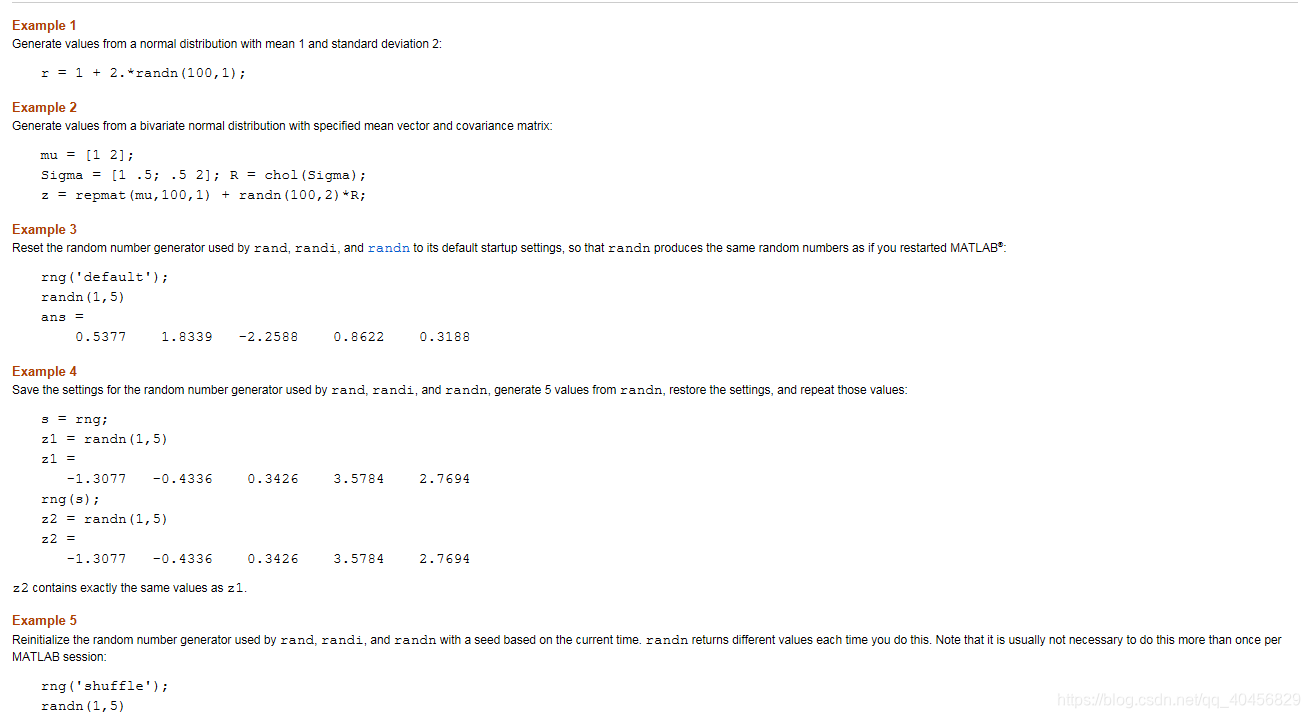
3.正态分布（Normal Distribution）

  正态分布（Normal distribution），也称“常态分布”，又名高斯分布（Gaussian distribution），最早由A.棣莫弗在求二项分布的渐近公式中得到。C.F.高斯在研究测量误差时从另一个角度导出了它。P.S.拉普拉斯和高斯研究了它的性质。是一个在数学、物理及工程等领域都非常重要的概率分布，在统计学的许多方面有着重大的影响力。

正态曲线呈钟型，两头低，中间高，左右对称因其曲线呈钟形，因此人们又经常称之为钟形曲线。

若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布，记为N(μ，σ^2)。其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。

 

3.1 正态分布标准化变换

3.2 正态分布公式

3.3 正态分布性质

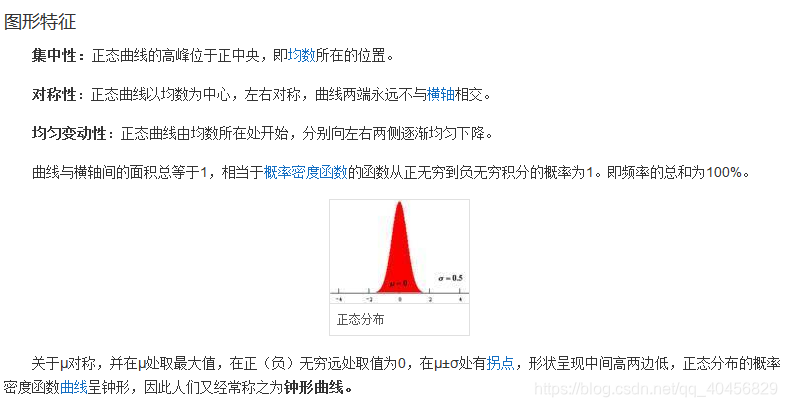
3.4 正态分布的应用

1. 1.频数分布以及概率估计。
2. 2.制定参考值范围，包括正态分布法和百分位数法。
3. 3.质量控制，SPC技术应用的核心。
4. 4.正态分布是检验、方差分析、相关和回归分析等多种统计方法的理论基础。

3.5 中心极限定理（Central Limit Theorem）

中心极限定理指的是给定一个任意分布的总体。我每次从这些总体中随机抽取 n 个抽样，对这n个抽样取平均值，总共抽取关计算 m 次。 则这m个平均值数据分布接近正态分布。正态分布的直观理解请参考正态分布初步理解。

4.正态分布MATLAB画法

首先给出正态分布概率密度函数（The normal distribution probability density function）的公式和标准正态分布概率密度函数的公式，然后通过normpdf( )生成标准正态分布概率密度函数的数据，然后通过plot( )绘制标准正态分布概率密度函数的图形。

4.1 正态分布概率密度函数的公式如下图。其中，μ为平均值（mean），σ为标准差（standard deviation）。

4.2 当μ=0，σ=1时，第一步中的正态分布为标准正态概率密度函数，如下图。

4.3 启动MATLAB，新建脚本（Ctrl+N），输入如下代码：

其中normpdf(x,0,1)是用来产生μ=0，σ=1的标准正态分布概率密度函数的数据。

close all; clear all; clc

x=-1:.1:1;

norm=normpdf(x,0,1);

figure('Position',[50,50,600,500],'Name','Normal PDF',...

    'Color',[1,1,1]);

plot(x,norm,'r-','LineWidth',3)

set(gca,'FontSize',10,'TickDir','out','TickLength',[0.02,0.02])

xlabel('X','FontSize',15);ylabel('PDF','FontSize',15)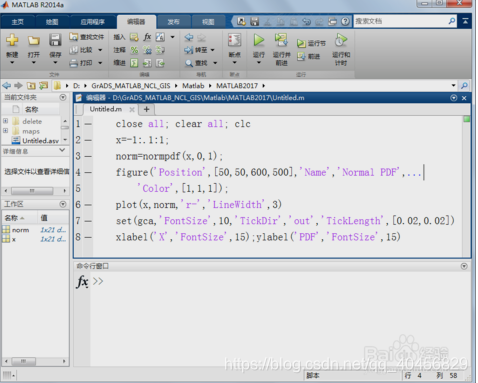

4.4 保存和运行上述脚本，在工作区（Workspace）得到标准正态分布概率密度函数的数据norm，双击norm可以查看数据具体内容。

4.5  同时得到如下μ=0，σ=1的标准正态分布概率密度函数图形。

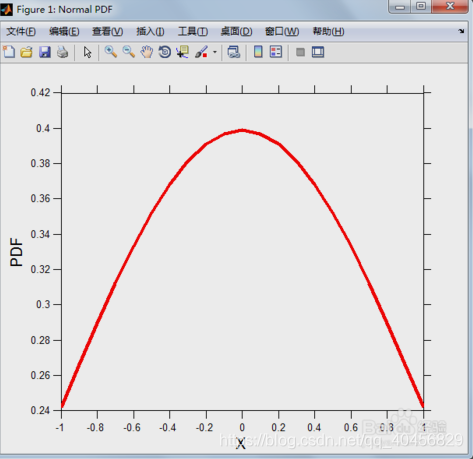
具体请参考MATLAB绘制正态分布。