算法的时间复杂度定义为:
时间复杂度或称时间复杂性,又称计算复杂度,她说是算法有效的度量之一,时间复杂度是一个算法运行时间的相对度量,一个算法的运行时间长短,它大致等于执行一种简单操作所(赋值、比较、计算、转向、返回、输入和输出)需要的时间与算法中进行简单操作次数的乘积。
根据定义,求解算法的时间复杂度的具体步骤是:
⑴ 找出算法中的基本语句;
一般算法中执行次数最多的那条语句就是基本语句,通常是最内层循环的循环体。
⑵ 计算基本语句的执行次数的数量级;
只需计算基本语句执行次数的数量级,这就意味着只要保证基本语句执行次数的函数中的最高次幂正确即可,可以忽略所有低次幂和最高次幂的系数。这样能够简化算法分析,并且使注意力集中在最重要的一点上:增长率。
⑶ 用大Ο记号表示算法的时间性能。
当n趋近于无穷大时,如果lim(T(n)/f(n))的值为不等于0的常数,则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n))。
简单的说,就是保留求出次数的最高次幂,并且把系数去掉。 如T(n)=2n^2+n+1=O(n^2)
需要注意的是:for语句由于会加到n+1会执行n+1次,而它的函数体由于i==n+1时2不满足判断条件只执行n次
要看清楚题目中问的是for语句的执行次数,还是它的循环体执行的次数
#include "stdio.h"
int main()
{
int i, j, x = 0, sum = 0, n = 100; /* 执行1次 */
for( i = 1; i <= n; i++) /* 执行n+1次 */
{
sum = sum + i; /* 执行n次 */
for( j = 1; j <= n; j++) /* 执行n*(n+1)次 */
{
x++; /* 执行n*n次 */
sum = sum + x; /* 执行n*n次 */
}
}
printf("%d", sum); /* 执行1次 */
} 照上面推导“大O阶”的步骤,我们来看
第一步:“用常数 1 取代运行时间中的所有加法常数”,
则上面的算式变为:执行总次数 =3n^2 + 3n + 1
(直接相加的话,应该是T(n) = 1 + n+1 + n +n*(n+1) + n*n + n*n + 1 = 3n^2 + 3n + 3。现在用常数 1 取代运行时间中的所有加法常数,就是把T(n) =3n^2 + 3n + 3中的最后一个3改为1. 就得到了 T(n) = 3n^2 + 3n + 1)
第二步:“在修改后的运行次数函数中,只保留最高阶项”。
这里的最高阶是 n 的二次方,所以算式变为:执行总次数 = 3n^2
第三步:“如果最高阶项存在且不是 1 ,则去除与这个项相乘的常数”。
这里 n 的二次方不是 1 所以要去除这个项的相乘常数,算式变为:执行总次数 = n^2
因此最后我们得到上面那段代码的算法时间复杂度表示为: O( n^2 )
下面我把常见的算法时间复杂度以及他们在效率上的高低顺序记录在这里,使大家对算法的效率有个直观的认识。
O(1) 常数阶 < O(logn) 对数阶 < O(n) 线性阶 < O(nlogn) < O(n^2) 平方阶 < O(n^3) < { O(2^n) < O(n!) <O(n^n) }
最后三项用大括号把他们括起来是想要告诉大家,如果日后大家设计的算法推导出的“大O阶”是大括号中的这几位,那么趁早放弃这个算法,在去研究新的算法出来吧。因为大括号中的这几位即便是在 n 的规模比较小的情况下仍然要耗费大量的时间,算法的时间复杂度大的离谱,基本上就是“不可用状态。
好了,原理就介绍到这里了。下面通过几个例子具体分析下时间复杂度计算过程。
一、计算 1 + 2 + 3 + 4 + ...... + 100。
常规代码:
#include "stdio.h"
int main()
{
int i, sum = 0, n = 100; /* 执行1次 */
for( i = 1; i <= n; i++) /* 执行 n+1 次 */
{
sum = sum + i; /* 执行n次 */
//printf("%d \n", sum);
}
printf("%d", sum); /* 执行1次 */
}
从代码附加的注释可以看到所有代码都执行了多少次。那么这写代码语句执行次数的总和就可以理解为是该算法计算出结果所需要的时间。该算法所用的时间(算法语句执行的总次数)为: 1 + ( n + 1 ) + n + 1 = 2n + 3
而当 n 不断增大,比如我们这次所要计算的不是 1 + 2 + 3 + 4 +...... + 100 = ? 而是 1 + 2 + 3 + 4 + ...... + n = ?其中 n 是一个十分大的数字,那么由此可见,上述算法的执行总次数(所需时间)会随着 n 的增大而增加,但是在 for 循环以外的语句并不受n 的规模影响(永远都只执行一次)。所以我们可以将上述算法的执行总次数简单的记做: 2n 或者简记 n
这样我们就得到了我们设计的算法的时间复杂度,我们把它记作: O(n)。
高斯算法:
#include "stdio.h"
int main()
{
int sum = 0, n = 100; /* 执行1次 */
sum = (1 + n) * n/2; /* 执行1次 */
printf("%d", sum); /* 执行1次 */
}
这个算法的时间复杂度: O(3),但一般记作 O(1)。
从感官上我们就不难看出,从算法的效率上看,O(1) < O(n) 的,所以高斯的算法更快,更优秀。
二、求两个n阶方阵C=A*B的乘积其算法如下:
//右边列为语句执行的频度
void MatrixMultiply(int A[n][n],int B [n][n],int C[n][n])
{
for(int i=0; i <n; i++) //n+1
{
for (j=0;j < n; j++) //n*(n+1)
{
C[i][j]=0; //n^2
for (k=0; k<n; k++) //n^2*(n+1)
{
C[i][j]=C[i][j]+A[i][k]*B[k][j]; //n^3
}
}
}
}
则该算法所有语句的频度之和为:
T(n) = 2n^3+3n^2+2n+1; 利用大O表示法,该算法的时间复杂度为O(n^3)。
三、分析下列时间复杂度
void test_(int n)
{
i = 1, k = 100;
while (i<n)
{
k = k + 1;
i += 2;
}
}
设for循环语句执行次数为T(n),则 i = 2T(n) + 1 <= n - 1, 即T(n) <= n/2 - 1 = O(n)
四、分析下列时间复杂度
《1》
int i,j, n = 100;
for(i = 0; i < n; i++){
for(j = i; j < n; j++){/*注意 j = i 而不是0*/
/*时间复杂度为 O(1)的程序步骤序列*/
}
}
由于当 i= 0时,内循环执行了n次,当 i =1时,执行了n-1次,……当i=n一1时,执行了1次。所以总的执行次数为:
n+(n-1)+(n-2)+…+ 1= = O(n^2)
《2》
void test_2(int b[], int n)
{
int i, j, k;
for (i=0; i<n-1; i++)
{
k = i;
for (j=i+1; j<n; j++)
{
if (b[k] > b[j])
{
k = j;
}
}
x = b[i];
b[i] = b[k];
b[k] = x;
}
}
其中,算法的基本运算语句是:
if (b[k] > b[j])
{
k = j;
}时间复杂度为O(1)
执行次数为:n-1 + n-2 + ... + 1 = = O(n^2)
《3》三次循环
for(int i=0;i<N;i++)
{
for(int j=i;j<N;j++)
{
//此处运行次数N+N-1+N-2+...+1=1+2+3+...+N=N(N+1)/2
for(int k=j;k<N;k++)
{
//此处运行次数:N(N+1)/2+(N-1)*N/2+...+2*3/2+1*2/2=N(N+1)(N+2)/6
}
}
}参考:for循环三层嵌套 时间复杂度计算_三层for循环的时间复杂度_liulangcheshou的博客-CSDN博客
for循环时间复杂度算法理解_for循环的时间复杂度_冰冰心的博客-CSDN博客
补充数学公式
《4》
for(i = 2;i <= n;++i) //执行n次
for(j = 2;j <= i-1;++j) //执行(n-1)n次
{
++x; //执行(n-2)(1 + n-2)/2次
a[i][j] = x;
}
分析 ++x 的执行次数:当 i = 3 时,才会执行内层循环体;所以j相当于从 0——n-1 ;外层循环体执行 n-1 次
五、分析下列时间复杂度
void test_3(int n)
{
int i = 0, s = 0;
while (s<n)
{
i++;
s = s + i;
}
}
其中,算法的基本运算语句即while循环内部分,
设while循环语句执行次数为T(n),则
六、Hanoi(递归算法)时间复杂度分析
void hanoi(int n, char a, char b, char c)
{
if (n==1)
{
printf("move %d disk from %c to %c \n", n, a, c); //执行一次
}
else
{
hanoi(n-1, a, c, b); //递归n-1次
printf("move %d disk from %c to %c \n", n, a, c); //执行一次
hanoi(n-1, b, a, c); //递归n-1次
}
}
对于递归函数的分析,跟设计递归函数一样,要先考虑基情况(比如hanoi中n==1时候),这样把一个大问题划分为多个子问题的求解。
故此上述算法的时间复杂度的递归关系如下:










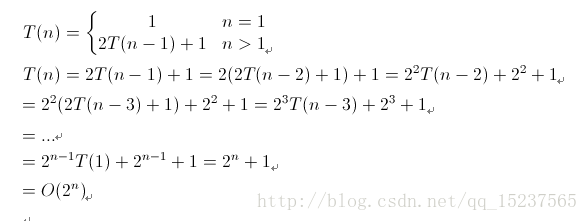














 235
235











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










