启发式搜索求解八数码问题（Java实现，八数码小项目已开源）

问题的定义

又称九宫问题。在3×3的棋盘上，摆有八个棋子，每个棋子上标有1至8的某一数字，不同棋子上标的数字不相同。棋盘上还有一个空格，空格可以不超过边界地上下左右移动。

要求解决的问题是：以启发式搜索方法求解给定初始状态和目标状态的最优搜索路径。
例如，那么空格应该向上走一步：

问题的解决

解的表示

将九宫格中数字从上到下、从左到右顺序排列后形成一个9个数字的序列（空格用0表示）来标识九宫格的一种状态。那么初始状态为：

1	2	3	4	0	5	6	7	8

目标状态为：

1	0	3	4	2	5	6	7	8

那么如何唯一的确定一个状态？这里用到了康托展开。

康托展开

cantor展开的公式：
$$X=a_n\ast (n-1)!+a_{n-1}\ast (n-2)!+a_{n-1}\ast (n-3)!+...+a_1\ast 0!$$
其中，$a_i$为整数，且$0<=a_i<i,1<=i<=n$。

$a_i$表示原数的第i位在当前未出现的元素中是排在第几个。

康拓展开可以求一个排列是所有排列中的第几大，给排列分配了一个唯一的id。

---

例如：$（1,2,3）$组成的排列，怎样知道$x=213$是所有排列中的第几大的数？

• $a_1=2$，比2小的只有1，那么小于2开头的数有$1\ast 2!$个。第一个数固定是1，第二个数有两种可能的情况，第三个数只有一种情况。
  
• $a_2=1$，比1小的数没有（1~n的排列），那么小于第二位为1的数有$0\ast 1！$
• 因此小于213的$(1,2,3)$排列数有$1\ast 2!+0\ast 1!=2$个，可知213是第3大的数，可以认为数213的id为2。
• $1\ast 2!+0\ast 1!=2$就是一个康托展开式，实现了全排列到自然数的双向映射。

---

const int factorial[]={1,1,2,6,24,120,720,5040,40320,362880,3628800};//阶乘0-10
//cantor展开,n表示是n位的全排列，num[]表示全排列的数（用数组表示）
int cantor(int num[],int n){
    int ans=0,sum=0; //sum中存放a[i]的值
    for(int i=1;i<n;i++){
        for(int j=i+1;j<=n;j++)
            if(num[j]<num[i])
                sum++;
        ans+=sum*factorial[n-i];//累积
        sum=0;//计数器归零
    }
    return ans+1;
}

逆康托展开

知道一个排列是第几大的数，同样可以反过来求出这个排列是什么。
但是注意反向求时用的是id，而不是第几大。比如刚刚的213是第3大的数，id是2。
那么对排列(1, 2, 3)，$n=3$ 和$id=2$做逆康托展开：

• $2/2!=1$余0，则$a_3=1$，可知比第一位小的数有1个，所以首位为2
• $0/1!=0$余1，则$a_2=1$，比第二位小的数有0个，所以第二位为1
• 自然最后一个数就是3了
• 得到了213，实现了十进制数到全排列的双射

//康托展开逆运算
void decantor(int x, int n)
{
    vector<int> v;  // 存放当前可选数
    vector<int> a;  // 所求排列组合
    for(int i=1;i<=n;i++)
        v.push_back(i);
    for(int i=n;i>=1;i--)
    {
        int r = x % factorial[i-1];
        int t = x / factorial[i-1];
        x = r;
        sort(v.begin(),v.end());// 从小到大排序
        a.push_back(v[t]);      // 剩余数里第t+1个数为当前位
        v.erase(v.begin()+t);   // 移除选做当前位的数
    }
    for(int i=0; i<a.size(); i++){
    	cout<<a[i]<<" "; 
	}
}

---

那么就可以把每个状态用一个十进制数id来表示了，并能够方便的判断两个状态是否相同，搜索过程中经常要判断是否搜索到了目标状态。

需要注意的是，因为空格我是用0表示，所以康托展开和逆康托展开是对于0到n-1的排列做，和1到n的计算过程有一点点区别，当然也可以直接用9表示空格。

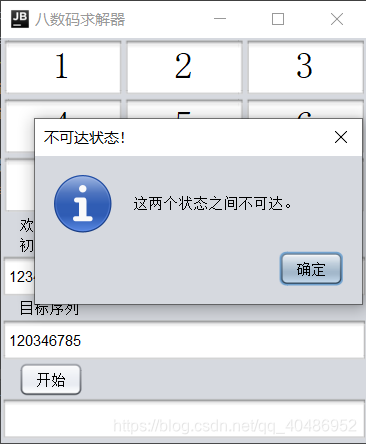
不可达状态的识别

如果用户输入的初始状态和目标状态本身不可达，而我们又能提前识别出这种不可达情况，就可以避免很多无谓的尝试和计算。

可以用两个状态的序列逆序值的奇偶性来判断是否可达。注意判断逆序性时不考虑0。

• 数的逆序值：位于这个数前面的比这个数大的数的个数。
• 序列的逆序值：数列中每个数的逆序值之和

比如：

序列值	2	3	1	5	8	4	6	7
逆序值	0	0	2	0	0	2	1	1

那么这个序列的逆序值就是$0+0+2+0+0+2+1+1=6$

结论：
如果两个状态的数字序列的逆序值奇偶性一致，则两状态互相可达。

证明肯定是不会证明的…

启发函数

启发式搜索就是利用知识来引导搜索，尽量避免搜索无效的搜索、减少搜索范围，降低时间复杂度。启发信息的强弱对搜索的过程有重大影响。

对于九宫格问题启发信息一般有两种，分别是：

• 取目标状态与当前状态相同的节点个数
• 当前状态每个结点到目标状态相应结点所需步数的总和（曼哈顿距离）

感觉两个都比较合理，但是第二个更加合适。

因为在第一种算出来相同的情况下，往往需要再看第二种谁的步数总和小说明哪个解更优秀。

open表和close表

• open表中用来记录考察过的点
• close表中用来记录当前待考察的点

因为已经实现了每个状态都用一个十进制数id标识，那么open表用一个int型的数组就可以了。

而close表需要时刻按照待考察的解的启发信息高低来排序，比较适合存在一个堆里。

其他

为了最后输出步骤，需要一个int型数组parent来指示这个状态是怎样从前一个状态到达的，也就是走的方向，故需要记录前驱结点信息（包括id和方向；

为了中间的搜索过程能够动态展示出来，开启了新线程控制组件更新。
Java Swing开启多线程实现实时内容更新

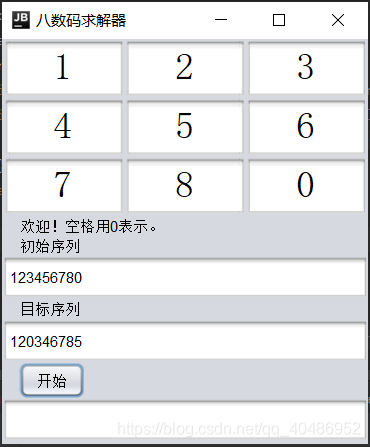
搜索过程

参考文档

结果演示

数字会随着指令移动。

源代码

Java实现（IDE为IDEA），已上传至github