MOEA/D 算法详解

---

1 聚合方法

1.1 权重求和法 (Weighted Sum Approach)

$$\begin{gathered} maximize{g}^{ws}(x/\lambda )=\sum _{i=1}^m{\lambda }_i{f}_i(x) \\ subjecttox\in \Omega \end{gathered}$$

权重求和法的意义在于, 我们不需要去考虑多个目标函数值的优化, 而是为每个目标函数根据重要程度分配一个恰当的权重, 也即 ${\sum }_{i=0}^m{\lambda }^i=1$ 。 然后根据目标函数 $f_i$ 的重要程度进行不同程度的优化来获取 max/min 的函数值。

---

1.2 切比雪夫聚合法 (Tchebycheff Approach）

公式
m i n i m i z e    g t e ( x ∣ λ , z ∗ ) = m a x 1 ≤ i ≤ m { λ ∣ f i ( x ) − z i ∗ ∣ } s . t . x ∈ Ω minimize \ \ g^{te}(x|\lambda,z^*) = \mathop{max}\limits_{1\le i \le m} \{\lambda |f_i(x)-z^*_i|\} \\ s.t. x\in \Omega minimize  gte(x∣λ,z∗)=1≤i≤mmax​{λ∣fi​(x)−zi∗​∣}s.t.x∈Ω

切比雪夫方法思路在于不断迫使个体接近预定的理想点, 最终到达约束条件 $\Omega$ 下的 Pareto 最优解。算法的精髓在于通过聚合函数把多目标优化问题转化为单目标优化。

对于上述公式提出的多目标优化问题, 求最小值, 种群规模为m, 解析如下:

$z^{\ast }=(z_1^{\ast },z_2^{\ast },...,z_m^{\ast })$ 为一系列参考点( 理想点 ) , 该点不一定实际存在, 如上图所示, 该点仅仅为了指出函数优化的方向, 也即理想状态, 用数学语言描述即对任意 i = 1 , 2 , . . . , m   均 有 z i ∗ ≤ m i n { f i ( x ) ∣ x ∈ Ω } i=1,2,...,m \ 均有 z_i^* \le min\{f_i(x)|x\in\Omega\} i=1,2,...,m 均有zi∗​≤min{fi​(x)∣x∈Ω} 。

${\lambda }^{\ast }=({\lambda }^1,{\lambda }^2,...,{\lambda }^m)$ 为一系列权重指标, 其中 ${\sum }_{i=0}^m{\lambda }^i=1$ 。 以下面图为例 $w_i等价{\lambda }_i$ ，权重的数量与种群规模相同，种群规模是m，那么权重的数量就是m。每组权重向量将多目标优化问题转化为一个单目标优化问题。m组权重向量就是m个单目标优化问题。

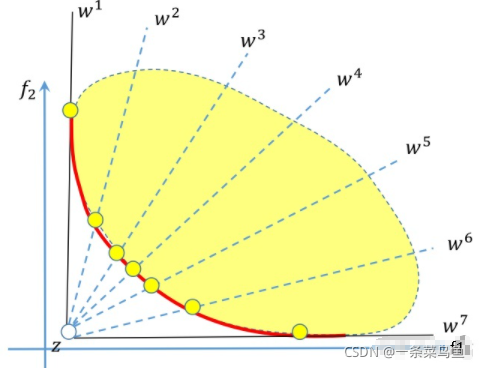
m a x 1 ≤ i ≤ m { λ ∣ f i ( x ) − z i ∗ ∣ } \mathop{max}\limits_{1\le i \le m} \{\lambda |f_i(x)-z^*_i|\} 1≤i≤mmax​{λ∣fi​(x)−zi∗​∣} 为所求的目标函数。 以目标函数中的一对值 ${\lambda }_1|f_1(x)-z_1^{\ast }|与{\lambda }_2|f_2(x)-z_2^{\ast }|$ 来说明, 根据需求我们需要求得两者之中的最大值。 但是为什么要求最大值呢? 我们看以下切比雪夫集合方法的表达式

m i n i m i z e    g t e ( x ∣ λ , z ∗ ) = m a x 1 ≤ i ≤ m { λ ∣ f i ( x ) − z i ∗ ∣ } minimize \ \ g^{te}(x|\lambda,z^*) = \mathop{max}\limits_{1\le i \le m} \{\lambda |f_i(x)-z^*_i|\} minimize  gte(x∣λ,z∗)=1≤i≤mmax​{λ∣fi​(x)−zi∗​∣}我们的需求是缩小 $g^{te}(x|\lambda ,z^{\ast })$ 的值以期获得约束集上的最小值。 这里我们考虑一个集合 A = { 10 , 8 , 7 , 4 , 5 } A = \{10,8,7,4,5\} A={10,8,7,4,5} , 我们获取了其中最大值 10 之后对其进行缩小, 来减小与理想值之间的差距 ( ${\lambda }_1|f_1(x)-z_1^{\ast }|$ 的几何意义也即 $f_1与Z_1^{\ast }之间的距离$ ) , 那么 10 在缩小之后顺带着带动了所有 < 10 的元素都进行了缩小。 这里的思想也就等价于不等式证明的思想, 证明函数小于某个确定值, 仅需证明其函数最大值小于该确定值即可。 因此, 如果集合中最大的值都达到了其最小值, 那么其他小于它的值肯定也达到了最小值。对于一个权重向量 $\lambda$ 是如此，每一个权重向量都是按照这个方式求得相应的解。

在切比雪夫聚合方法中, 一个确定点(个体) 移动方向可能是下图的情形。

---

1.3 边界交叉法 (Boundary Intersection Approach)

公式
$$\begin{gathered} minimize{g}^{bi}(x|\lambda ,z^{\ast })=d \\ subjectto{z}^{\ast }-F(x)=d\lambda x\in \Omega \end{gathered}$$

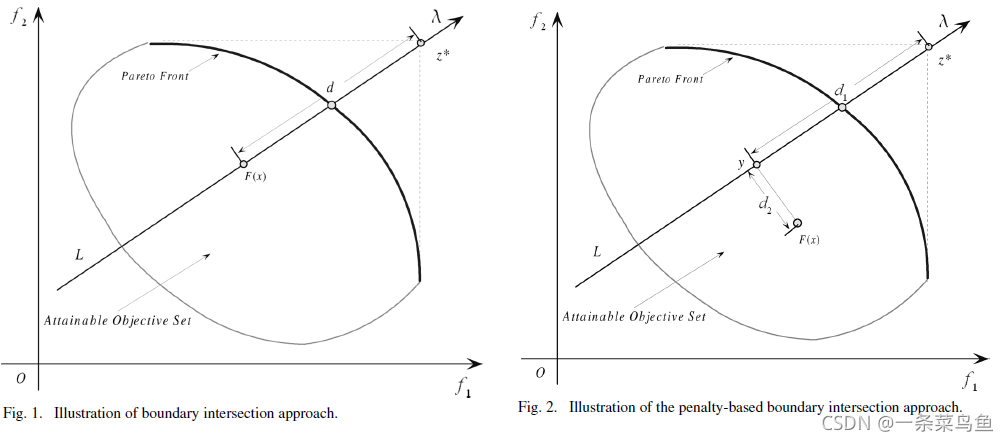
边界交叉法的核心思想在于缩短理想点 $z^{\ast }$ 与 实际点或者说个体 $M$ 之间的距离。

左图是基础边界交叉法的图示, 右图则是基于惩罚机制的边界交叉法图示。

见名知意, 基于惩罚机制的边界交叉法的精髓在于其加入了惩罚机制。 该惩罚机制在实际点距离理想点越远时惩罚力度越大(实质上也是迫使点更快趋近理想点), 与深度学习中的基于学习的SGD类似, 能够根据不同的实际情况来增大或缩小 LR。

---

2 算法流程

2.1 解的生成

公式
m i n i m i z e    g t e ( x ∣ λ , z ∗ ) = m a x 1 ≤ i ≤ m { λ ∣ f i ( x ) − z i ∗ ∣ } s . t . x ∈ Ω minimize \ \ g^{te}(x|\lambda,z^*) = \mathop{max}\limits_{1\le i \le m} \{\lambda |f_i(x)-z^*_i|\} \\ s.t. x\in \Omega minimize  gte(x∣λ,z∗)=1≤i≤mmax​{λ∣fi​(x)−zi∗​∣}s.t.x∈Ω

算法假设相邻的权重上的解相似，每个权重都有邻居。下面图中红色的点，它的邻居就是附近的四个点，用这四个点去生成新解。生成新解之后，就要替换邻域中的解了。这里面策略很多，可以随机替换邻域中两个解如果这个新解比他们好的话。如此，种群可以更新，最终收敛至近似的Pareto front。

---

2.2 输入

1. 多目标优化问题
2. 算法终止条件
3. N: MOEA/D 定义的种群大小
4. 均匀分布的 N 个权重向量: ${\lambda }_1,...,{\lambda }_n$
5. T: 每个邻域中权重向量的个数 (圈的大小)

---

2.3 初始化

• Step 1

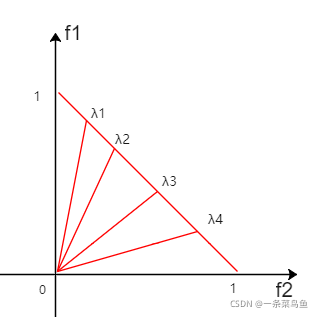
  计算每个权重向量之间的欧式距离 (对于二目标优化就是 $(x_1,y_1)与(x_2,y_2)$ 的距离)，对于每个权重向量 ${\lambda }^i$ 得到离它最近的 $T$ 个权重向量存放于 $B(i)$（相邻集合）中。实质上, 如果 ${\lambda }^i与{\lambda }^j$ 的距离近, 其对应的 $g^{te}(x|{\lambda }^i,z^{\ast })与g^{te}(x|{\lambda }^j,z^{\ast })$ 也相近 。如下图所示, 由于 ${\sum }_{i=0}^m{\lambda }^i=1$ , 因此所有的 $\lambda$ 会落在一条直线上, 故欧式距离越小，表示越相邻；

• Step 2

  随机生成种群 $x_1,x_2,...,x_n$

• Step 3

  初始化 $z^{\ast }=(z_1^{\ast },z_2^{\ast },...,z_m^{\ast })$ , z i = m i n { f i ( x 1 ) , f i ( x 2 ) , . . . , f i ( x N ) } z_i = min\{f_i(x_1),f_i(x_2),...,f_i(x_N)\} zi​=min{fi​(x1​),fi​(x2​),...,fi​(xN​)} 即目标函数上的最小值

• Step 4

  创建外部种群 EP 用于存储精英个体, 也即非支配个体, 初始为空

---

2.4 种群更新

参数解释

$EPElitepopulation精英种群$

$B(i)邻近集合-距离x最近的T个权重向量$

$z^{\ast }理想值$

$F{V}^{x(i)}FunctionValue目标函数值$

$g^{te}(x(i)|\lambda ,z^{\ast })理解为到Z^{\ast }点的距离$

算法步骤

对每个编号为 i 个体执行以下操作

• Step 1

  从邻近集合 $B(i)$ 中随机选取序号 $k,l$ 利用基因交叉生成新个体 $y$

• Step 2

  对生成的新解(个体)进行修复和改进产生 修复后的解 $y^{\prime }$

  notes: 修复的意义在于有时生成的解并不符合约束条件, 这时就需要执行修复函数进行修复,使其符合约束

• Step 3

  更新理想值 $z^{\ast }$ , 判断新生成的 $y^{\prime }$ 是否优于 $z^{\ast }$, 优于则替换

• Step 4

  更新邻近集合 $B(i)$ , 如果领域中解 $g^{te}(x(i)|\lambda ,z^{\ast })$ 小于 $g^{te}(y^{\prime }|\lambda ,z^{\ast })$ , 则更新解对应的函数值 $F{V}^{x(i)}=F{V}^{y^{\prime }},x(i)=y^{\prime }$

• Step 5

  更新精英种群 $EP$, 从 $EP$ 中移除所有被 $y^{\prime }$ 支配的解, 如果不存在则将 $y^{\prime }$ 加入 $EP$ 集

• 终止条件 是否达到迭代次数, 否则继续执行更新操作

---

2.5 算法框架

---

2.6 动画演示

动画制作比较简陋, 但大致的逻辑是对的, 可以参考, 后面有时间再做修改, 请不要做丑拒的小盆友~

更新后的 GIF 演示

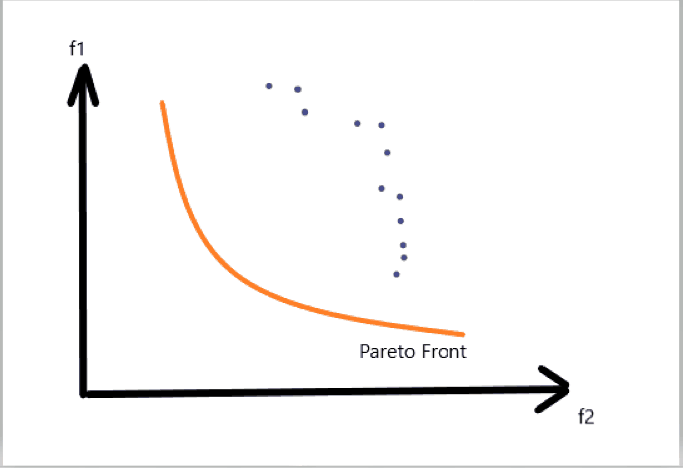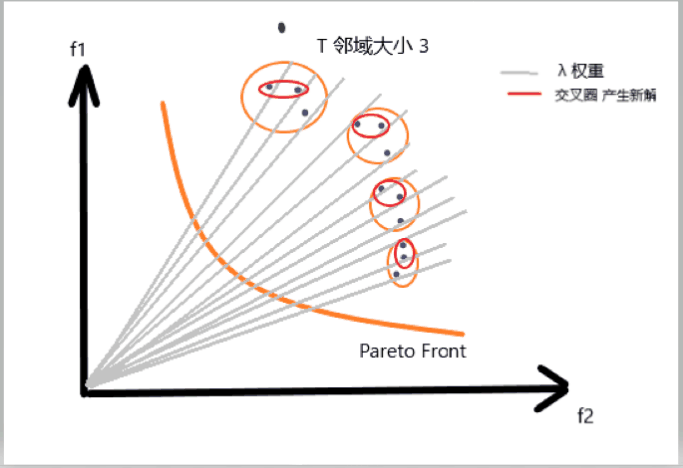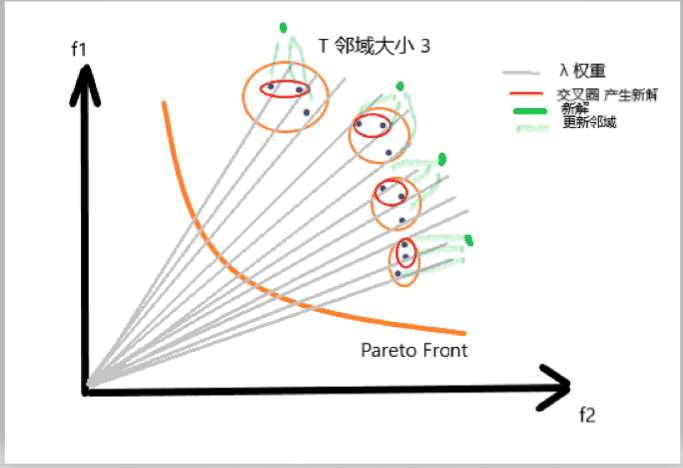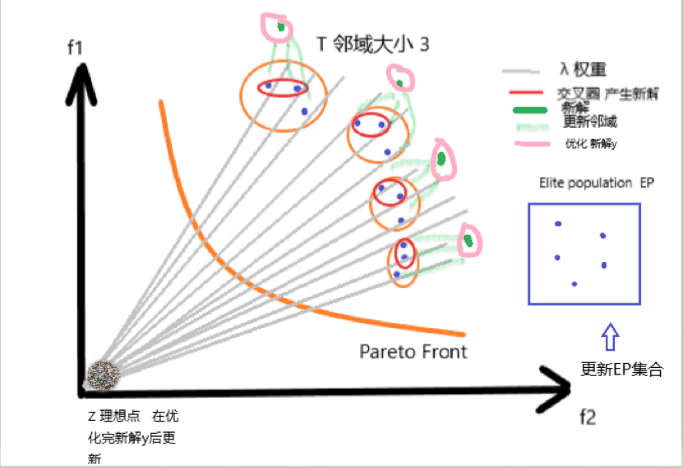
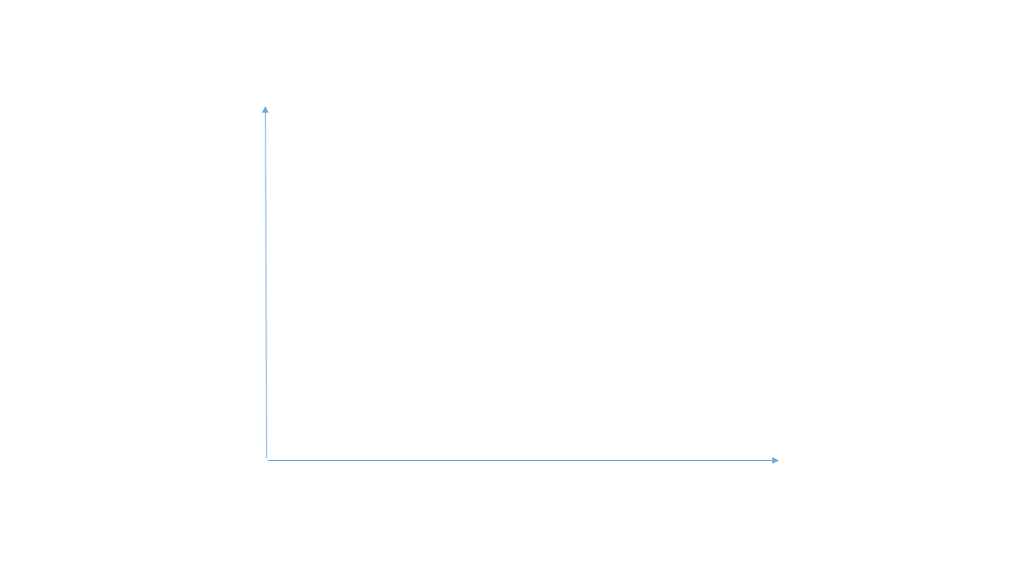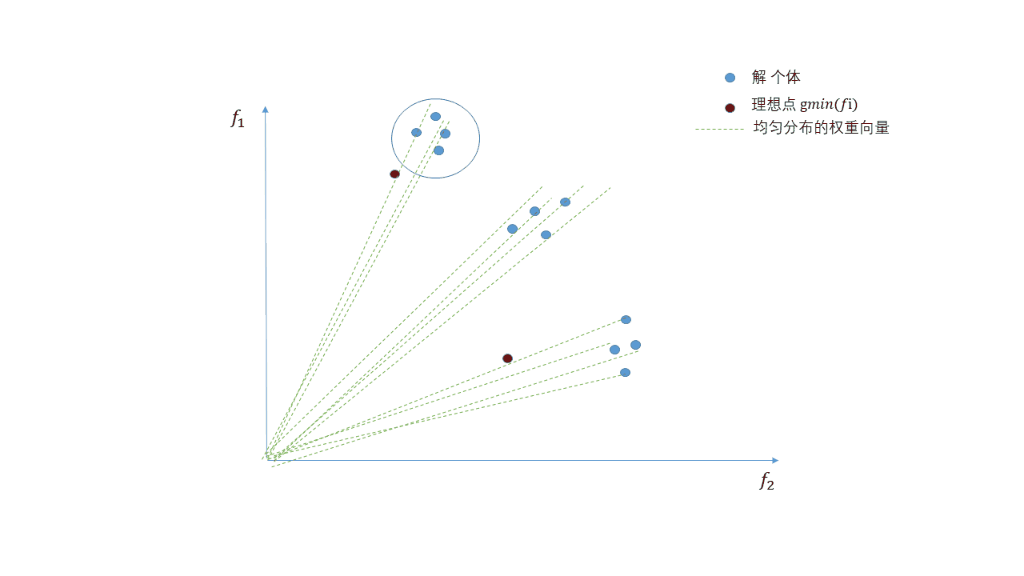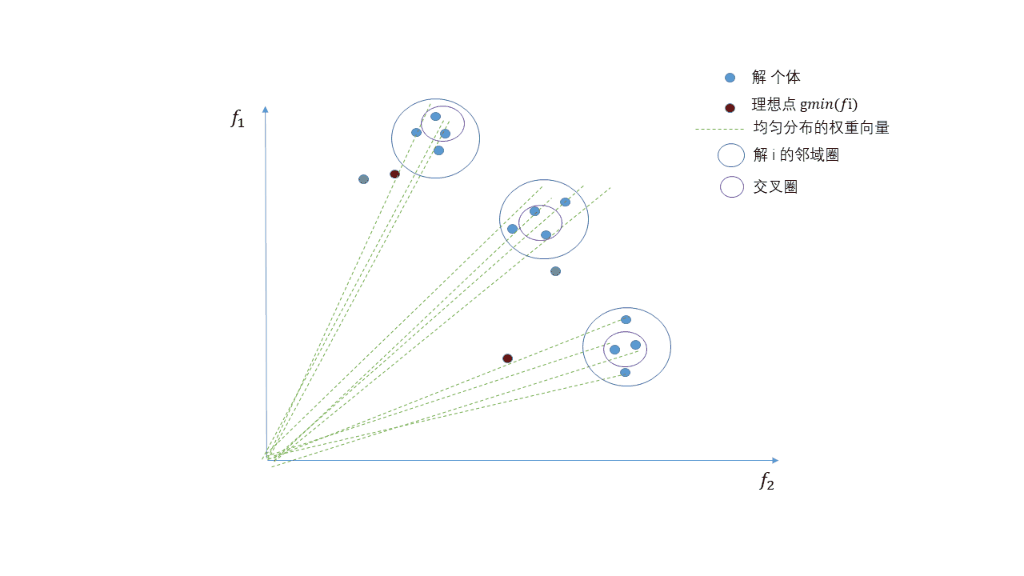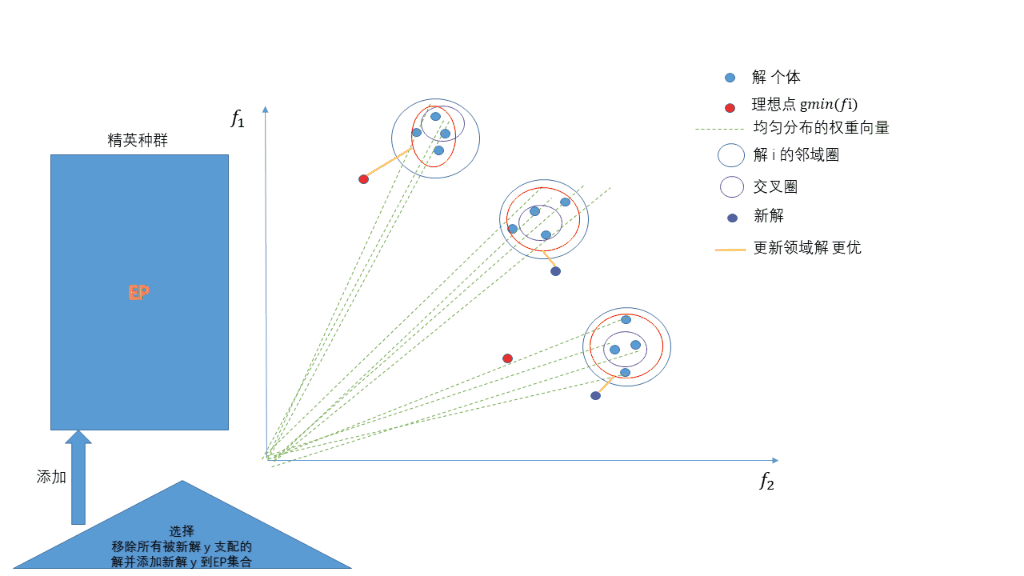
附一个讲的很好的知乎回答 respect link.