时序数据相似度距离衡量- DTW距离

DTW (Dynamic Distace Warpping) 距离

传统基于范数距离 （e…g, 欧式距离，曼哈顿距离） 的序列相似度比较面临两个很大的问题：

• 不能处理两个长度不一的序列
• 会产生local time shifting问题， 即由于序列的采样率不同或序列的产生频率不同，两条意义相同的序列可能会有很大的范数距离。这是由于在此方法下，序列只能够一一匹配。
• 比如两条语音数据说同一句话 （我爱你)，voice1 = [（我，t1), (我，t2), (爱，t3), (你， t4)], voice2 = [（我，t1), (爱，t2), (爱，t3), (你， t4)], 由于采样率不同，如果采用点对点的一一匹配显然会计算出这两条序列的距离较大。 假设编码voice1= 1123, 编码voice2=1223, 距离为1.但其实这两条序列距离为0， 因为它们表达的是同一个语义。在轨迹序列中如果使用传统的一一匹配，也会存在这样的问题。

因此，DTW提出用于解决local time shift的问题。它的基本思想是 两条序列可以进行多对一的匹配。或者说，一对多的匹配。

DTW简介

DTW的应用主要是为了解决语音识别领域中语速不同的情况下如何计算距离相似度的问题。
DTW的动态迭代如下：

具体实现，以上述的（1123）和（1223）为例子，先计算两点间的距离矩阵 （这里用曼哈顿距离）

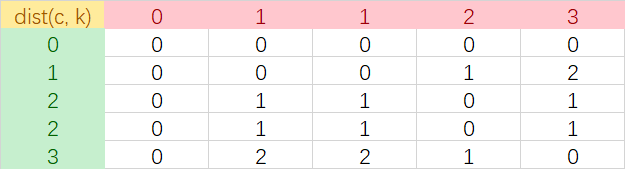
接着，找一条从（0，0)到（4，3）的最短路径，最短路径值即为DTW距离。但是公式里面要求如果斜着，则需要认为是走了两步，这也是合理的。使用动态规划查找最短路径过程如下：

Java实现DTW距离

package precomputation;

import java.util.Arrays;

public class DTW {
	
	public static void main(String[] args) {
		int[] seq1 = {1,1,2,3};
		int[] seq2 = {1,2,2,3};
		int[][] res = DTW(seq2,seq1);
		System.out.println(Arrays.deepToString(res));
		}
	
	
	public static  int[][] DTW(int[] seq1, int[] seq2)
	{
		int m = seq1.length;
		int n = seq2.length;
		
		int[][] dists = new int[m][n];
		int[][] dp = new int[m][n];
		for(int i=0;i<m;i++)
		{
			for(int j=0;j<n;j++)
			{
				dists[i][j] = Math.abs(seq1[i]-seq2[j]);
			}
		}
		// 初始化dp的第一行和第一列
		dp[0][0] = dists[0][0];
		for(int i=1;i<m;i++)
		{
			dp[i][0] = dp[i-1][0]+dists[i][0];
		}
		for(int j=1;j<n;j++)
		{
			dp[0][j] = dp[0][j-1]+dists[0][j];
		}
		for(int i=1;i<m;i++)
		{
			for(int j=1;j<n;j++)
			{
				dp[i][j] = Math.min(Math.min(dp[i-1][j-1]+2*dists[i][j],dp[i-1][j]+dists[i][j]), dp[i][j-1]+dists[i][j]);
			}
		}
		return dp;
	}
}

其他语言实现

http://www.cnblogs.com/ChengQH/p/2dc8272d6b045b9cee3a02d221662251.html
http://www.cnblogs.com/tornadomeet/archive/2012/03/23/2413363.html
https://www.cnblogs.com/ningjing213/p/10502519.html

Distance/Similarity Measures

• DISSIM: Dissimilarity distance function.
o Frentzos, Elias, Kostas Gratsias, and Yannis Theodoridis. “Index-based most similar trajectory search.”, ICDE 2007.
• DTW: Dynamic Time Warping for time series.
o Yi, B-K and Jagadish, HV and Faloutsos, Christos. “Efficient retrieval of similar time sequences under time warping”. In ICDE (1998).
o Keogh, Eamonn J and Pazzani, Michael J. “Scaling up dynamic time warping for datamining applications.” In ACM SIGKDD (2000).
o Keogh, Eamonn, and Chotirat Ann Ratanamahatana. “Exact indexing of dynamic time warping.” In Knowledge and information systems (2005).
• EDC: Euclidean Distance for 2D Point Series (Trajectories).
• EDR: Edit Distance on Real sequences.
o Chen, Lei, M. Tamer Özsu, and Vincent Oria. “Robust and fast similarity search for moving object trajectories.” In. ACM SIGMOD, 2005.
• EDwP: Edit Distance with Projections.
o Ranu, Sayan, P. Deepak, Aditya D. Telang, Prasad Deshpande, and Sriram Raghavan. “Indexing and matching trajectories under inconsistent sampling rates.”, ICDE, 2015.
• ERP: Edit distance with Real Penalty.
o Chen, Lei, and Raymond Ng. “On the marriage of lp-norms and edit distance.” In. VLDB Endowment, 2004.
• Frechet: Trajectory Distance measure.
o Buchin, Kevin, Maike Buchin, and Yusu Wang. “Exact algorithms for partial curve matching via the Fréchet distance.” In. ACM-SIAM, 2009.
o Alt, Helmut, and Michael Godau. “Computing the Fréchet distance between two polygonal curves.” International Journal of Computational Geometry & Application, 1995.
• LCSS: Largest Common Subsequence distance.
o Vlachos, Michail, George Kollios, and Dimitrios Gunopulos. “Discovering similar multidimensional trajectories.” ICDE, 2002.
• LIP: Locality In-between Polylines - trajectory distance measure.
o Pelekis, Nikos, Ioannis Kopanakis, Gerasimos Marketos, Irene Ntoutsi, Gennady Andrienko, and Yannis Theodoridis. “Similarity search in trajectory databases.” In IEEE International Symposium on Temporal Representation and Reasoning, 2007.
• OWD: One Way Distance trajectory distance measure.
o Lin, Bin, and Jianwen Su. “Shapes based trajectory queries for moving objects.” In ACM international workshop on Geographic information systems, 2005.
• PDTW: Trajectory distance measure.
o Keogh, Eamonn J., and Michael J. Pazzani. “Scaling up dynamic time warping for datamining applications.” In ACM SIGKDD, 2000.
• STED: Spatial-Temporal Edit Distance.
o Yuan, Yihong, and Martin Raubal. “Measuring similarity of mobile phone user trajectories – a Spatio-temporal Edit Distance method.” In International Journal of Geographical Information Science, 2014.
• STLCSS: Spatial-Temporal Largest Common Subsequence distance.
o Vlachos, Michail, Dimitrios Gunopulos, and George Kollios. “Robust similarity measures for mobile object trajectories.” In IEEE Database and Expert Systems Applications, 2002.
• STLIP: Spatial-Temporal Locality In-between Polylines.
o Pelekis, Nikos, Ioannis Kopanakis, Gerasimos Marketos, Irene Ntoutsi, Gennady Andrienko, and Yannis Theodoridis. “Similarity search in trajectory databases.” In IEEE International Symposium on Temporal Representation and Reasoning, 2007.
• TID: Transformation Innovation Distance.

Github python package

常见的轨迹相似度距离度量