目录
第一节 认识复杂度、对数器、二分法与异或运算
1. 认识复杂度
2. 对数器
-

-
对数器的实现方法:

-
JAVA随机整数生成:

3. 二分法
-
复杂度为
logn。 -
认识二分:

-
二分法中,为了安全,mid的下标最好用减法算出,以免加法溢出。位运算更快
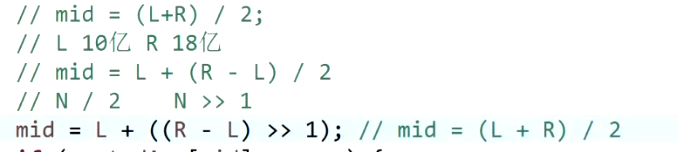
-
常见的一些位运算写法:
x^2 == x << 1; x^2 + 1 == x << 1 | 1; x/2 == x >> 1; -
一个有序数组中,找某个数是否存在:

-
在一个有序数组中,找>=某个数最左侧的位置:

-
在一个有序数组中,找<=某个数的最右边位置:

-
局部最小值问题:(不一定是有序才可以二分的,具有排它性就可以二分)
一个数组中,小于m的数都在左边,大于m的数都在右边,找出最右边的一个小于m的数。(具有排他性)
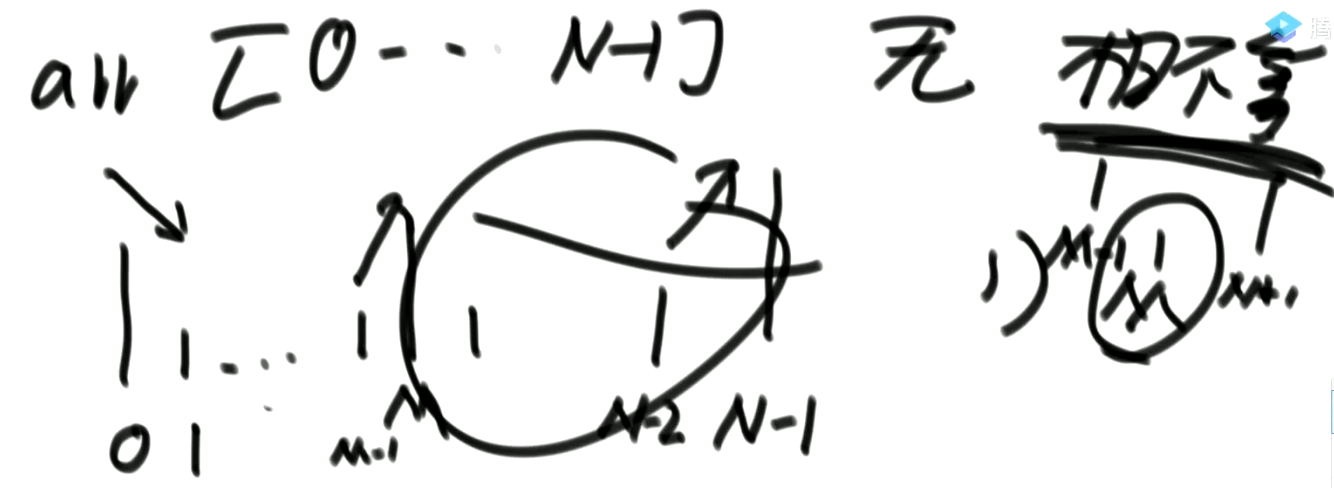
只要在解决问题的过程中,可以构建出排他性,就可以使用二分。
4. 异或运算
-

-
交换a,b:
a = a ^ b b = a ^ b a = a ^ b -
数组中,只有一种数,出现次数是奇数,找出这个数:

原理:0与任何数异或等于其本身,两个相同的数异或等于0.
-
提取一个整数最右侧的1,其他位置变为0:
N = N & ((~N)+1) -
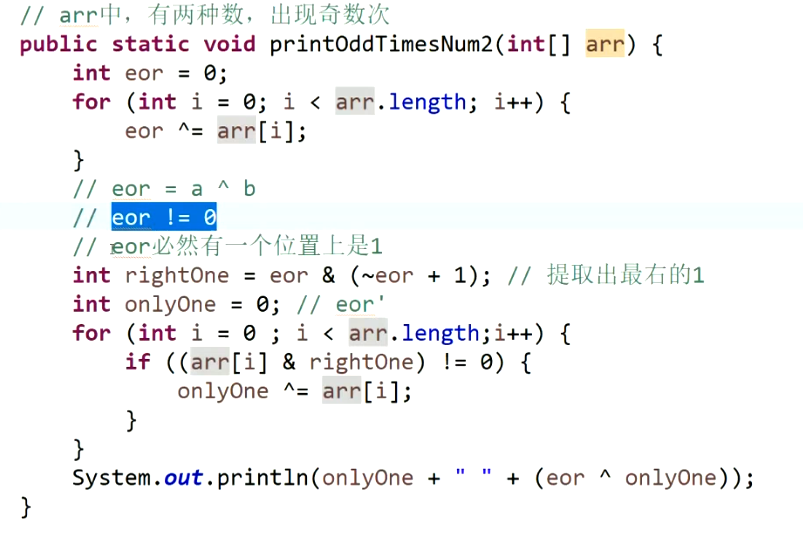
一个数组中,有两种数出现了奇数次,其它数都出现了偶数次,怎么找到并打印这两种数。
第二节 链表、栈、队列、递归行为、哈希表和有序表(JAVA)
1. 链表、栈、队列
-
Java中定义链表:


-
反转单向链表:

-
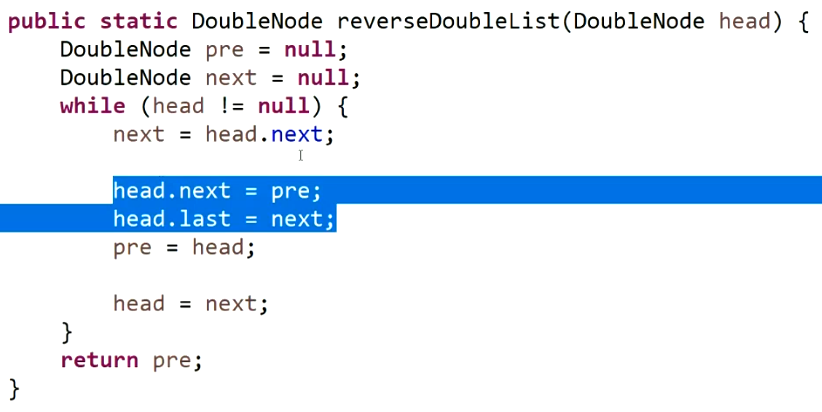
反转双向链表:
-
删除链表中指定值的所有节点:
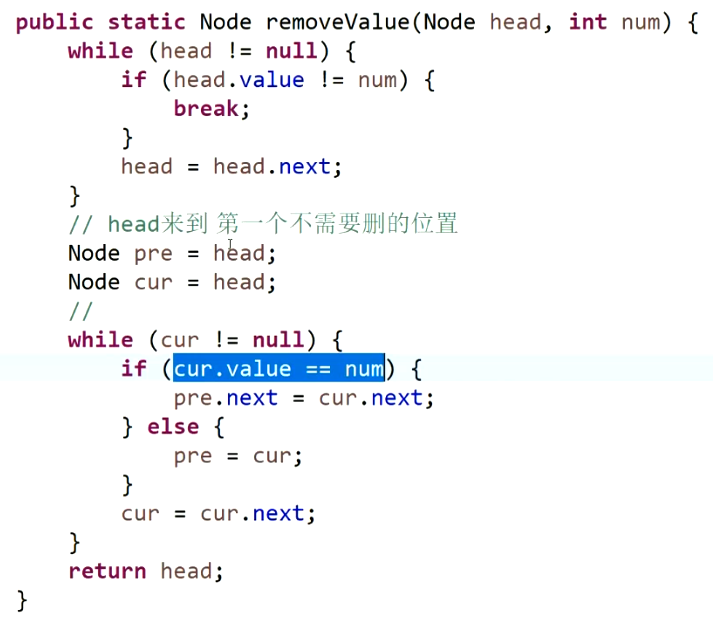
指定的值很有可能在链表头部,所以需要先找到第一个不为值的节点,记为最后要返回的头节点。 -
实现一个自定义栈,使得压入栈、得到栈顶元素、获取当前栈的最小元素这三个操作的时间复杂度都为O(1):
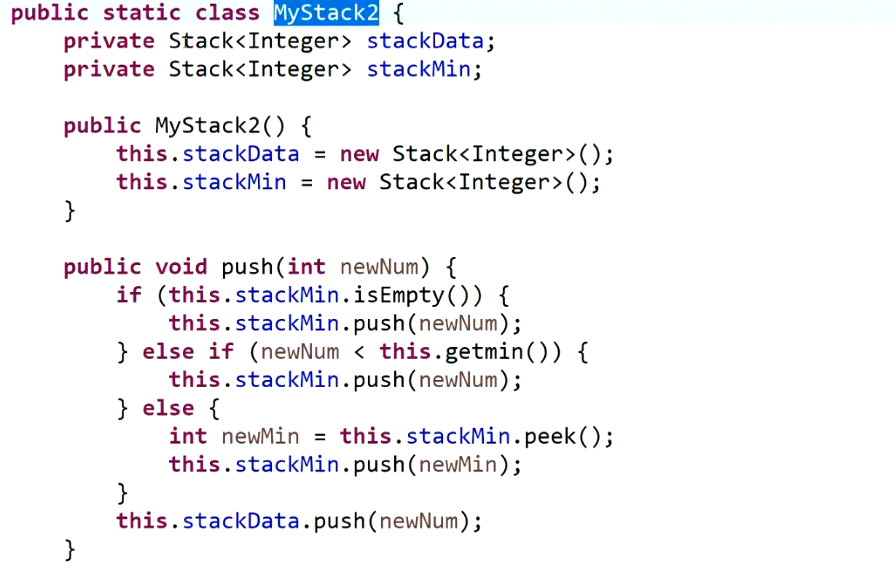
思路两个:
-
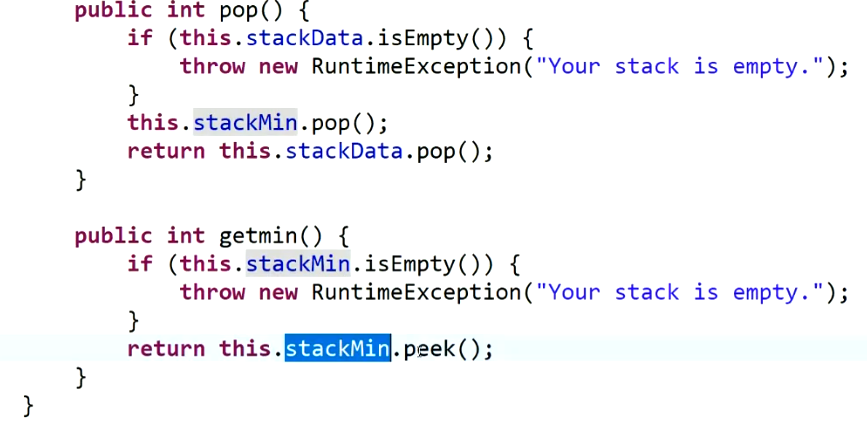
通过两个栈结构实现:一个栈用于保存数据,一个栈用于保存当前最小值;每次压入一个元素,就判断进栈数据与最小值栈顶数据的大小,更小的压入最小栈中,数据正常进栈;取数据时,最小栈需要同步弹出,但不需要返回;拿最小值时,返回最小栈栈顶元素。
-
也通过两个栈实现:一个存数据,一个存最小值,只有在进栈数据小于等于最小栈栈顶时,将数据压入最小栈。弹出时,最小栈元素与数据栈相同就弹出,不同就不弹出。省空间
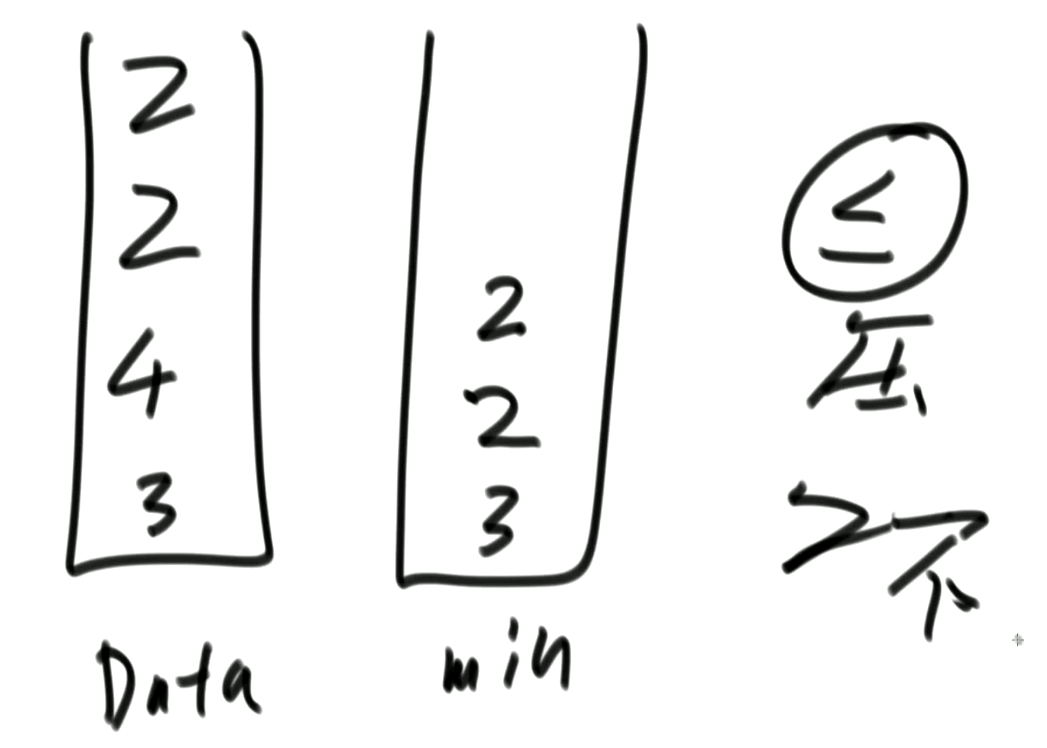
-
用两个栈实现一个队列:
一个push栈,一个pop栈,用户压入数据全部放入push栈;用户导出数据,先把push栈倒置数据到pop栈,然后取pop栈栈顶元素。需要注意的是,任何时候用户要取数据的时候,要先判断pop栈是否为空,只有pop栈为空的时候,才能将push栈的数据加入到pop栈中,否则只有压入到push栈中。
2. 递归行为
有一类递归算法的时间复杂度是可以分析的:
前提是,递归过程中子问题规模一致(规模为N/b)。时间复杂度将满足:
T(N) = a * T(N/b) + O(Nd)
每个子问题的规模为N/b,在子问题规模等量小的情况下,每个子问题调用了a次;除去子问题调用之外的时间复杂度为O(Nd)。
只要满足这样形式的递归(子问题规模一致),都可以使用这个公式计算时间复杂度。
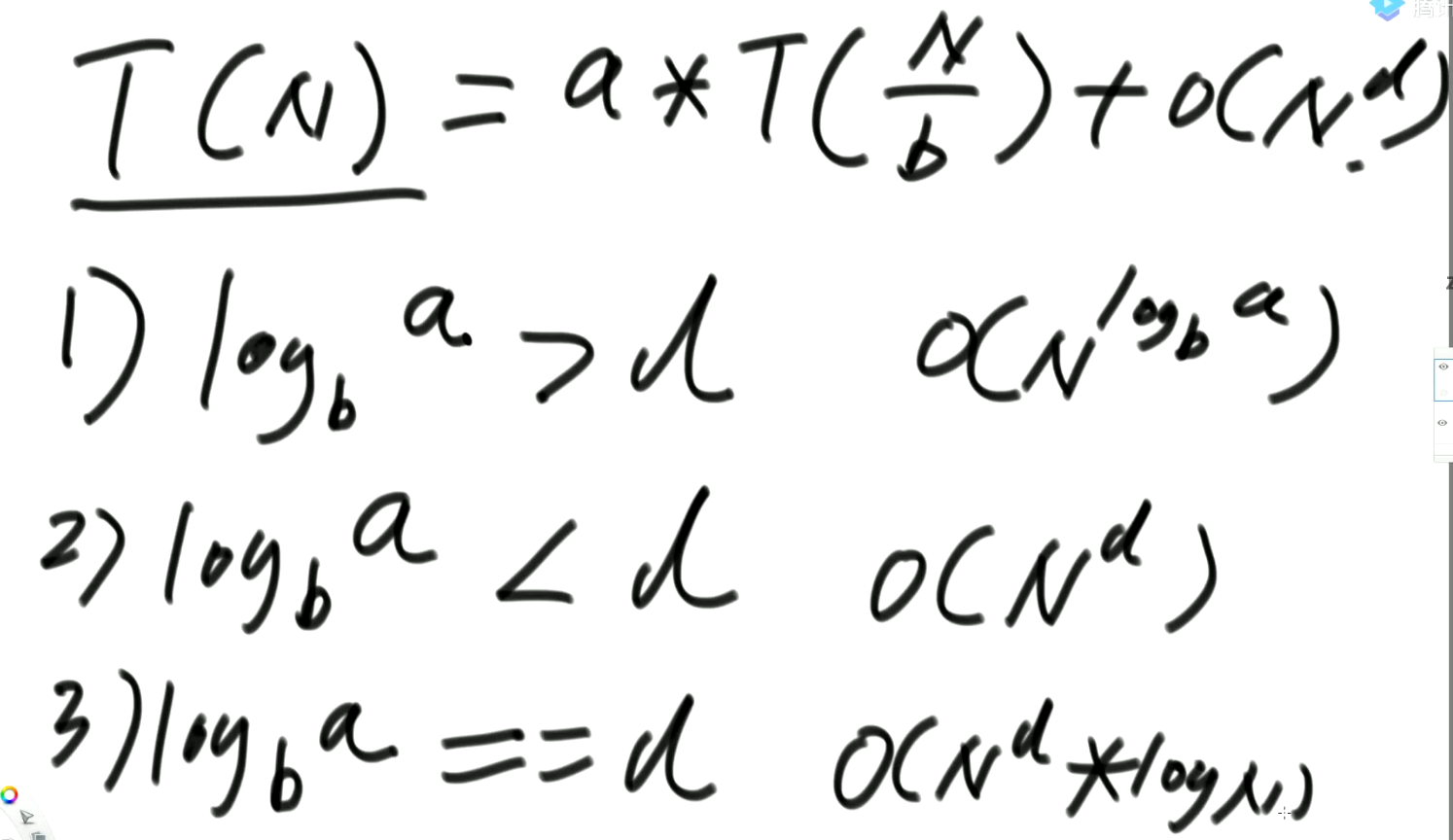
上图1,2,3是时间复杂度对应的化简结果,背就完事了。

3. 哈希表、哈希集
-
JAVA写算法常用的哈希表的用法:
常用实现类
HashMap<T,T>put(key,value):添加键值对,当Map中不存在指定key时,就是新建操作,存在指定key时就是更新操作。containsKey(key):检查某个键是否存在get(key):获取键对应的值remove(key):删除指定键对应的键值对
-
会用哈希表,也就会用哈希集
HashSet。在JAVA底层哈希集的实现与哈希表的实现是一样的,只是它不带value值。add(key):添加一个值到Set中contains(key):判断某个值是否存在Set中remove(key):删除指定的值
-
哈希表在使用时,增、删、改、查,时间复杂度皆为O(1)
-
哈希表键值的引用传递与值传递:其实就和基本类型与引用类型是一个道理。基本类型按值传递,值不一样对应不一样的key;引用类型按引用传递,引用一样,则只对应一个key。
对应键值对也是同样的道理:键值对为基本类型时,哈希表会采用值传递,会占用新的内存空间去存键和值;当键值对为引用类型时,哈希表采用引用传递建立,只会存键和值的引用地址。
特例是String类型,这个类型在键值对的构造中按值传递。
4. JAVA中的有序表TreeMap
- 有序表
TreeMap的所有操作:增、删、改、查操作的时间复杂度都是O(logN); - 哈希表能使用的操作,有序表都可以使用,除此之外,它还支持:
firstKey():返回最小的键;lastKey():返回最大的键;floorKey(key):返回小于等于key的最近一个key;ceilingKey(key):返回大于等于key的最近一个key;
- 有序表底层可以使用AVL树、红黑树、SB树实现。
- 有序表的键必须是实现
Comparator接口的对象。即必须是实现了比较器的对象。
第三节 归并与随机快排
1. 归并排序以及分治思想
-
归并排序:
O(NlogN)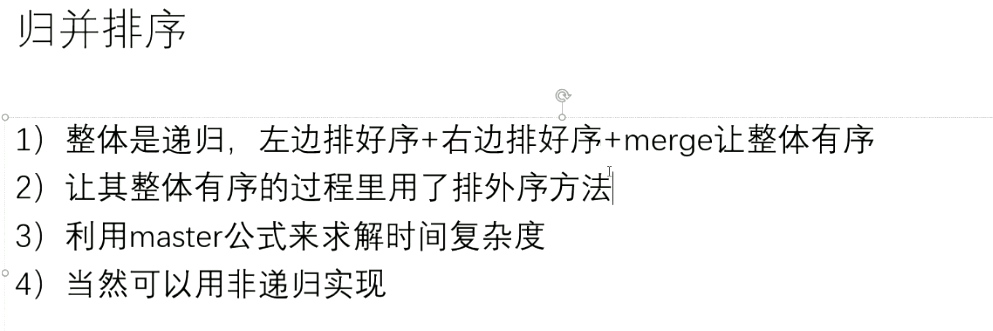
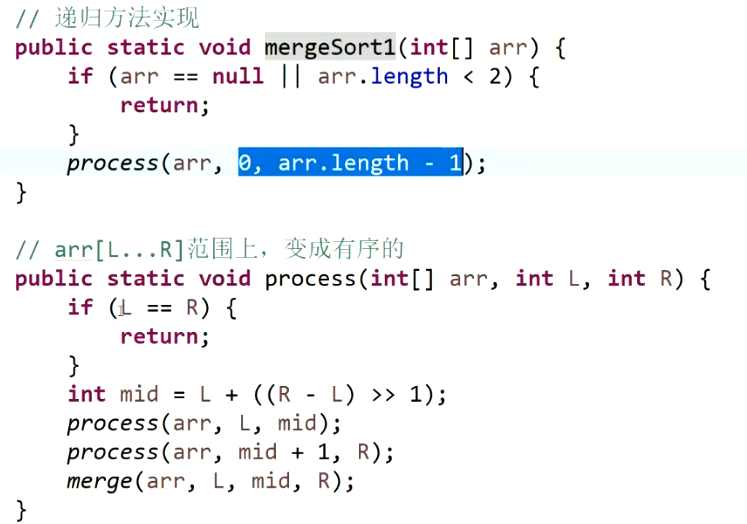

归并排序非递归的实现:
O(NlogN)
mergeSize定义当前有序的左组长度。 -
归并排序的精髓,用一道题理解:【小序对】

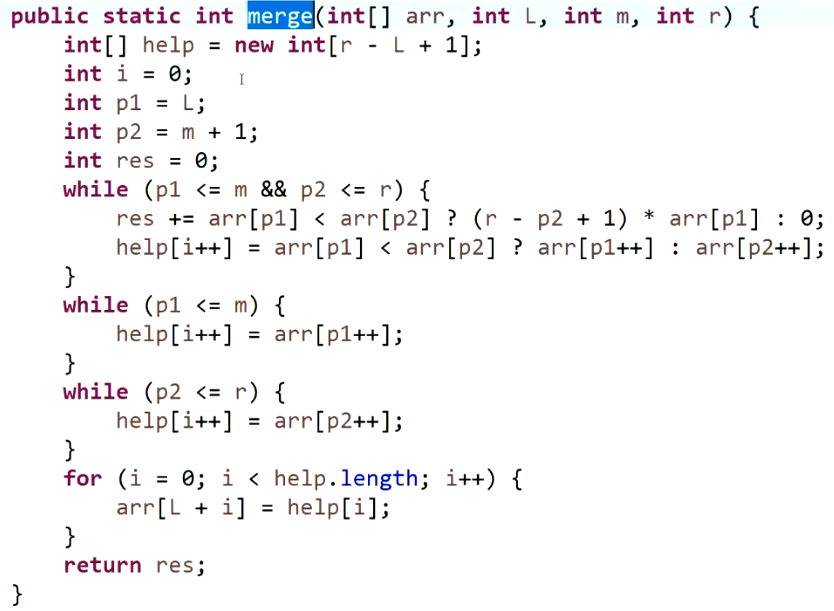
这道题可以用归并排序。算法流程:将数组通过归并操作来判断是否产生小和。归并
merge操作时,左组的数小于右组的数就会产生小和,而判断右组有多少个数大于左组的数只需要通过下标相减就可以得到(左组与右组进行merge时都是有序的);左组的数大于等于右组时,右组的数先合并,再合并左组的数,此时不产生小和。思想:每一次的归并,就是在已知一个左组(有序)的情况下,去找一个更大的右组(有序),然后站在右组的基础上去找左组有多少个数小于右组的元素(归并过程实现)。求完小和之后,将左右两组合并成左组使其有序,等待下一次合并。因此,算法的正确性可以得到验证。

-
另外一个题加深对归并思想的理解:
求数组的逆序对,对于给定数组,求出能够产生多少个逆序对。对于当前位置的元素,如果其后有元素小于当前元素就可以产生一个降序对。求每一个小的集合,左边的数有多少比右边大
private static int merge2(int[] arr, int l, int mid, int r) { int ans = 0, pos = 0,p1 = l, p2 = mid+1; int[] help = new int[r - l + 1]; while(p1 <= mid && p2 <= r) { if(arr[p1] > arr[p2]) { ans += r-p2+1; help[pos++] = arr[p1++]; }else { help[pos++] = arr[p2++]; } } while(p1 <= mid) { help[pos++] = arr[p1++]; } while(p2 <= r) { help[pos++] = arr[p2++]; } for(int i = 0;i < help.length;i++) { arr[l+i] = help[i]; } return ans; }思想:求逆序对
题目时要求左边的数比右边对少数大,可以采用归并排序。
- 将数组不断分为左组和右组,然后对左组和右组进行归并操作;
- 归并时,左组和右组分别是有序的(归并的过程中已经排好序,在该问题中是逆序,只是这些有序的数不会离开他们上一层的左组和右组的范围)。
- 如果左组的数大于右组的数,那么直接合并左组的数(逆序),并且此时可以生成的逆序对是
r-p2+1个,因为右组的所有其它数,在逆序的情况下都比这个数小。 - 如果左组的数小于等于右组的数,那么合并右组的数。
-
什么时候可以用归并排序的思想——分治:题目中要求数组左侧或右侧有数比它小,或者比它大的数有多少对时。可以采用归并,只要在
merge过程中,归并统计即可。归并排序的核心就是:每一次排序都没有浪费结果的有序性,可以在下一次归并的时候继续使用。所以大大提升了效率。
-
总结,在使用归并排序的过程去解决问题时,如果要求左侧多少数小于右侧,那么需要按升序进行归并;否则按照降序进行归并。
2. 快速排序以及随机快排
-
荷兰国旗问题:以arr[R]做划分值,返回数组中等于arr[R]的下标范围。(指的就是partition划分的过程)

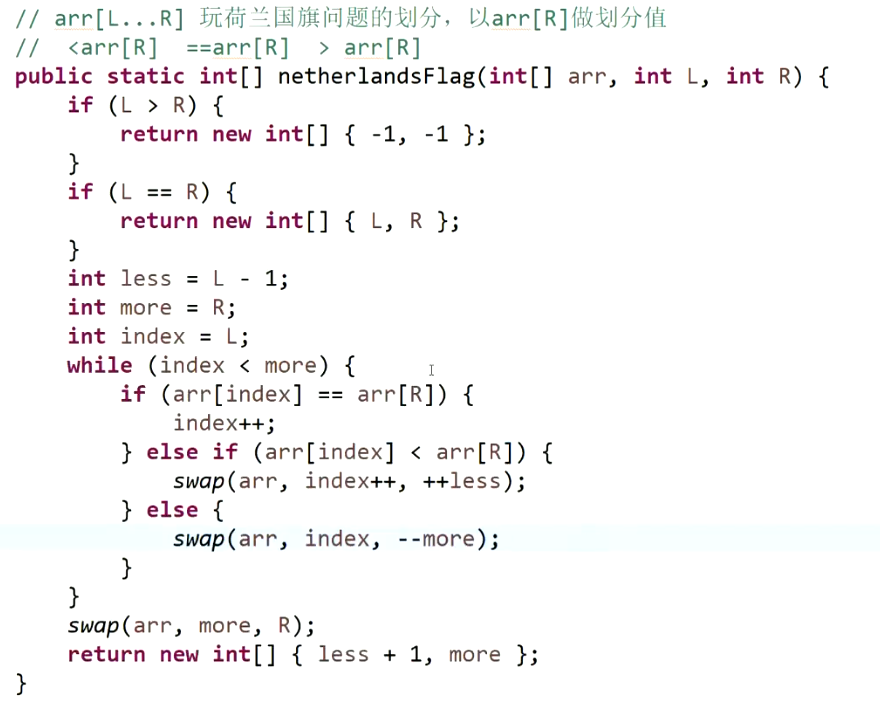
-
快排1.0的实现:以arr[R]最为划分值,每次与划分值相等的将会放在左边。
O(N^2^)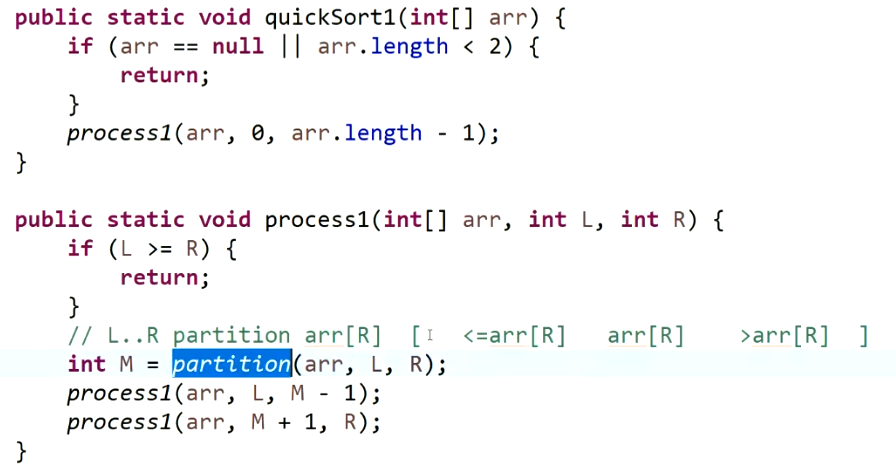
-
快排2.0的实现(以arr[R]作为划分值):一次将相等的一批数放在中间,基于荷兰国旗问题。
O(N^2^)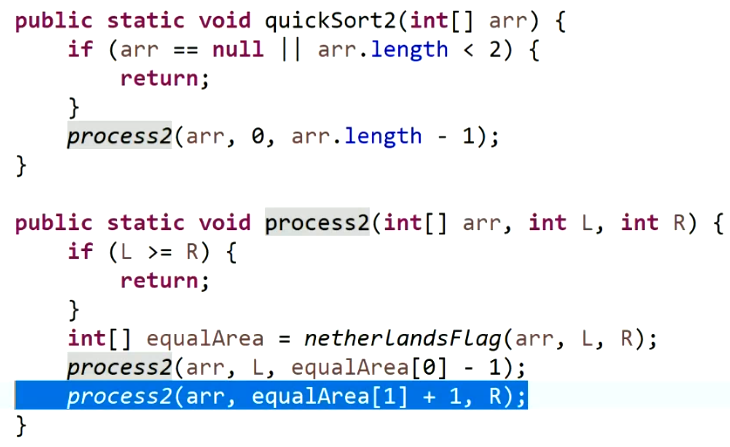
-
快排3.0的实现:随机选一个数作为划分值,以及加上荷兰国旗问题的优化,复杂度为
O(NlogN)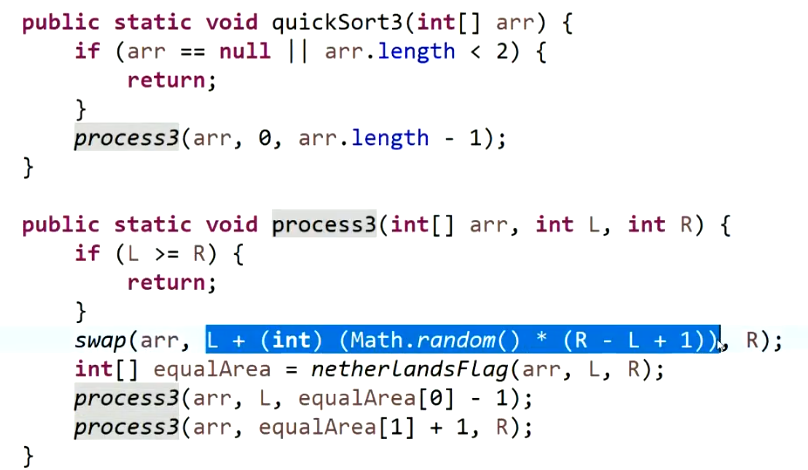
第四节 比较器与堆
1. 堆结构

关于从上往下以及重下往上建堆效率的问题:

2. 堆的使用
-
JAVA工具类中实现的堆结构
PriorityQueue<E>,常用的方法有,默认的比较器实现的是小根堆。add(E)clear():清除优先队列中所有元素contains(value):检查指定值是否存在于优先队列中peek():获取队列头元素,但不删除poll():获取并删除队列头元素
-
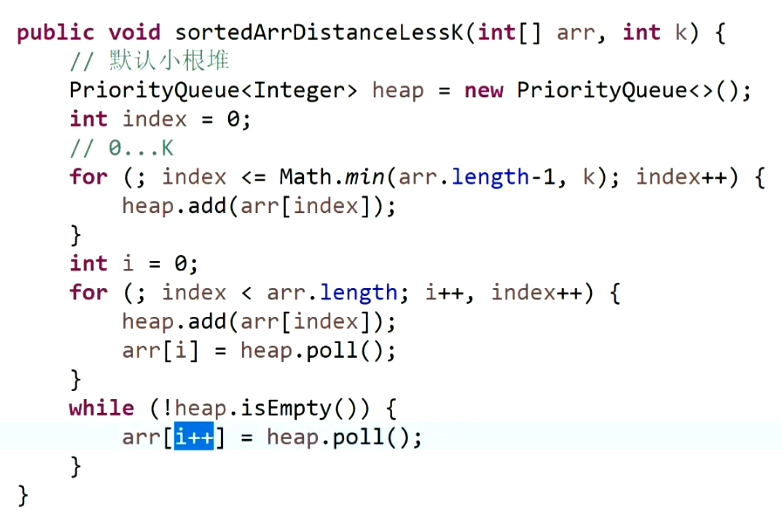
与堆相关的题目:

思路:将前k+1个数放入小顶堆,取出堆顶元素放入第一个位置,然后后面依次重复,即可排好。
-
不要试图通过额外的引用,改变
PriorityQueue中元素的值,堆将不会动态的保证队列中的有序性。
3. 比较器

-
任何比较器遵循的规则
int comp(T obj1, T obj2)返回-1或负数的情况,就是排序中要将obj1排在前面的情况;
返回1或正数的情况,就是排序中将obj2排在前面的情况;
返回0的情况,就是obj1与obj2相等。
-
通过比较器构造一个大根堆:
PriorityQueue<Integer> queue = new PriorityQueue<>( (x, y)->{ return y - x; } );
第五节 Trie、桶排序、排序总结
1. trie(前缀树)

例子:
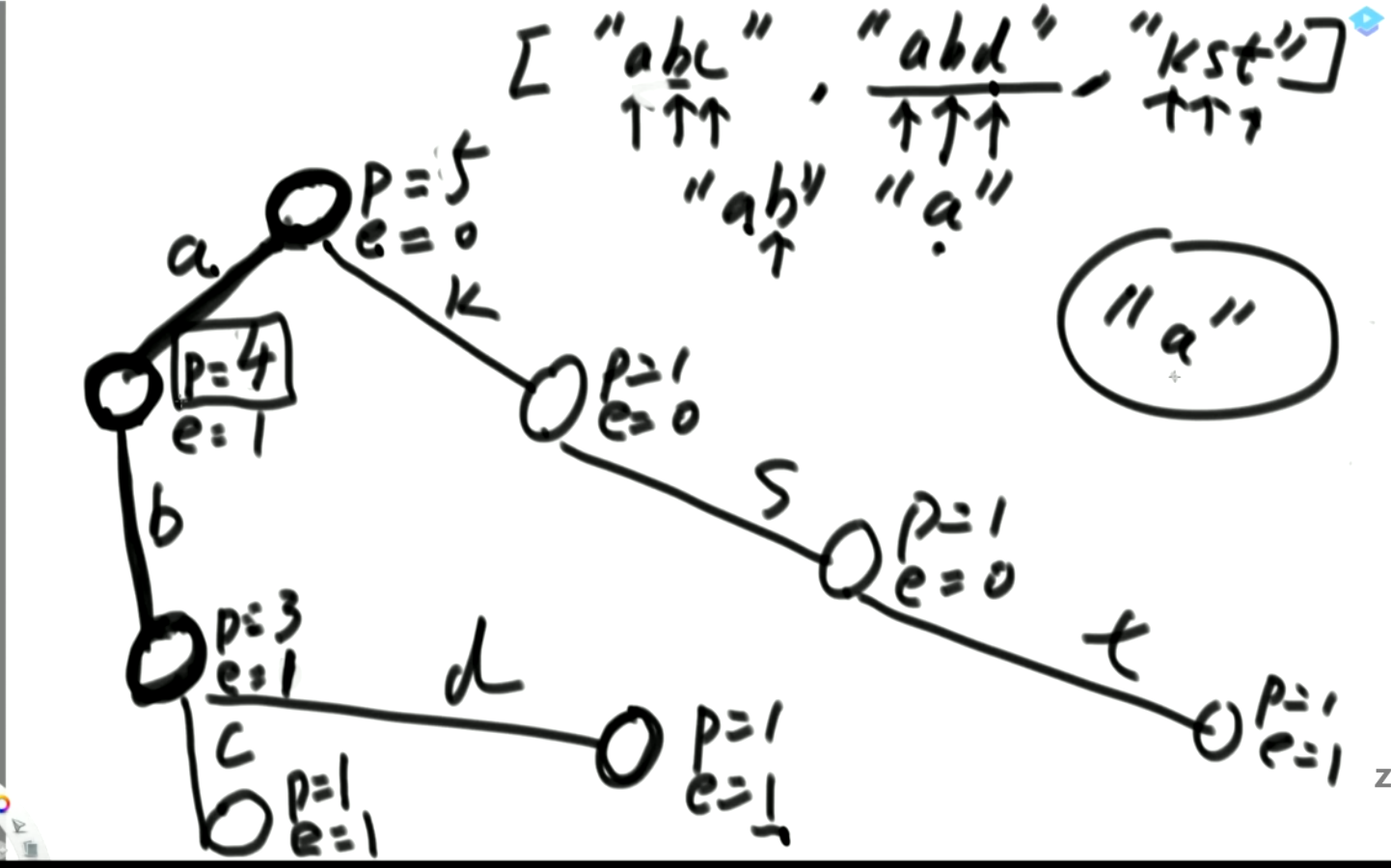
可以进行的查询:前缀树的构建,目的就是为了方便查询
- 指定某个字符串加入了多少个,从根节点遍历,直到最后一个字符,检查end值为多少即可。
- 以某个字符为前缀的字符串有多少个,从根节点遍历完,直到最后一个字符结点,检查pass值即可。
实现:方法1:只能适用于字符全是小写,内部每个结点使用一个Node[26]的数组保存分支。
public static class Node1 {
public int pass;
public int end;
public Node1[] nexts;
public Node1() {
pass = 0;
end = 0;
// 0 a
// 1 b
// 2 c
// .. ..
// 25 z
// nexts[i] == null 第i个字符没有经过
// nexts[i] != null 第i和字符经过了
nexts = new Node1[26];
}
}
public static class Trie1 {
private Node1 root;
public Trie1() {
root = new Node1();
}
public void insert(String word) {
if (word == null) {
return;
}
char[] str = word.toCharArray();
Node1 node = root;
node.pass++;
int path = 0;
for (int i = 0; i < str.length; i++) { // 浠庡乏寰�鍙抽亶鍘嗗瓧绗�
path = str[i] - 'a'; // 鐢卞瓧绗︼紝瀵瑰簲鎴愯蛋鍚戝摢鏉¤矾
if (node.nexts[path] == null) {
node.nexts[path] = new Node1();
}
node = node.nexts[path];
node.pass++;
}
node.end++;
}
public void delete(String word) {
if (search(word) != 0) {
char[] chs = word.toCharArray();
Node1 node = root;
node.pass--;
int path = 0;
for (int i = 0; i < chs.length; i++) {
path = chs[i] - 'a';
if (--node.nexts[path].pass == 0) {
node.nexts[path] = null;
return;
}
node = node.nexts[path];
}
node.end--;
}
}
// word杩欎釜鍗曡瘝涔嬪墠鍔犲叆杩囧嚑娆�
public int search(String word) {
if (word == null) {
return 0;
}
char[] chs = word.toCharArray();
Node1 node = root;
int index = 0;
for (int i = 0; i < chs.length; i++) {
index = chs[i] - 'a';
if (node.nexts[index] == null) {
return 0;
}
node = node.nexts[index];
}
return node.end;
}
// 鎵�鏈夊姞鍏ョ殑瀛楃涓蹭腑锛屾湁鍑犱釜鏄互pre杩欎釜瀛楃涓蹭綔涓哄墠缂�鐨�
public int prefixNumber(String pre) {
if (pre == null) {
return 0;
}
char[] chs = pre.toCharArray();
Node1 node = root;
int index = 0;
for (int i = 0; i < chs.length; i++) {
index = chs[i] - 'a';
if (node.nexts[index] == null) {
return 0;
}
node = node.nexts[index];
}
return node.pass;
}
}
实现,方法二:当题目中字符串出现的字符种类很多时,Node内部使用哈希表存储字符。
public static class Node2 {
public int pass;
public int end;
public HashMap<Integer, Node2> nexts;
public Node2() {
pass = 0;
end = 0;
nexts = new HashMap<>();
}
}
public static class Trie2 {
private Node2 root;
public Trie2() {
root = new Node2();
}
public void insert(String word) {
if (word == null) {
return;
}
char[] chs = word.toCharArray();
Node2 node = root;
node.pass++;
int index = 0;
for (int i = 0; i < chs.length; i++) {
index = (int) chs[i];
if (!node.nexts.containsKey(index)) {
node.nexts.put(index, new Node2());
}
node = node.nexts.get(index);
node.pass++;
}
node.end++;
}
public void delete(String word) {
if (search(word) != 0) {
char[] chs = word.toCharArray();
Node2 node = root;
node.pass--;
int index = 0;
for (int i = 0; i < chs.length; i++) {
index = (int) chs[i];
if (--node.nexts.get(index).pass == 0) {
node.nexts.remove(index);
return;
}
node = node.nexts.get(index);
}
node.end--;
}
}
public int search(String word) {
if (word == null) {
return 0;
}
char[] chs = word.toCharArray();
Node2 node = root;
int index = 0;
for (int i = 0; i < chs.length; i++) {
index = (int) chs[i];
if (!node.nexts.containsKey(index)) {
return 0;
}
node = node.nexts.get(index);
}
return node.end;
}
public int prefixNumber(String pre) {
if (pre == null) {
return 0;
}
char[] chs = pre.toCharArray();
Node2 node = root;
int index = 0;
for (int i = 0; i < chs.length; i++) {
index = (int) chs[i];
if (!node.nexts.containsKey(index)) {
return 0;
}
node = node.nexts.get(index);
}
return node.pass;
}
}
前缀树主要使用在:当题目中需要查询某个前缀出现的次数时,我们可以想方设法构造前缀树进行查询。
2. 不基于比较的排序——桶排序

-
桶排序是一种大思想(桶泛指容器),计数排序就是桶排序的一种。桶可以是队列、栈、链表等。
-
基数排序的实现:
使用了前缀和数组
// only for no-negative value public static void radixSort(int[] arr) { if (arr == null || arr.length < 2) { return; } radixSort(arr, 0, arr.length - 1, maxbits(arr)); } public static int maxbits(int[] arr) { int max = Integer.MIN_VALUE; for (int i = 0; i < arr.length; i++) { max = Math.max(max, arr[i]); } int res = 0; while (max != 0) { res++; max /= 10; } return res; } // arr[l..r]排序 , digit // l..r 3 56 17 100 3 public static void radixSort(int[] arr, int L, int R, int digit) { final int radix = 10; int i = 0, j = 0; // 有多少个数准备多少个辅助空间 int[] help = new int[R - L + 1]; for (int d = 1; d <= digit; d++) { // 有多少位就进出几次 // 10个空间 // count[0] 当前位(d位)是0的数字有多少个 // count[1] 当前位(d位)是(0和1)的数字有多少个 // count[2] 当前位(d位)是(0、1和2)的数字有多少个 // count[i] 当前位(d位)是(0~i)的数字有多少个 int[] count = new int[radix]; // count[0..9] for (i = L; i <= R; i++) { // 103 1 3 // 209 1 9 j = getDigit(arr[i], d); count[j]++; } for (i = 1; i < radix; i++) { count[i] = count[i] + count[i - 1]; } for (i = R; i >= L; i--) { j = getDigit(arr[i], d); help[count[j] - 1] = arr[i]; count[j]--; } for (i = L, j = 0; i <= R; i++, j++) { arr[i] = help[j]; } } } public static int getDigit(int x, int d) { return ((x / ((int) Math.pow(10, d - 1))) % 10); }使用前缀和数组来优化桶排序的队列空间,模拟队列最后出队的顺序。
思路:使用一个count数组,保存当前位(d位)数字小于等于i的数有多少个count[i]。然后出队列时,将原数组从后往前遍历,取出当前位的数为多少,然后放在辅助控件的count[i]-1位置上。因为后加入队列的最后出队列,根据桶排序的思路,它将被放在当前位小于等于i的数字中的最后一个位置上。然后将计数减1,此后循环。

第六节 链表相关面试题

1. 链表快慢指针的使用

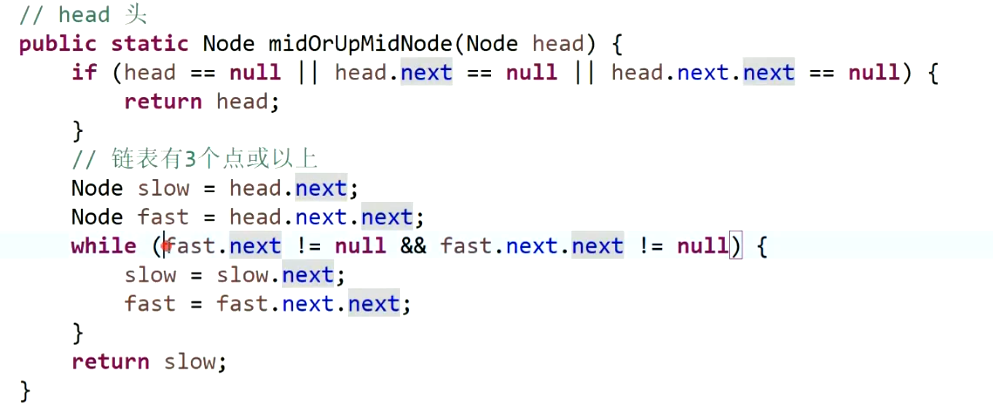
需要注意的是四种情况的边界条件。快慢指针实现的复杂度为O(N)
情况1:奇数返回中点,偶数返回上中点
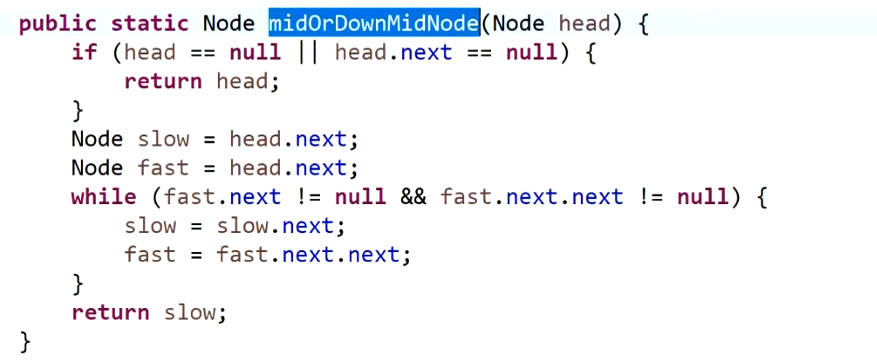
情况2:奇数返回中点,偶数返回下中点
情况3:奇数返回中点前一个,偶数返回上中点前一个
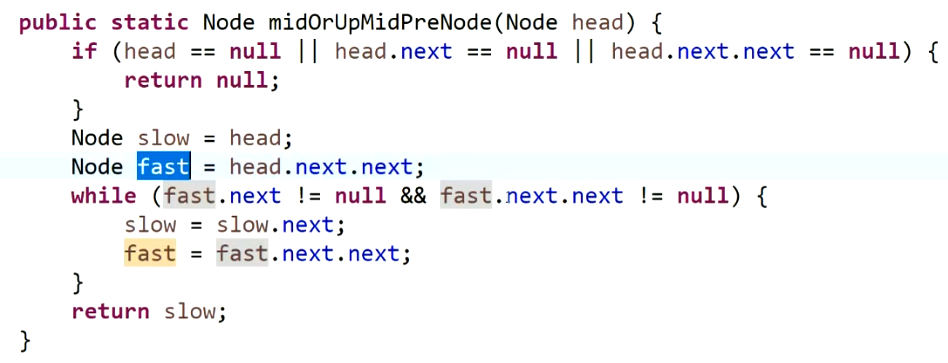
情况4:奇数返回中点前一个,偶数返回下中点前一个

2. 链表常见面试题
-
检测给定链表是否为回文链表:
- 使用一个栈
- 使用快慢指针拆成两个链表进行比较
-
将单向链表按照荷兰国旗问题划分:

思路,使用6个指针进行存储每个区的边界即可。
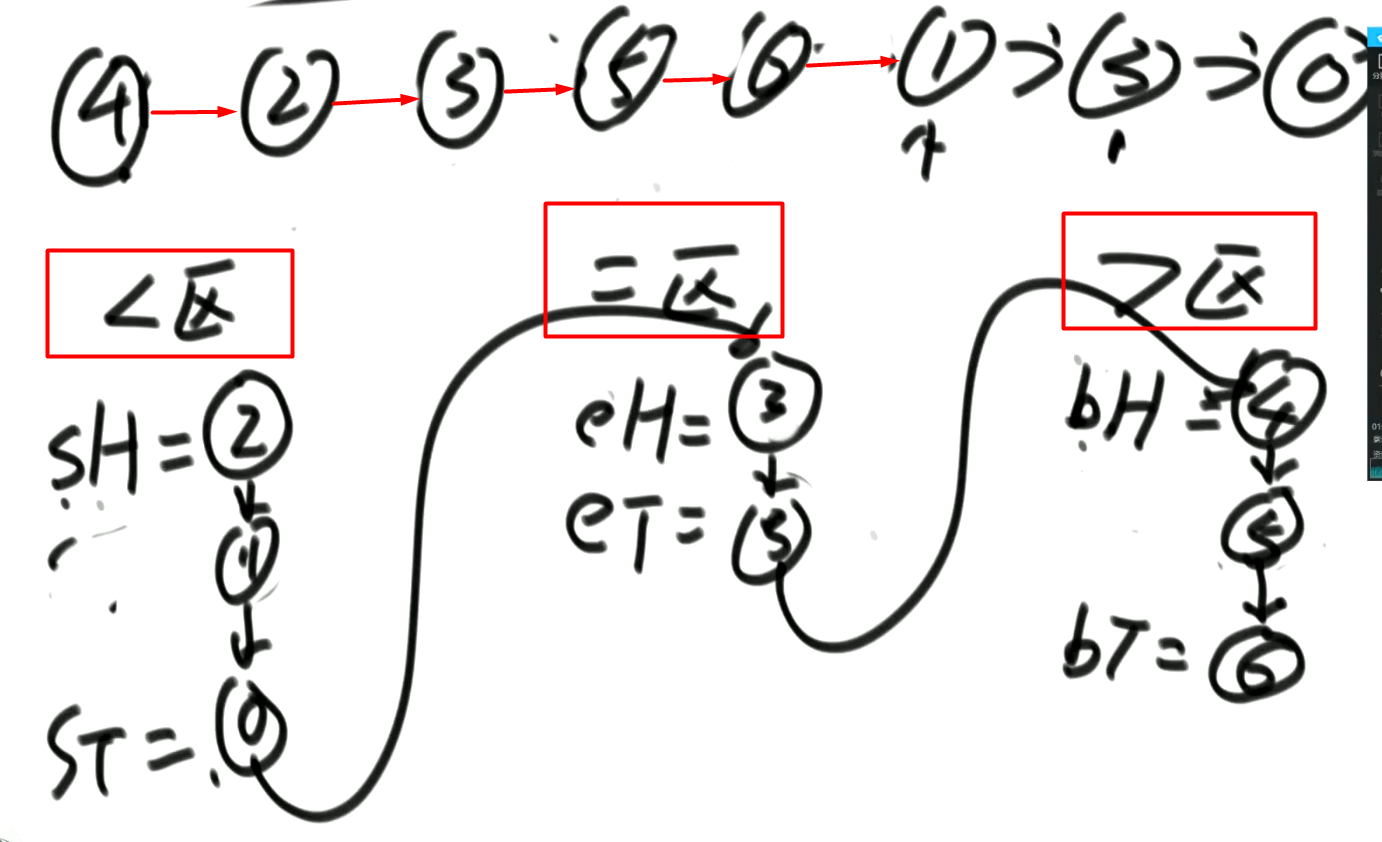
需要注意的是最后在串联链表的时候,需要判断小于区、等于区、大于区有没有结点:

-

思路1:使用一个
HashMap<Node,Node>,先通过next遍历一遍链表,将每个结点本身作为键,本身作为值放入Map中,然后进行克隆,每一个克隆操作都查表进行,结过再返回即可: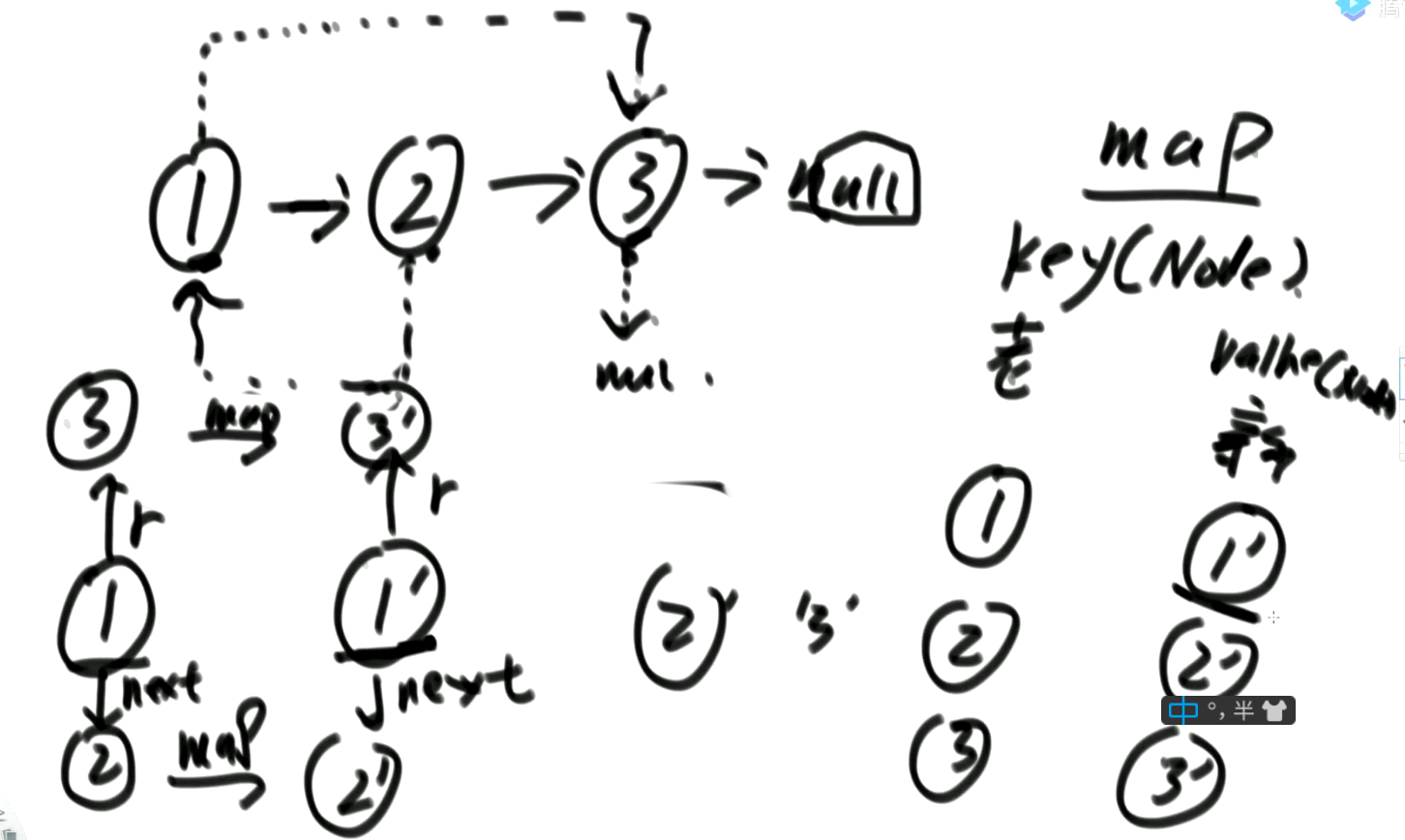
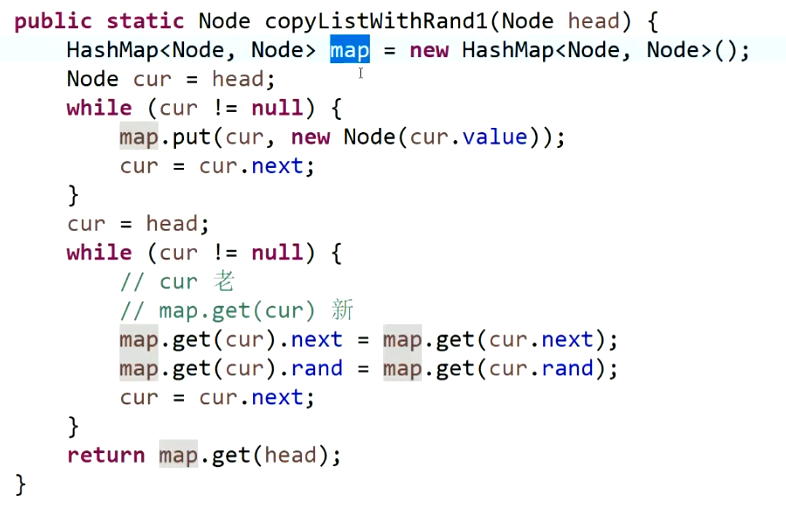
思路2:不使用哈希表
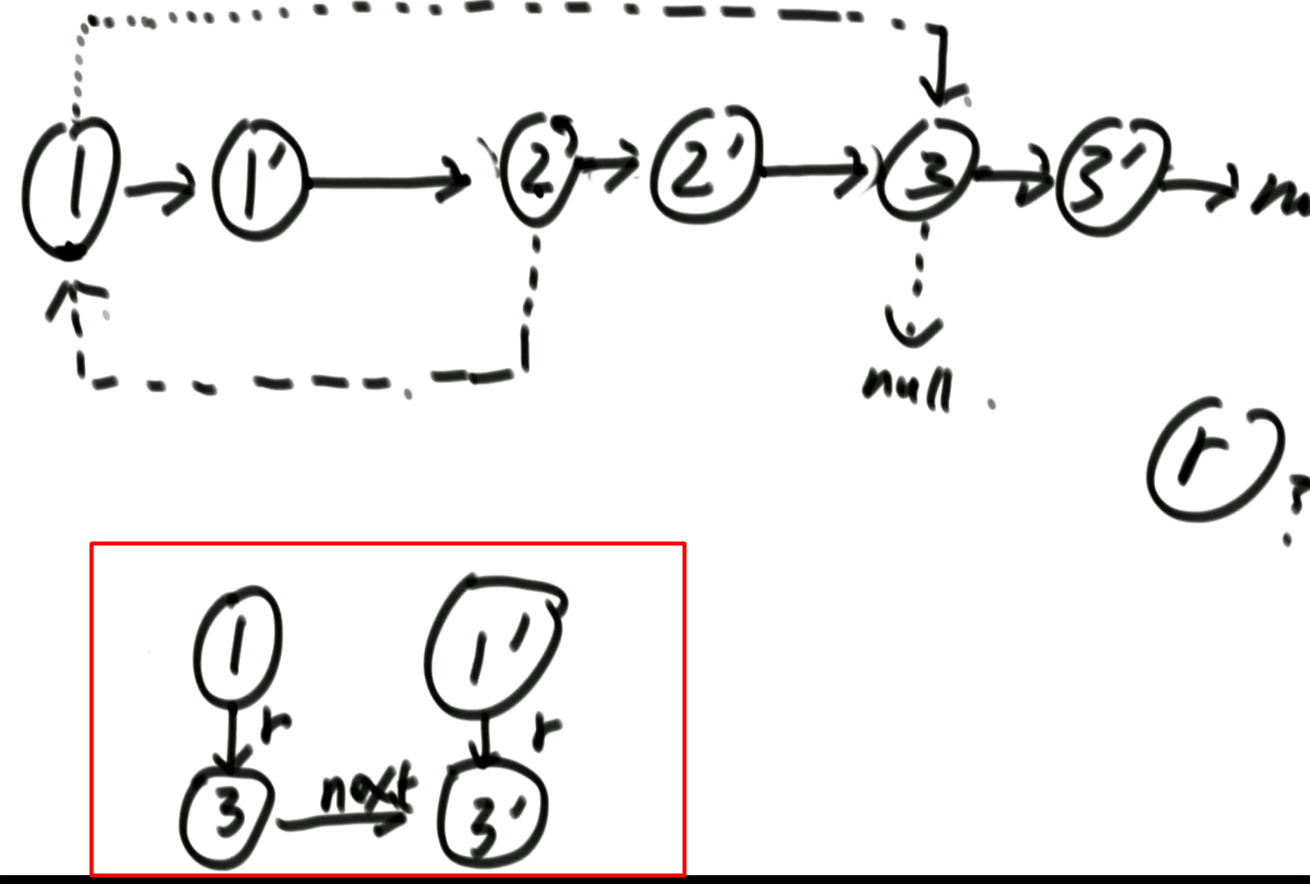
第一遍还是遍历每个结点,然后new一个新的结点放在当前结点之后,与原来的链表串联起来,将rand指针先悬空,这一步操作主要是人为的将复制出来的结点放在源节点之后。
第二步操作,从头遍历,每次取出一对结点,复制出来的结点的rand值就应该是其原本结点rand指向的next结点(因为有第一步的复制)
第三步,将整个链表进行分离,主要操作next指针,就不再关rand指针的事了。
-

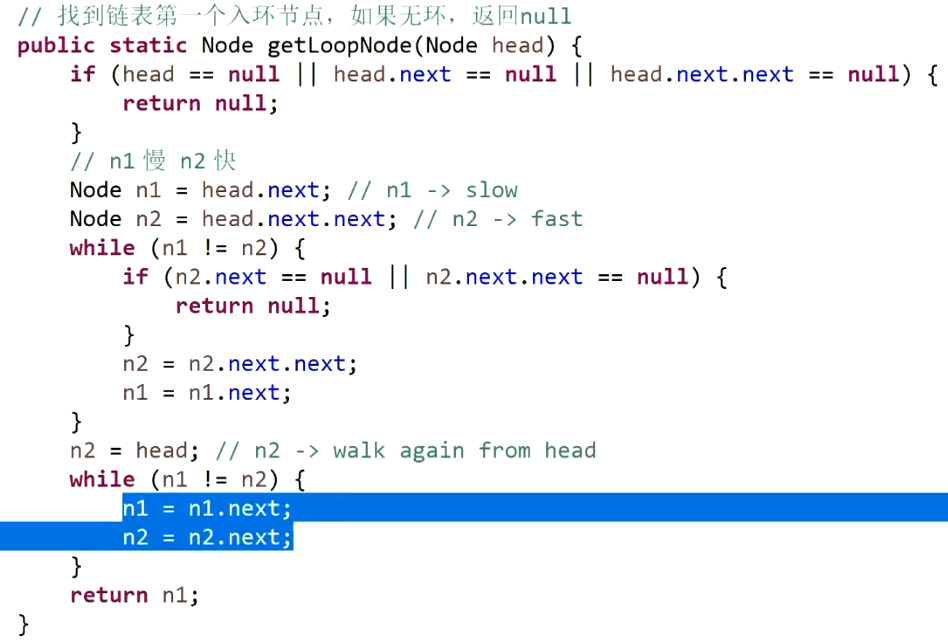
- 先设计一个方法,判断链表是否有环,并且返回链表形成环的第一个交点:
思路:
设计一个快慢指针,快指针一次两步,慢指针一次一步,有环时它们肯定会相遇;相遇后,快指针回到头部,变为一次一步,慢指针继续从相遇的地方一次一步走,下一次快慢指针相遇的地方就是链表环的第一个入口点。(数学定理)
-
接下来分情况讨论,情况1:如果是两个无环链表,判断是否相交
- 首选分别遍历两个链表,得到两个链表的长度已经最后一个结点的地址;
- 判断最后结点的地址是否相等,不相等肯定不相交;
- 相交的情况,较长的链表先走若干步,使得剩余的长度与较短的链表长度相等,此时就和较短的链表一同移动,它们就肯定会在第一个相交的结点相交。
-
情况2:一个链表有环、一个链表无环
这种情况两个链表不可能相交(链表的定义是最后一个结点指向null,每个结点只有一个next指针,只能指向一个结点)
-
情况3:两个链表都有环
注意:如果两个有环链表相交,他们一定是共用这个环的。有三种情况:
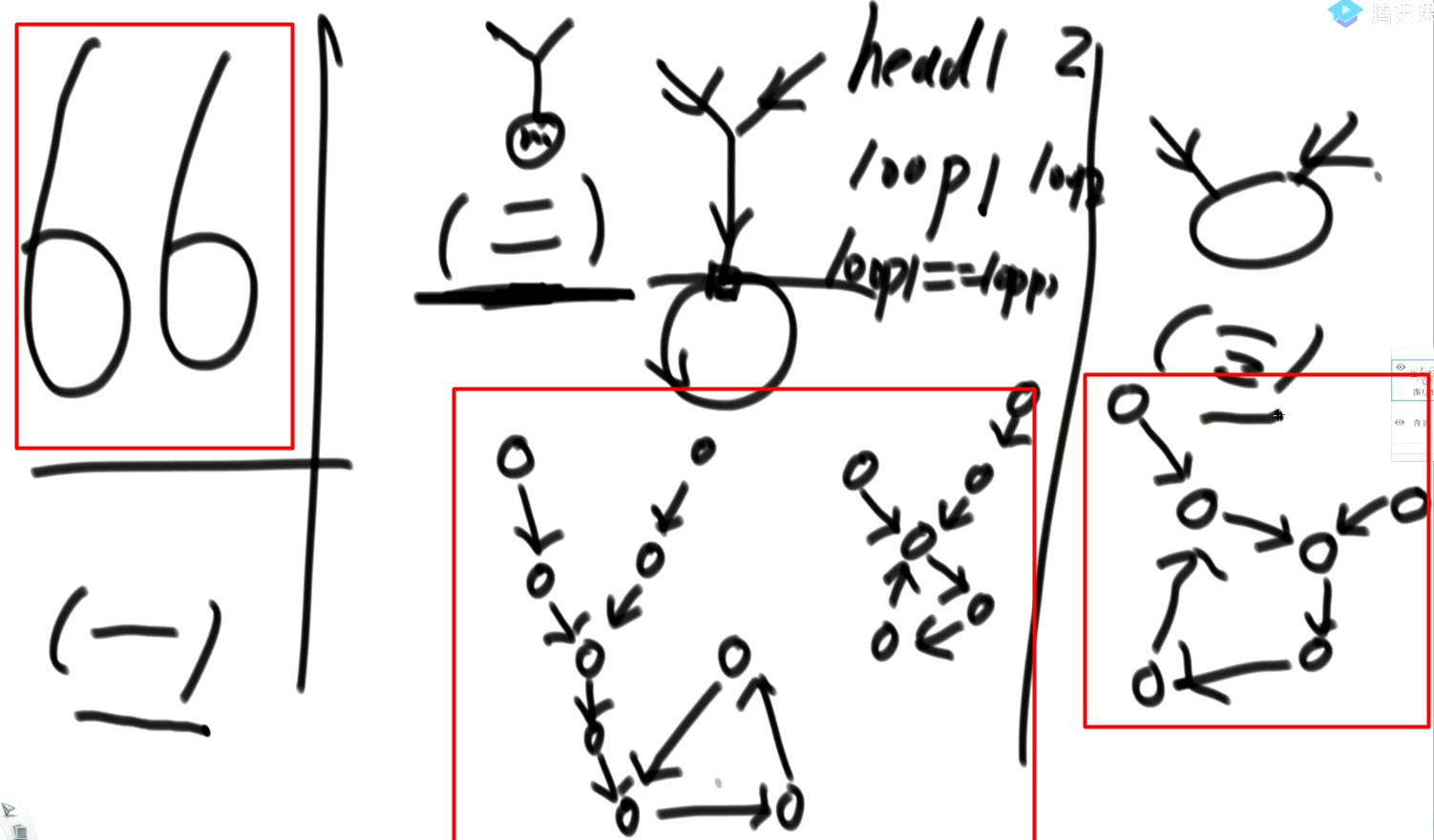
上图情况2:相交的第一个结点在入环的第一个结点或者环外。
此时只需要求出入环的第一个结点,以它作为终点,去求两个无环链表相交的第一个结点即可。退化为第一种大的情况。
区分上图情况1和情况3:
通过判断链表是否有环的方法,返回两个链表的第一个入环点,
loop1与loop2。然后从loop1结点继续向下走:- 如果能遇见loop2,则为情况三,这种情况返回值可以为loop1或loop3,因为这两个结点都算是两个链表相交的第一个结点;
- 如果不能遇见loop2,则为情况一,返回null,两个链表不相交。
-

思路1:(借尸还魂)
嘿嘿嘿,把要删除的结点的值,用其next结点的值覆盖掉,然后将要删除的结点next指向其next.next。也就是越过其后的结点。
思路2:
正常情况下,是不行的。给面试官解释Java内存引用的问题,还可以牵扯一些JVM的底层。
第七节 二叉树的基本算法
1. 二叉树的宽度搜索
二叉树的结点每一层都不一样,找到结点最多的那一层,返回结点数。
public static int maxWidthNoMap(Node head) {
if (head == null) {
return 0;
}
Queue<Node> queue = new LinkedList<>();
queue.add(head);
Node curEnd = head; // 当前层,最右节点是谁
Node nextEnd = null; // 下一层,最右节点是谁
int max = 0;
int curLevelNodes = 0; // 当前层的节点数
while (!queue.isEmpty()) {
Node cur = queue.poll();
if (cur.left != null) {
queue.add(cur.left);
nextEnd = cur.left;
}
if (cur.right != null) {
queue.add(cur.right);
nextEnd = cur.right;
}
curLevelNodes++;
if (cur == curEnd) {
max = Math.max(max, curLevelNodes);
curLevelNodes = 0;
curEnd = nextEnd;
}
}
return max;
}
2. 二叉树的序列化和反序列化
-
可以使用先序、后序或者按层遍历,来实现二叉树的序列化。不能使用中序遍历来序列化和反序列化二叉树:
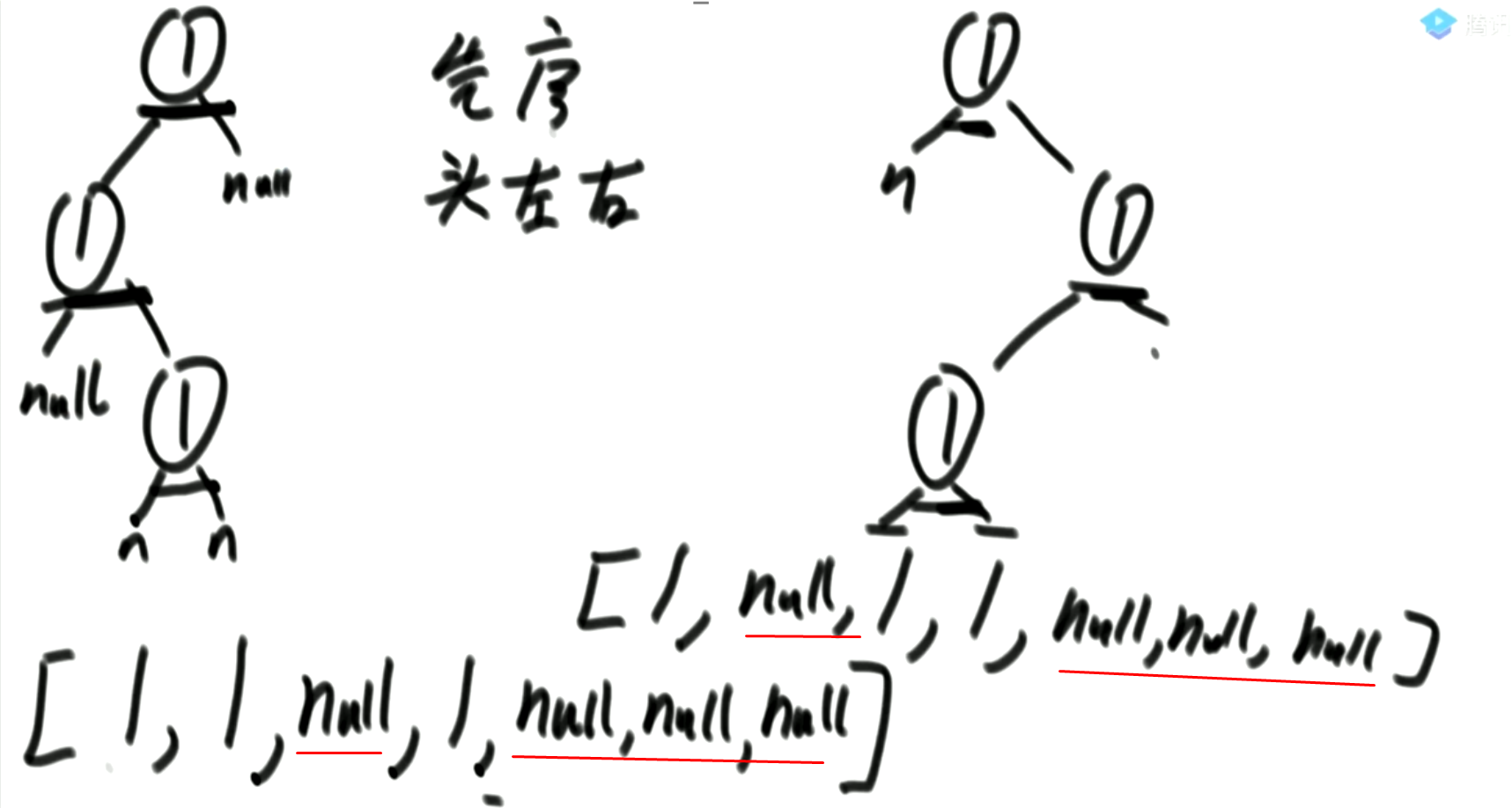
在先序或者中序后序遍历时,将不存在的结点用null补全,这样才可以完整存储二叉树的结构。
-
用了什么方式序列化,就用什么方式反序列化:
public static void pres(Node head, Queue<String> ans) { if (head == null) { ans.add(null); } else { ans.add(String.valueOf(head.value)); pres(head.left, ans); pres(head.right, ans); } } public static Node preb(Queue<String> prelist) { String value = prelist.poll(); if (value == null) { return null; } Node head = new Node(Integer.valueOf(value)); head.left = preb(prelist); head.right = preb(prelist); return head; } -
按层序列化二叉树:
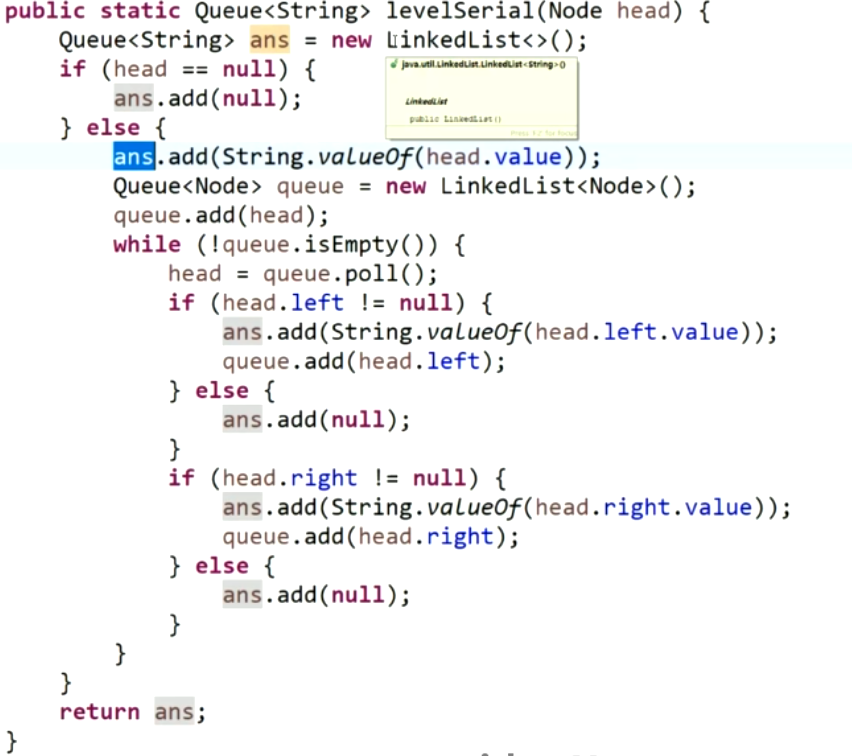
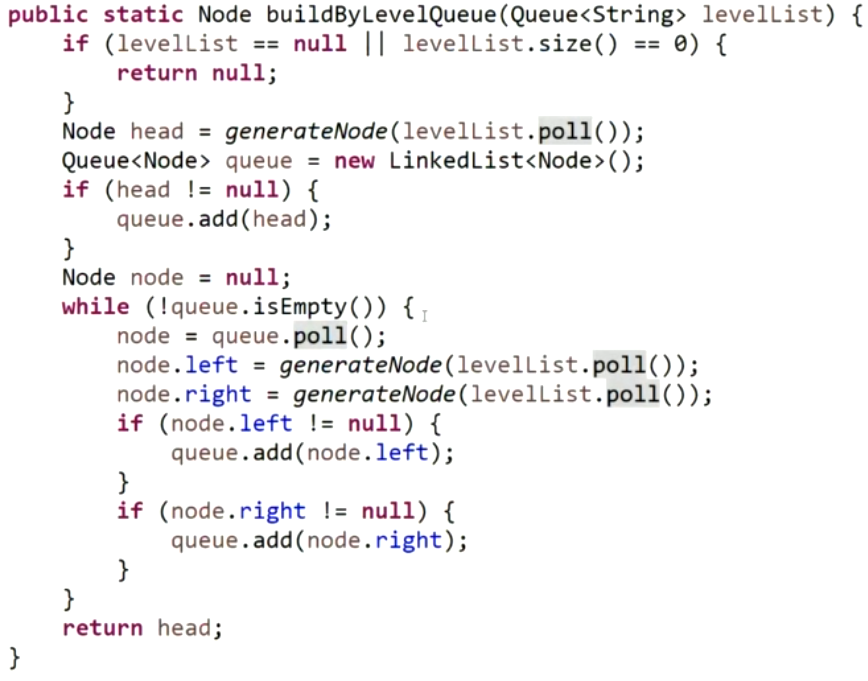
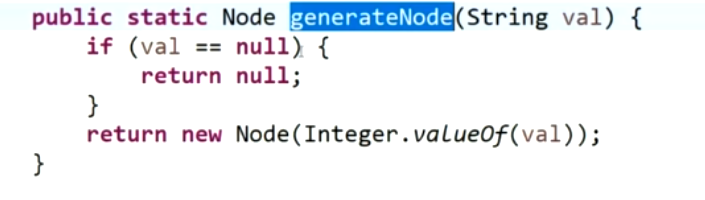
反序列化:
第八节 二叉树的递归套路
1. 二叉树相关面试笔试题
-
如何设计一个打印整棵树的打印函数(面试题)
-
给你一颗二叉树中的某一个结点,请你给出它的后继结点是谁,(后继结点指的是该结点在中序遍历过程中的后一个结点是什么)。
public static class Node { public int value; public Node left; public Node right; public Node parent; public Node(int data) { this.value = data; } } public static Node getSuccessorNode(Node node) { if (node == null) { return node; } if (node.right != null) { return getLeftMost(node.right); } else { // 无右子树 Node parent = node.parent; while (parent != null && parent.right == node) { // 当前节点是其父亲节点右孩子 node = parent; parent = node.parent; } return parent; } } public static Node getLeftMost(Node node) { if (node == null) { return node; } while (node.left != null) { node = node.left; } return node; }后继结点:中序遍历中一个结点的后一个结点;
前驱结点:中序遍历中一个结点的前一个结点。
思路:
当前结点的后继分两种情况。
一是当前结点有右子树时,那么他的后继就是右子树中最左的结点;
二是当前结点无右子树,那么他的后继就需要向上找,直到找到一个父节点的左子树为当前这一条分支的入口,那么该结点就是当前结点的后继。
-

分析:
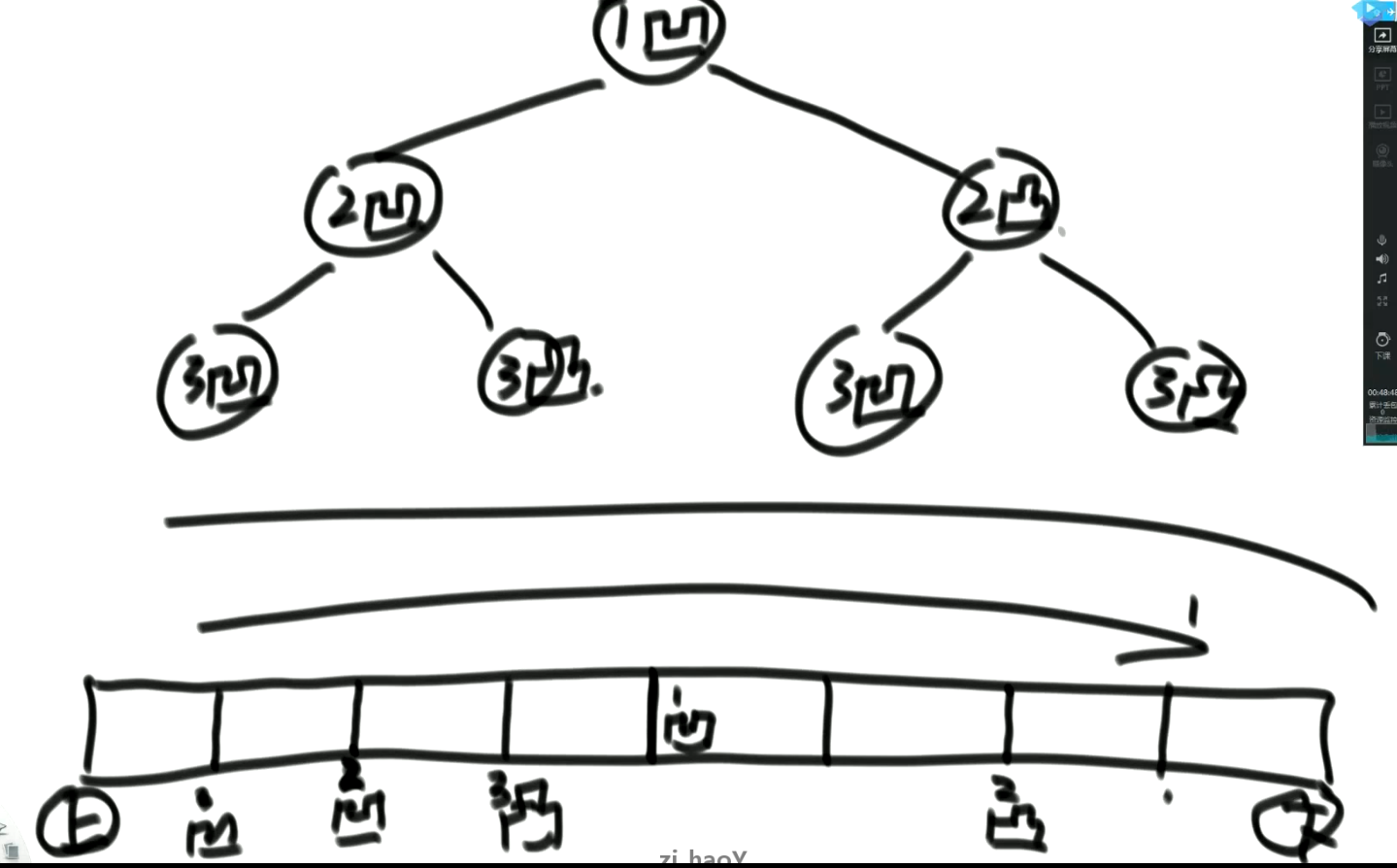
每一次都是在左子树产生凹折痕,右子树产生凸折痕。最后只需要模拟具有n层的这样的二叉树,对它进行中序遍历即可。
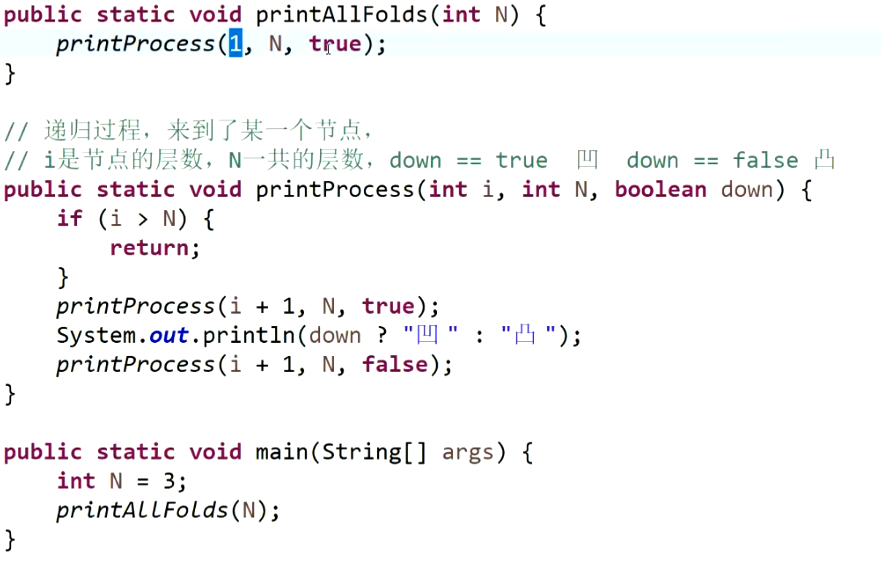
该方法,不需要建立出整个树,因为二叉树每个结点的规则已经确定了,所以不需要创建完整的一棵树。
2. 二叉树的递归套路
可以解决面试中绝大多数的二叉树问题尤其是树型dp问题,本质是利用递归遍历二叉树的便利性。
- 假设以X结点为头,假设可以向X左树和X右树要任何信息;
- 再上一步假设下,讨论以X为头结点的树,得到答案的可能性(最重要,就是分情况讨论);
- 列出所有可能性,确定到底需要向左树和右树要什么样的信息
- 把左树信息和右树信息求全集,就是任何一个子树都需要返回的信息S(这一步只是在左右子树要求的信息不一致时,才需要做)
- 递归函数都返回S,每一颗子树都这么要求
- 写代码,在代码中考虑如何把左树的信息和右树信息整合出整棵树的信息,要注意边界的判断。
-
给定一颗二叉树的头结点head,返回这颗二叉树是不是平衡二叉树:
平衡树:二叉树中每个结点的左子树高度与右子树高度差的绝对值不超过1:|左高 - 右高| <= 1
// 左、右要求一样,Info 信息返回的结构体 public static class Info { public boolean isBalaced; public int height; public Info(boolean b, int h) { isBalaced = b; height = h; } } public static Info process2(Node X) { if (X == null) { return new Info(true, 0); } Info leftInfo = process2(X.left); Info rightInfo = process2(X.right); int height = Math.max(leftInfo.height, rightInfo.height) + 1; boolean isBalanced = true; if (!leftInfo.isBalaced || !rightInfo.isBalaced || Math.abs(leftInfo.height - rightInfo.height) > 1) { isBalanced = false; } return new Info(isBalanced, height); }二叉树的递归套路也告诉我们如何去分析问题。
首先建立需要返回的信息,当前结点的二叉树是否为平衡二叉树,当前二叉树的高度;
然后递归的向左子树与右字数要信息,并且组合出当前结点的信息,返回给更上一层。
整合信息:当前层的高度为左右子树较大者+1;当前层是否为平衡二叉树,首先要看左右子树是否为平衡二叉树,并且当前层左右子树高度差不超过1.
-
给定一颗二叉树的头结点head,任何两个结点之间都存在距离,返回整棵二叉树的最大距离:
最大距离:二叉树中任意两个节点之间,从一个点到另一个点需要走多少步,使得整个距离最大。每个结点到本身的距离为1.
public static class Info { public int maxDistance; public int height; public Info(int dis, int h) { maxDistance = dis; height = h; } } public static Info process(Node X) { if (X == null) { return new Info(0, 0); } Info leftInfo = process(X.left); Info rightInfo = process(X.right); int height = Math.max(leftInfo.height, rightInfo.height) + 1; int maxDistance = Math.max( Math.max(leftInfo.maxDistance, rightInfo.maxDistance), leftInfo.height + rightInfo.height + 1); return new Info(maxDistance, height); }同样建立需要从左右子树需要返回的信息(每次建立信息的时候不要忘记,根节点也需要返回同样结构的数据)
询问左右子树,整合它们返回的信息给更高一层;
当前层子树的高度同上。
当前层子树的最大距离分两种情况:
一是不经过当前结点,只在其左或右子树中就已经形成了最大距离;另一种是需要经过当前结点,那么其最大距离就是左子树高度加右子树高度再加1;
整合信息后返回新的信息。
-
给定一颗二叉树的头结点head,返回这颗二叉树中最大的二叉搜索子树的结点数量:
二叉搜索树:整个树上没有重复的值,左子树都比根节点小,右子树都比根节点大。
建立信息,先分为两大类情况:
- 与当前结点X无关,那么最大的二叉搜索树肯定在左子树或者右子树当中;
- 与当前结点X有关,那么左子树必定是二叉搜索树,右子树也必定是二叉搜索树,且加上当前结点X,任然可以维持二叉搜索树的性质。即X结点的值大于左子树的最大值,小于右子树的最小值。
通过分析发现,我们对于左右子树要求的信息不同,
左子树要求的信息:最大搜索子树的Size、是否是最大搜索子树、左子树的最大值;
右子树要求的信息:最大搜索子树的Size、是否是最大搜索子树、右子树的最小值;
此时就需要对要求的信息求全集,因为是递归,所以返回信息要整体一致。
// 任何子树 public static class Info { public boolean isAllBST; public int maxSubBSTSize; public int min; public int max; public Info(boolean is, int size, int mi, int ma) { isAllBST = is; maxSubBSTSize = size; min = mi; max = ma; } } public static Info process(Node head) { if (head == null) { return null; } Info leftInfo = process(head.left); Info rightInfo = process(head.right); int min = head.value; int max = head.value; int maxSubBSTSize = 0; if (leftInfo != null) { min = Math.min(min, leftInfo.min); max = Math.max(max, leftInfo.max); maxSubBSTSize = Math.max(maxSubBSTSize, leftInfo.maxSubBSTSize); } if (rightInfo != null) { min = Math.min(min, rightInfo.min); max = Math.max(max, rightInfo.max); maxSubBSTSize = Math.max(maxSubBSTSize, rightInfo.maxSubBSTSize); } boolean isBST = false; if (//左树整体是搜索二叉树 (leftInfo == null ? true : (leftInfo.isAllBST && leftInfo.max < head.value)) && //右树整体是搜索二叉树 (rightInfo == null ? true : (rightInfo.isAllBST && rightInfo.min > head.value))) { isBST = true; maxSubBSTSize = (leftInfo == null ? 0 : leftInfo.maxSubBSTSize) + (rightInfo == null ? 0 : rightInfo.maxSubBSTSize) + 1; } return new Info(isBST, maxSubBSTSize, min, max); }然后,需要注意在数据使用之前需要判断是否为空,因为我们递归的时候返回了
null。情况1的话,就返回左右子树中最大的二叉搜索树的结点数量;如果是情况2的话,就需要返回左右子树加起来的节点数再加1的数量。 -
派对的最大快乐值问题:


分析:
对于每一个结点分为其来或者不来的快乐值(也就是与当前结点X相关和无关去讨论)。
如果和当前结点无关,那么需要整合的信息是:当前结点快乐值记为0,再加上它每个子树来或者不来的最大快乐值;
如果和当前结点有关,那么需要整合的信息是:当前结点快乐值加上,其所有子树不来的最大快乐值。
所以每个结点需要返回的信息结构是,当前结点要参加聚会时整棵树的最大快乐值,以及当前结点不参加聚会时的最大快乐值。
public static class Info { public int yes; public int no; public Info(int y, int n) { yes = y; no = n; } } public static Info process2(Employee x) { if (x.nexts.isEmpty()) { return new Info(x.happy, 0); } int yes = x.happy; int no = 0; for (Employee next : x.nexts) { Info nextInfo = process2(next); yes += nextInfo.no; no += Math.max(nextInfo.yes, nextInfo.no); } return new Info(yes, no); } -
判断一棵树是否为满二叉树
public static class Info { public int height; public int nodes; public Info(int h, int n) { height = h; nodes = n; } } public static Info process(Node head) { if (head == null) { return new Info(0, 0); } Info leftInfo = process(head.left); Info rightInfo = process(head.right); int height = Math.max(leftInfo.height, rightInfo.height) + 1; int nodes = leftInfo.nodes + rightInfo.nodes + 1; return new Info(height, nodes); }返回信息就是左右子树的节点数,然后满二叉树的判断条件是节点数 N = 2h - 1.
-
给定二叉树的头结点,返回二叉树中最大搜索子树的头结点
分析:与当前结点有关(当前结点形成了二叉搜索树)、与当前结点无关(当前结点与左右子树不能形成二叉搜索树)
返回信息:子树中最大搜索子树的头结点,子树中最大搜索子树的结点数,子树是否为二叉搜索树(可以省去这个信息,它可以由子树中最大搜索子树的头结点和自身的结点进行判断得到),子树的结点最大值,子树的结点最小值。
整合信息,注意边界
// 每一棵子树 public static class Info { public Node maxSubBSTHead; public int maxSubBSTSize; public int min; public int max; public Info(Node h, int size, int mi, int ma) { maxSubBSTHead = h; maxSubBSTSize = size; min = mi; max = ma; } } public static Info process(Node X) { if (X == null) { return null; } Info leftInfo = process(X.left); Info rightInfo = process(X.right); int min = X.value; int max = X.value; Node maxSubBSTHead = null; int maxSubBSTSize = 0; if (leftInfo != null) { min = Math.min(min, leftInfo.min); max = Math.max(max, leftInfo.max); maxSubBSTHead = leftInfo.maxSubBSTHead; maxSubBSTSize = leftInfo.maxSubBSTSize; } if (rightInfo != null) { min = Math.min(min, rightInfo.min); max = Math.max(max, rightInfo.max); if (rightInfo.maxSubBSTSize > maxSubBSTSize) { maxSubBSTHead = rightInfo.maxSubBSTHead; maxSubBSTSize = rightInfo.maxSubBSTSize; } } if ((leftInfo == null ? true : (leftInfo.maxSubBSTHead == X.left && leftInfo.max < X.value)) && (rightInfo == null ? true : (rightInfo.maxSubBSTHead == X.right && rightInfo.min > X.value))) { maxSubBSTHead = X; maxSubBSTSize = (leftInfo == null ? 0 : leftInfo.maxSubBSTSize) + (rightInfo == null ? 0 : rightInfo.maxSubBSTSize) + 1; } return new Info(maxSubBSTHead, maxSubBSTSize, min, max); } -
判断一棵树是否为完全二叉树
解法1:进行宽度优先遍历(凡是用到BFS,那么考虑使用队列结构),遍历过程中
- 任何结点,仅有右子树且无左子树,那么该树一定不是完全二叉树。
- 一旦遇到左右孩子不双全,后续遇到所有结点必须为叶子结点。
public static boolean isCBT1(Node head) { if (head == null) { return true; } LinkedList<Node> queue = new LinkedList<>(); // 是否遇到过左右两个孩子不双全的节点 boolean leaf = false; Node l = null; Node r = null; queue.add(head); while (!queue.isEmpty()) { head = queue.poll(); l = head.left; r = head.right; if ( // 如果遇到了不双全的节点之后,又发现当前节点不是叶节点 (leaf && (l != null || r != null)) || (l == null && r != null) ) { return false; } if (l != null) { queue.add(l); } if (r != null) { queue.add(r); } if (l == null || r == null) { leaf = true; } } return true; }解法2:
分析四种情况:
- 整棵树是满二叉树,那么一定是完全二叉树
- 左树是完全二叉树,右树是满二叉树,并且左树高度比右树高度大1,整棵树就是完全二叉树
- 左树是满二叉树,右树是满二叉树,左树比右树高度大1,整棵树就是完全二叉树
- 左树是满二叉树,右树是完全二叉树,左树与右树高度相等,整棵树就是完全二叉树
返回信息:子树是否为满二叉树、子树是否为完全二叉树、子树的高度
信息整合
// 对每一棵子树,是否是满二叉树、是否是完全二叉树、高度 public static class Info { public boolean isFull; public boolean isCBT; public int height; public Info(boolean full, boolean cbt, int h) { isFull = full; isCBT = cbt; height = h; } } public static Info process(Node X) { if (X == null) { return new Info(true, true, 0); } Info leftInfo = process(X.left); Info rightInfo = process(X.right); int height = Math.max(leftInfo.height, rightInfo.height) + 1; boolean isFull = leftInfo.isFull && rightInfo.isFull && leftInfo.height == rightInfo.height; boolean isCBT = false; if (isFull) { isCBT = true; } else { // 以x为头整棵树,不满 if (leftInfo.isCBT && rightInfo.isCBT) { if (leftInfo.isCBT && rightInfo.isFull && leftInfo.height == rightInfo.height + 1) { isCBT = true; } if (leftInfo.isFull && rightInfo.isFull && leftInfo.height == rightInfo.height + 1) { isCBT = true; } if (leftInfo.isFull && rightInfo.isCBT && leftInfo.height == rightInfo.height) { isCBT = true; } } } return new Info(isFull, isCBT, height); } -
给定一颗二叉树的头结点head,和另外两个结点a和b。返回a和b的最低公共祖先。
最低公共祖先:两个结点向上走时,最早遇到的共同父节点。
解法1:使用
HashSet。将整棵树遍历,用一张表保存每个结点的父节点。然后通过这张表,从a开始向上遍历,每过一个父节点,就加入HashSet中;最后再从b开始向上遍历,直到某个父节点已经出现在Set中的时候,就找出了最低公共祖先。解法2:
分情况讨论:假设判断当前结点是否为a和b的最低公共祖先,分为四种情况
- 当前结点不是a和b的最低公共祖先
- 当前结点的左子树上已经找到了a与b的最低公共祖先
- 当前结点的右子树上已经找到了a与b的最低公共祖先
- 当前结点已经确定发现了a和b结点,但是在左右子树上都没有答案,当前结点就是a和b的最低公共祖先
需要的信息:a与b分别是否已经发现、当前结点形成的数中a与b的最低公共祖先(也就是答案)。
信息整合:
// 任何子树, public static class Info { public Node ans; public boolean findO1; public boolean findO2; public Info(Node a, boolean f1, boolean f2) { ans = a; findO1 = f1; findO2 = f2; } } public static Info process(Node X, Node o1, Node o2) { if (X == null) { return new Info(null, false, false); } Info leftInfo = process(X.left, o1, o2); Info rightInfo = process(X.right, o1, o2); boolean findO1 = X == o1 || leftInfo.findO1 || rightInfo.findO1; boolean findO2 = X == o2 || leftInfo.findO2 || rightInfo.findO2; // O1和O2最初的交汇点在哪? // 1) 在左树上已经提前交汇了 // 2) 在右树上已经提前交汇了 // 3) 没有在左树或者右树上提前交汇,O1 O2 全了 // 4) 没有在当前结点X的整个树上找到o1与o2的交汇点 Node ans = null; if (leftInfo.ans != null) { ans = leftInfo.ans; } if (rightInfo.ans != null) { ans = rightInfo.ans; } if (ans == null) { if (findO1 && findO2) { ans = X; } } return new Info(ans, findO1, findO2); }
第九节 贪心算法

贪心算法的难点,在于证明局部最优解的过程可以得到全局最优解。
- 给定任意个字符串,将它们拼接在一起,返回拼接之后字典序最小的字符串。
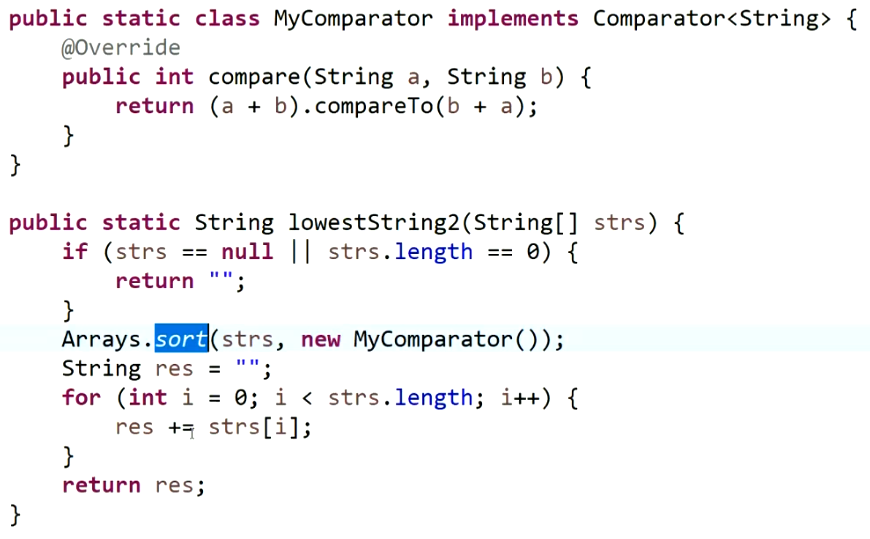
这里采取的贪心策略是: a + b <= b +a 且 b + c <= c + b 那么 a + c <= c + a。(这里的+代表字符串连接)
通过证明可以知道按照这个标准进行排序(两个字符串进行拼接,字典序小的排在前面),排序的结果是具有传递性的。(证明方法是将字符串作为一个26进制的数)
即: 如果只有两个字符串[a,b]按照上面的标准排好序之后,那么[b,a]的字典序一定大于前者。
同理,排好序的[a,b,c],那么[c,b,a]的字典序一定大于前者,[a,b,c,d] 一定小于[d,b,c,a]…
也就是将任意多个字符串按照两两拼接的字典序关系排好序之后,交换任意两个字符串,最后的结果都会使得字典序更大。
最后,根据数学归纳法,任意个字符串按照这个标准进行排序,最后从前到后拼接的结果就将是字典序最小的字符串。
贪心算法的结题套路

简单说就是用暴力算法来证明贪心策略是正确的。通过对数器进行验证。
在笔试中,贪心算法有60%左右的比重。
-
给定一个字符串为"XXXX…XXX…XX.X.XXX"的样式,其中X代表墙壁,"."代表一户人家,有人家的地方可以放一盏灯,一盏灯放的位置可以照亮左右各一户人家(共3户人家),求花最少的灯,将所有的人家照亮。
解法1:暴力解法
// str[index....]位置,自由选择放灯还是不放灯 // str[0..index-1]位置呢?已经做完决定了,那些放了灯的位置,存在lights里 // 要求选出能照亮所有.的方案,并且在这些有效的方案中,返回最少需要几个灯 public static int process(char[] str, int index, HashSet<Integer> lights) { if (index == str.length) { // 结束的时候 for (int i = 0; i < str.length; i++) { if (str[i] != 'X') { // 当前位置是点的话 if (!lights.contains(i - 1) && !lights.contains(i) && !lights.contains(i + 1)) { return Integer.MAX_VALUE; } } } return lights.size(); } else { // str还没结束 // i X . int no = process(str, index + 1, lights);//当前位置不放灯 int yes = Integer.MAX_VALUE; if (str[index] == '.') { lights.add(index); yes = process(str, index + 1, lights);//当前位置可以放灯,且放灯 lights.remove(index); } return Math.min(no, yes);//求二者的最小值返回 } }解法二:贪心
public static int minLight2(String road) { char[] str = road.toCharArray(); int index = 0; int light = 0; while (index < str.length) { if (str[index] == 'X') { index++; } else { // i -> . light++;//先放一盏灯,不用在意是在哪里放的,只需要在后面决定下一栈等放在哪里即可 if (index + 1 == str.length) { break; } else { if (str[index + 1] == 'X') { index = index + 2; } else { index = index + 3; } } } } return light; } -

贪心策略:反向合并,每次合并最小的两块,最后总的价格最低。哈夫曼树。
-
利润最大值。

贪心策略:
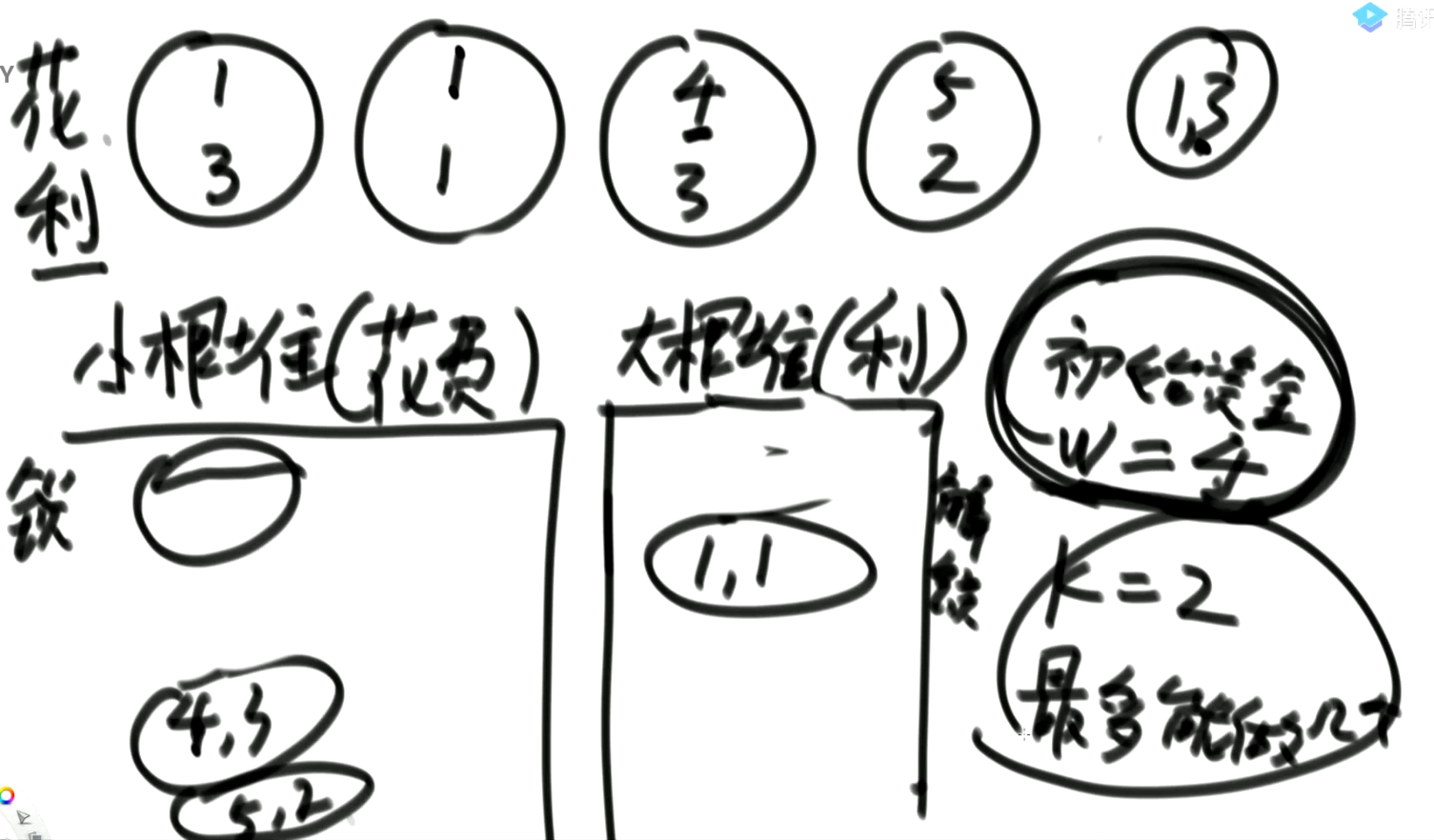
- 准备一个小顶堆(花费小的优先)、一个大顶堆(利润大的优先)
- 根据起始资金,去小根堆中找能够接的项目,将它们全部加入大根堆
- 从大根堆中选择一个利润最大项目做
- 然后获得新的资金后重复这个过程
public static int findMaximizedCapital(int K, int W, int[] Profits, int[] Capital) { PriorityQueue<Program> minCostQ = new PriorityQueue<>(new MinCostComparator()); PriorityQueue<Program> maxProfitQ = new PriorityQueue<>(new MaxProfitComparator()); for (int i = 0; i < Profits.length; i++) { minCostQ.add(new Program(Profits[i], Capital[i])); } for (int i = 0; i < K; i++) { while (!minCostQ.isEmpty() && minCostQ.peek().c <= W) { maxProfitQ.add(minCostQ.poll()); } if (maxProfitQ.isEmpty()) { return W; } W += maxProfitQ.poll().p; } return W; }
贪心的题基本上每一个题都不太一样,需要经验的累计,以及灵感爆发。
第十节 并查集结构和图的相关算法
1. 并查集

实现:
public class Code01_UnionFind {
public static class Node<V> {
V value;
public Node(V v) {
value = v;
}
}
public static class UnionSet<V> {
public HashMap<V, Node<V>> nodes;
public HashMap<Node<V>, Node<V>> parents;
public HashMap<Node<V>, Integer> sizeMap;
public UnionSet(List<V> values) {
for (V cur : values) {
Node<V> node = new Node<>(cur);
nodes.put(cur, node);
parents.put(node, node);
sizeMap.put(node, 1);
}
}
// 从点cur开始,一直往上找,找到不能再往上的代表点,返回
public Node<V> findFather(Node<V> cur) {
Stack<Node<V>> path = new Stack<>();//使用一个栈进行路径压缩
while (cur != parents.get(cur)) {
path.push(cur);
cur = parents.get(cur);
}
// cur头节点
while (!path.isEmpty()) {//调整路径
parents.put(path.pop(), cur);
}
return cur;
}
public boolean isSameSet(V a, V b) {
if (!nodes.containsKey(a) || !nodes.containsKey(b)) {
return false;
}
return findFather(nodes.get(a)) == findFather(nodes.get(b));
}
public void union(V a, V b) {
if (!nodes.containsKey(a) || !nodes.containsKey(b)) {
return;
}
Node<V> aHead = findFather(nodes.get(a));
Node<V> bHead = findFather(nodes.get(b));
if (aHead != bHead) {
int aSetSize = sizeMap.get(aHead);
int bSetSize = sizeMap.get(bHead);
Node<V> big = aSetSize >= bSetSize ? aHead : bHead;
Node<V> small = big == aHead ? bHead : aHead;
parents.put(small, big);
sizeMap.put(big, aSetSize + bSetSize);
sizeMap.remove(small);
}
}
}
}
常用的简化版并查集,仅使用数组实现
static final int MAX = 105;
static int[] parent = new int[105];
static int[] setsize = new int[105];
static int getParent(int x) {
if(x == parent[x])return x;
parent[x] = getParent(parent[x]);
return parent[x];
}
static boolean isSameSet(int x, int y) {
int px = getParent(x);
int py = getParent(y);
if(px == py) {
return true;
}
return false;
}
static void union(int x, int y) {
int px = getParent(x);
int py = getParent(y);
if(px != py) {
if(setsize[px] <= setsize[py]) {
parent[px] = py;
setsize[py] += setsize[px];
}else {
parent[py] = px;
setsize[px] += setsize[py];
}
}
}
static void init(int n) {
for(int i = 1;i <= n;i++) {
parent[i] = i;
setsize[i] = i;
}
}
2. 图论
-
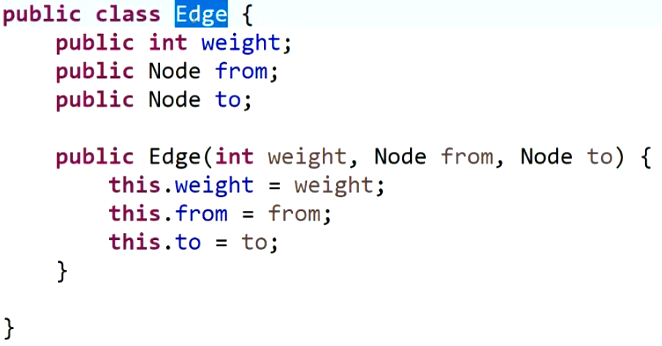
对于图的描述:
- 点结构的描述:

-
边的描述:
-
灵活的一种结构:
static class Edge{ public int to; public int w; public int next; { to = 0; w = 0; next = 0; } } private static int[] head = new int[MAXN];//每一个点起始的第一条边 private static Edge[] edge = new Edge[MAXN];//用于保存边 private static int cnt = 1;//1序 static void add(int from, int to, int w) { edge[cnt] = new Edge(); edge[cnt].to = to; edge[cnt].w = w; edge[cnt].next = head[from]; head[from] = cnt++; } //遍历方法 private static void solve() { cost[end] = 0; for(int i = end - 1;i >= 1;i--) { cost[i] = INF; } for(int j = end; j >= start;j--) { for(int i = head[j]; i != 0;i = edge[i].next) { if(edge[i].w + cost[j] < cost[edge[i].to]) { cost[edge[i].to] = edge[i].w + cost[j]; d[edge[i].to] = j; } } } } -
Dijkstra的实现,通过向前向量实现:
static void dijkstra(int n) { dist[1] = 0; for(int i = 1;i <= n;i++) { int ind = 0;//找一个点距离i最近的点,记录序号 for(int j = 1;j <= n;j++) { if(!vis[j] && (ind == 0 || dist[j] < dist[ind])) { ind = j; } } vis[ind] = true;//找到目前已知的能够到最短距离的点(且没有被调整过) for(int j = head[ind];j != 0;j = edge[j].next) {//通过目前知道距离最近的点,调整能够通过这个点到达的所有点,缩短距离。 if(dist[edge[j].to] > dist[ind] + edge[j].w) { dist[edge[j].to] = dist[ind] + edge[j].w; path[edge[j].to] = ind;//记录路径 } } } } -
Prim的实现,通过前向量实现:
static void prim(int start, int n) { for(int i = head[start];i != 0;i = edge[i].next) { dist[edge[i].next] = edge[i].w; } Arrays.fill(path, 1, n+1, start); dist[start] = 0; int ind, mind, sum = 0; //下面所说的集合内,表示已经生成好的最小生成树集合,最开始是一个点。 //集合外所代表的是,还没有加入最小生成树集合的点 for(int i = 1;i < n;i++) {//最小生成树只需要执行n-1步 ind = 0; mind = INF; for(int j = 1;j <= n;j++) {//找一个当前最小生成树集合(最开始是一个点)能够到达的最近的点 if(dist[j] != 0 && dist[j] < mind) { mind = dist[j]; ind = j; } } if(mind == INF) break;//没有找到 sum += mind;//计入最小生成树权值之和 dist[ind] = 0;//加入最小生成树集合,集合扩大,下次不再使用该点 for(int j = head[ind];j != 0;j = edge[j].next) { //通过找到的这个点,对其它在集合外的点进行松弛,看能不能通过找到的这个点缩短到集合外其它点的距离 if(dist[edge[j].to] != 0 && edge[j].w < dist[edge[j].to]) { dist[edge[j].to] = edge[j].w; path[edge[j].to] = ind; } } } System.out.println("最小生成树权值为:" + sum); } -
Kruskal的实现:
package com.yxs.graph1; import java.io.BufferedInputStream; import java.util.PriorityQueue; import java.util.Scanner; public class Kruskal { static class Edge{ int to, w, from; { to = w = from = 0; } } static final int MAXN = 105; static int[] head = new int[MAXN]; static Edge[] edge = new Edge[MAXN]; static int len = 1; static void add(int from, int to, int w) { edge[len] = new Edge(); edge[len].from = from; edge[len].to = to; edge[len++].w = w; } static int[] parent = new int[MAXN]; static int[] tnums = new int[MAXN]; static { for(int i = 0; i < parent.length;i++) { parent[i] = i; tnums[i] = 1; } } static int getParent(int x) { if(x == parent[x])return x; else return parent[x] = getParent(parent[x]); } static boolean isSameset(int x, int y) { int px = getParent(x); int py = getParent(y); if(px == py)return true; return false; } static void union(int x, int y) { int px = getParent(x); int py = getParent(y); if(px != py) { if(tnums[px] <= tnums[py]) { parent[px] = py; tnums[py] += tnums[px]; }else { parent[py] = px; tnums[px] += tnums[py]; } } } static void kruskal(int n) {//基于堆优化 PriorityQueue<Edge> queue = new PriorityQueue<>( (x, y)->{ return x.w - y.w; }); for(int i = 1;i < len;i++) { queue.add(edge[i]); } int ans = 0, cnt = 0; while(!queue.isEmpty() && cnt != n-1) { Edge e = queue.poll(); if(!isSameset(e.from,e.to)) { ans+=e.w; cnt++; union(e.from,e.to); } } System.out.println("最小生成树的权值为:" + ans); } public static void main(String[] args) { Scanner in = new Scanner(new BufferedInputStream(System.in)); int n = in.nextInt(); int e = in.nextInt(); for(int i = 1;i <= e;i++) { int from = in.nextInt(); int to = in.nextInt(); int w = in.nextInt(); add(from, to, w); } kruskal(n); } } /* 6 8 1 6 100 1 5 30 1 3 10 2 3 5 3 4 50 4 6 10 5 4 20 5 6 60 */
第十一节 暴力递归到动态规划

在这里之所以是暴力,是应为每一次不记录子问题的解,如果每一次记录子问题的解,那么就是动态规划。
-
给定一个栈,要求不使用额外的数据结构,使用递归函数,将整个栈逆翻转返回。
static void reverse(Stack stack) { if(stack.isEmpty()) { return; } Object obj = extract(stack); reverse(stack); stack.push(obj); } static Object extract(Stack stack) { Object obj = stack.pop(); if(stack.isEmpty()) { return obj; }else { Object last = extract(stack); stack.push(obj); return last; } }其中,reverse是用于翻转一个栈的递归方法,他有一个辅助方法extract。这个辅助方法每一次拿取栈底的元素,并且不破坏原来栈中的其它元素顺序。主方法就每次拿栈底元素直到栈为空的时候,在将拿到的元素通过递归栈一个个的放入栈中返回,就形成了逆序的栈。
重点是理解提取方法(extract),每次拿出当前栈顶元素,栈为空就直接返回,栈不为空,就继续递归的拿当前栈顶元素,拿空之后返回栈底元素,并将上一层元素放入栈中,最后返回栈底元素。
-
熟悉什么是尝试

-
动态规划都是某一类的暴力搜索的优化,会记录子集的解。
-
暴力搜索字符串的全部子序列:
public class T2 { static void dfs(char[] s, int pos, int start) { if(start == s.length)return; if(pos > s.length) { dfs(s, 0, start + 1); return; } for(int i = start;i < pos;i++) { System.out.print(s[i]); } if(pos > start)System.out.println(""); dfs(s, pos+1, start); } static void dfs2(char[] s, int pos, String t) { if(pos == s.length) { System.out.println(t); return; } dfs2(s, pos+1, t+s[pos]); dfs2(s, pos+1, t); } public static void main(String[] args) { String s = "abcd"; char[] ss = s.toCharArray(); dfs2(ss, 0, ""); System.out.println("================"); dfs(ss, 0, 0); } }其中,dfs函数搜索的是所有连续字符的子序列,dfs2搜索的是可以不连续字符的子序列,但是字符的相对位置于原字符串相等。
-
打印一个字符串的全部子序列,要求不出现重复字面值的子序列。做法,将答案保存在一个Set里面。
static void dfs3(char[] s, int pos, String path, HashSet<String> set) { if(pos == s.length) { if(!path.equals(""))set.add(path); return; } dfs3(s, pos+1, path+s[pos], set); dfs3(s, pos+1, path,set); } -
打印一个字符串的全部排列
static void dfs4(char[] s, int pos) { if(pos == s.length) { System.out.println(String.copyValueOf(s)); return; } for(int i = pos;i < s.length;i++) {//从当前位置开始,尝试将后面每个字符与当前位置交换 //代表pos位置后面的所有字符都可以与当前pos位置进行交换; swap(s, pos, i); dfs4(s, pos+1); swap(s, pos, i); //还原现场 } } -
打印一个字符串的全排列,去掉重复的字符串
static void dfs5(char[] s, int pos) { if(pos == s.length) { System.out.println(String.copyValueOf(s)); return; } boolean[] vis = new boolean[26];//用于保存当前位置用了哪些字符,用过的不能再使用了,这样就达到了分支定界的目的 for(int i = pos;i < s.length;i++) { if(!vis[s[i] - 'a']) {//判断当前位置是否使用过了第i个位置的字符 vis[s[i] - 'a'] = true; swap(s, pos, i); dfs5(s, pos+1); swap(s, pos, i); } //当前位置已经使用过i位置的字符的话,就不再递归这一条分支,直接减掉。 } }上面的vis数组只对每一个位置进行记录,记录这个位置已经使用过的字符,下一次再递归的时候,出现同样的字符时,该位置不再使用。这就是剪枝。
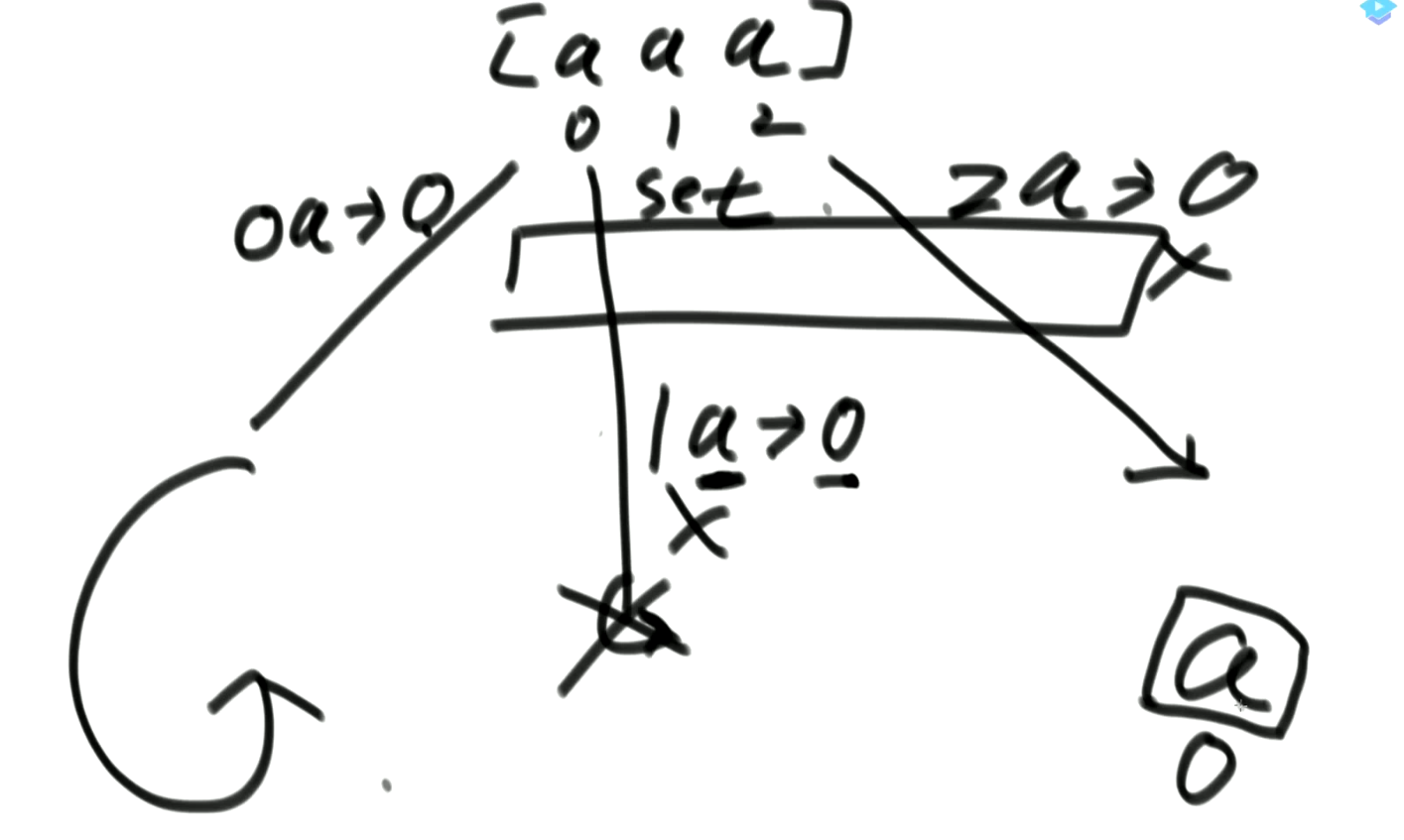
1. 搜索模型
常见的四种尝试模型:

1. 从左往右的尝试模型1:
//从左往右的尝试模型1
static int process(char[] str, int ind) {
if(ind == str.length) {
return 1;
}
if(str[ind] == '0') {
return 0;
}
if(str[ind] == '1') {
int ans = process(str, ind+1);
if(ind + 1 < str.length) {
ans += process(str, ind+2);
}
return ans;
}
if(str[ind] == '2') {
int ans = process(str,ind+1);
if(ind+1 < str.length && str[ind+1] >= '0' && str[ind+1] <= '6') {
ans += process(str, ind+2);
}
}
return process(str, ind+1);
}
分析:
题目只需要输出多少种抓换结果,所以就对转换结果进行搜索:
- 如果当前位置为0,则不能转换;
- 如果当前位置为1,则可以选择自己单独转换,或者与后面一个数结合一起转换;
- 如果当前位置为2,则可以选择自己单独转换,或者下一位不超过6的情况,可以一起结合转换;
- 如果当前位置大于等于3,只能单独转换。
- 如果当前位置已经到达字符串末尾,则已经形成一种转换结果。
2. 从左往右的尝试模型2:

01背包问题的搜索解决方案;
static int peocess(int[] w, int[] v, int ind, int W){//ind当前的物品,W当前背包剩余空间
if(W <= 0){
return 0;
}
if(ind == w.length){
return 0;
}
if(W < w[index]){
return process(w,v,ind+1,W);//剩余空间装不下,那么就不选当前物品
}else{
//能装下,则找一个较大者返回。
return Math.max(process(w,v,ind+1,W), v[ind] + process(w,v,ind+1,W-w[ind]));
}
}
3. 范围上尝试的模型

//先手函数
static int f(int[] arr, int L, int R){
if(L == R){
return arr[L];
}
return Math.max(
arr[L] + s(arr, L+1, R),
arr[R] + s(arr, L, R-1));
}
//后手函数
static int s(int[] arr, int L, int R){
if(L == R){
return 0;
}
return Math.min(
f(arr, L+1, R),
f(arr, L, R-1));
}
//返回先手与后手中获得的最大分数
static int win1(int[] arr){
if(arr == null || arr.length == 0){
return 0;
}
return Math.max(f(arr,0, arr.length-1), s(arr, 0, arr.length - 1));
}
例子分析:
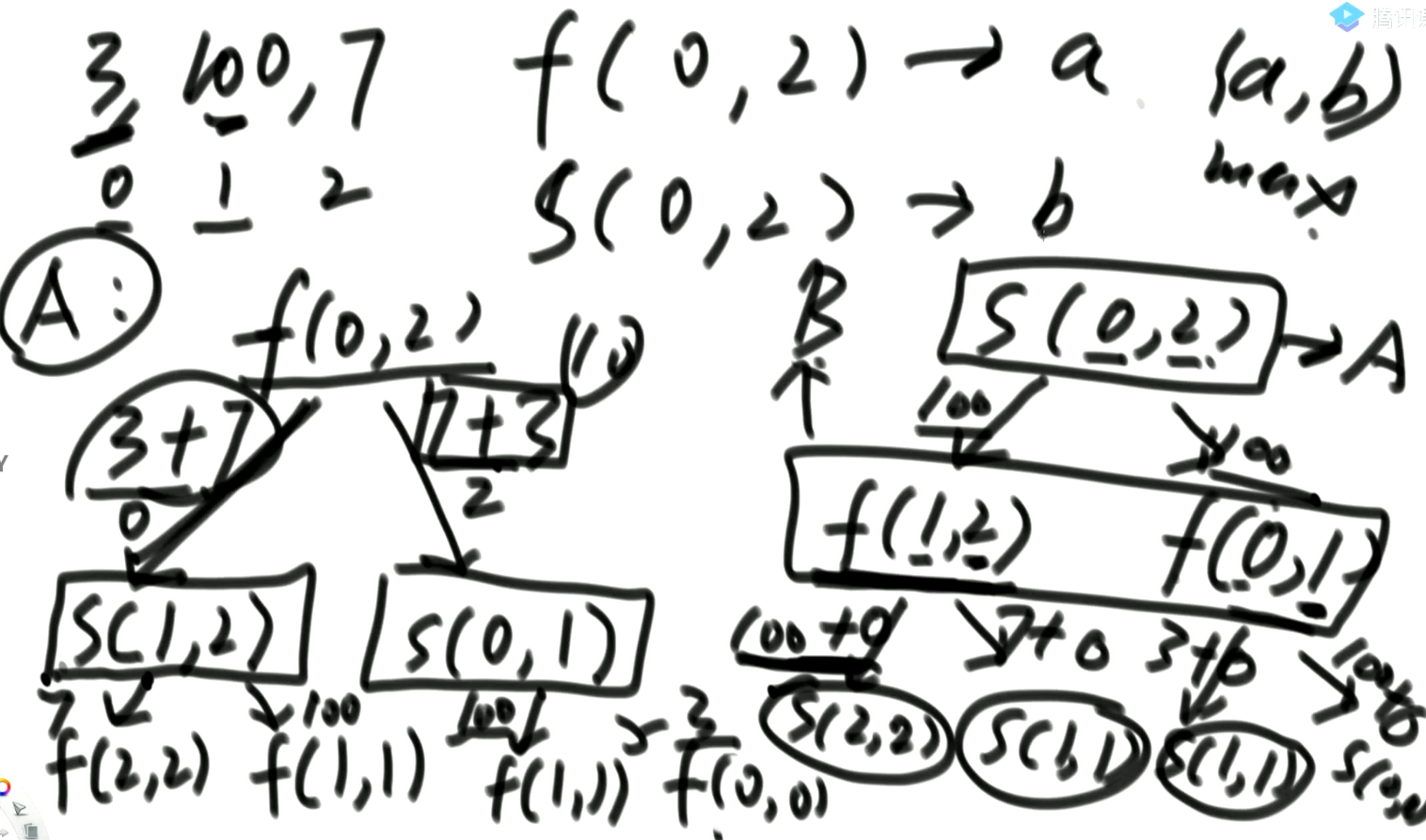
- f是先手函数,表示在L到R上先手的情况获得的分数。当在这个范围上先手拿牌时,只剩下一张牌的情况就直接返回这一张牌。
- s是后手函数,表示在L到R上后手的情况获得的分数。当在这个范围上后手拿牌时,因为只剩下一张牌,所以后手拿牌的得分是0。
- 先手函数会在arr左右选一张牌,最后结果是对自己最好的,并且下一次选牌将变为后手;
- 后手函数选牌时将变为先手,并且后手选牌一定会缩小1个范围,可能是左或右;由于先手足够聪明,所以后手函数只能获得缩小后的范围中【先手去拿的较小得分】(后手变先手),相当于一切在先手函数的计算当中。
4.其它的一些递归搜索
-
海盗分硬币问题,不同的前提,会得到不同的结果。100个硬币,分给5给海盗,每一个人提出分配方案,只有支持的数量大于一半的时候才会通过。
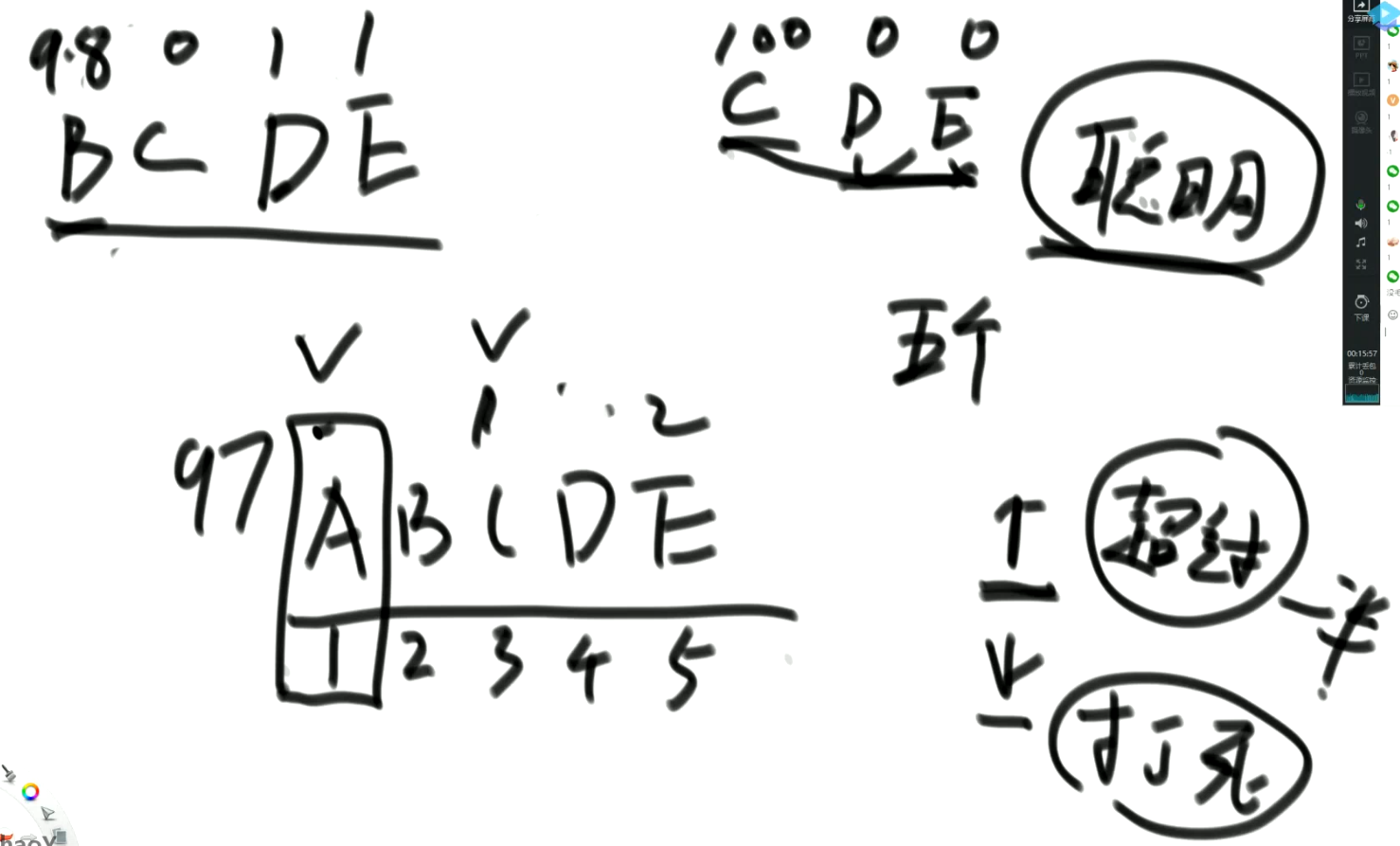
分析方法:
- 假设只有两个人DE,此时无论D提出什么方案,E都拒绝,那么E可以独自得到100金币;
- 假设有CDE三个人,此时C提出的最优方案为(100 0 0)。因为D此时的目的只是不想死,不论C会不会给自己分金币(两人情况下D必死),所以他会同意C。
- 假设有BCDE四个人,此时B提出的最优方案为(98 0 1 1)。B拉拢DE,因为只有三个人的时候,他们两个得不到金币,所以B给他们一人一个,那么DE相较与三个人的情况会选择支持B。
- 假设有ABCDE五个人,那么A最好拉拢的是C,因为只有四个人的时候,C一个金币也获得不了。所以给C一个,然后只需要再拉拢一个人,给D或者E两个金币,那么他们选择支持A,因为四个人的时候这个人只能拿到一个。(97 0 1 2 0)
-
一个村庄有n个人,规定每个人必须要寄出一封信,每个人必须收到一封信,自己不能寄给自己,求一共有多少种方案。
分析:
-
n==1的时候,方案数为0;
-
n==2的时候,方案数为1;(A->B,B->A)
-
n==3的时候,方案数为2;(A->B->C, A->C->B)
-
当n超过3时,假定一个函数f(n)返回n个人的方案数:
- 第n个人选择n-1个人中的任意一个,两个人相互寄出信件,然后只需要求剩下n-2个人的方案数。方案数:f(n) = (n-1)*f(n-2)
- 第n个人任选n-1个人寄出一封信,然后第n个人就可以与这个人在逻辑上称为一个人(这两个其中一个已经收到一封信,总共还需要寄出一封信收到一封信),所系方案数为:f(n)=(n-1)*f(n-1)
-
-
在坐标系,方格中验证两个点是否位于对角线的方法,实用。
令A(a, b) B(c,d)
假如|a-c| == |b-d|
那么就说A与B在网格的对角线中
常用于N皇后问题中两个皇后是否在同一斜线的判断。
-
N皇后问题,优化版。对于复杂度的优化,只是加速了常数时间,并不会影响最后的复杂度:
将皇后所放的列的限制改为实用整数位进行标志,左斜线限制与右斜线限制也使用整数位进行标志,准备一个
N个位的二进制数limit,用于确定位限制中的有效范围。- 当前在第0行,想要在某一列放皇后,放入皇后之后,对应列限制的位改为1,代表这里要放皇后;
- 那么对应就会生成下一行的左斜线与右斜线限制,将当前行放入皇后的列限制左移1位就是下一行的左斜线限制,同理右移1位就是下一行的右斜线限制。
- 进入第1行的时候,尝试在可以放皇后的列放皇后,先将列限制、左右斜线限制的位通过与运算并起来,成为总限制,将总线制再取反和
limit相与(忽略超过N的高位干扰),总线制为1的位在当前行才能放皇后,为0的位置则不能放皇后。 - 对处理过后的总线制,其每一个为1的位代表可以放皇后,依次取出每一位的1,进行遍历尝试。这里需要用到每次取出最右侧的1。
t = a & (~a + 1) - 当前行放皇后的位置确定之后,更新占用的列限制(或运算);对应的左右斜线限制,需要在上一行的左右斜线限制的当前列位置变为1(或运算),然后继续左移和右移,得到新的对于下一行的左右斜线限制。
- 右移时需要注意使用无符号右移,以免出现符号位被移入的情况。
public class N_Empless { //colbit位为1的代表对应列已经放了皇后 //leftbit位为1的代表对应位置在当前行不能放换后,有皇后的斜线经过 //rightbit同理 //limit代表N个1形成的数,用于规定进行位限制的这些数的有效范围 //index用于保存当前遍历的行数 //N代表N个皇后 static int dfs(int colbit, int leftbit, int rightbit, int limit, int index, int N) { if(index == N) { return 1; } int ans = 0; int sbit = colbit | leftbit | rightbit; sbit = ~sbit & limit; while(sbit != 0) { int col = sbit & (~sbit + 1);//当前可以放列所在的位 sbit -= col; ans += dfs(colbit | col, (leftbit | col) << 1, (rightbit | col) >>> 1, limit, index+1, N); } return ans; } public static void main(String[] args) { Scanner in = new Scanner(new BufferedInputStream(System.in)); int n = in.nextInt(); int limit = n == 32 ? -1 :(1 << n) - 1; int ans = dfs(0, 0, 0, limit, 0, n); System.out.println(ans); } }
2. 怎么尝试一件事——从暴力到动态规划

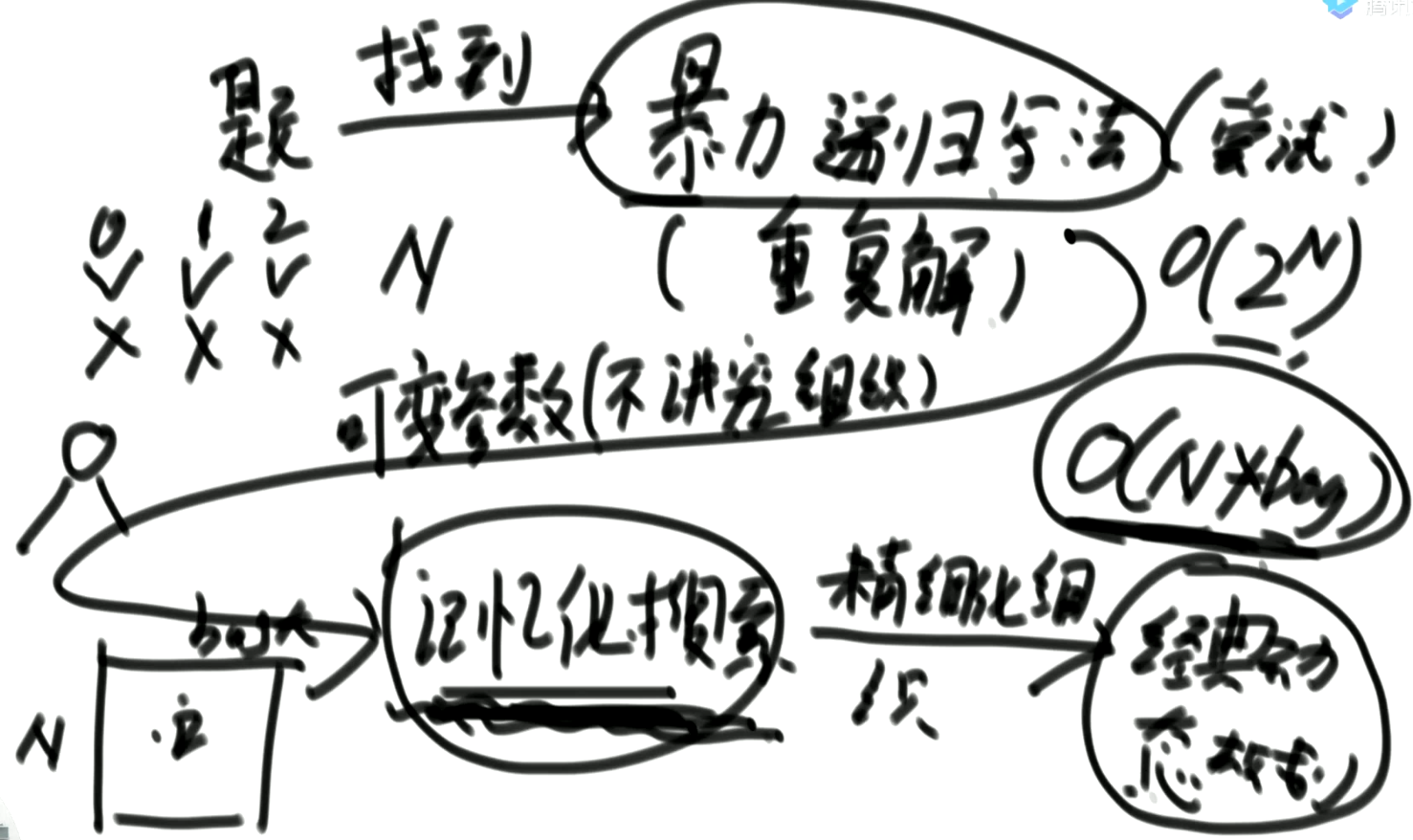
所有的暴力过程,都是因为有重复计算,所以才暴力。

1. 暴力搜索

注意:在尝试暴力解法的时候,最好把暴力解习惯性的写成有返回值的方法,这样有利于优化成动态规划;不要习惯了写没有返回值,利用全局遍历的暴力搜索过程。
2. 将暴力过程转换为没有状态依赖的动态规划(记忆化搜索)
因为我们在暴力搜索的时候,会有很多重复搜索的过程,所以我们将已经搜索的过程记录下来,然后下一次再搜索时直接返回。
那么保存已经搜索的各个状态,就需要一张表dp,这个dp表根据原来的搜索方法进行演变。
上面暴力搜索的方法中,N是不变的,P也是不变的,变化的只有cur、rest。所以保存状态的表就为dp[cur][rest],dp表的大小要能装下所有的情况。

可见,基于记忆化搜搜的动态规划,只是简单的记录每一次搜索状态的结果(将结果放入缓存),只是为了防止重复搜索。但是它还没有将动态规划中各个状态之间的依赖关系利用起来。
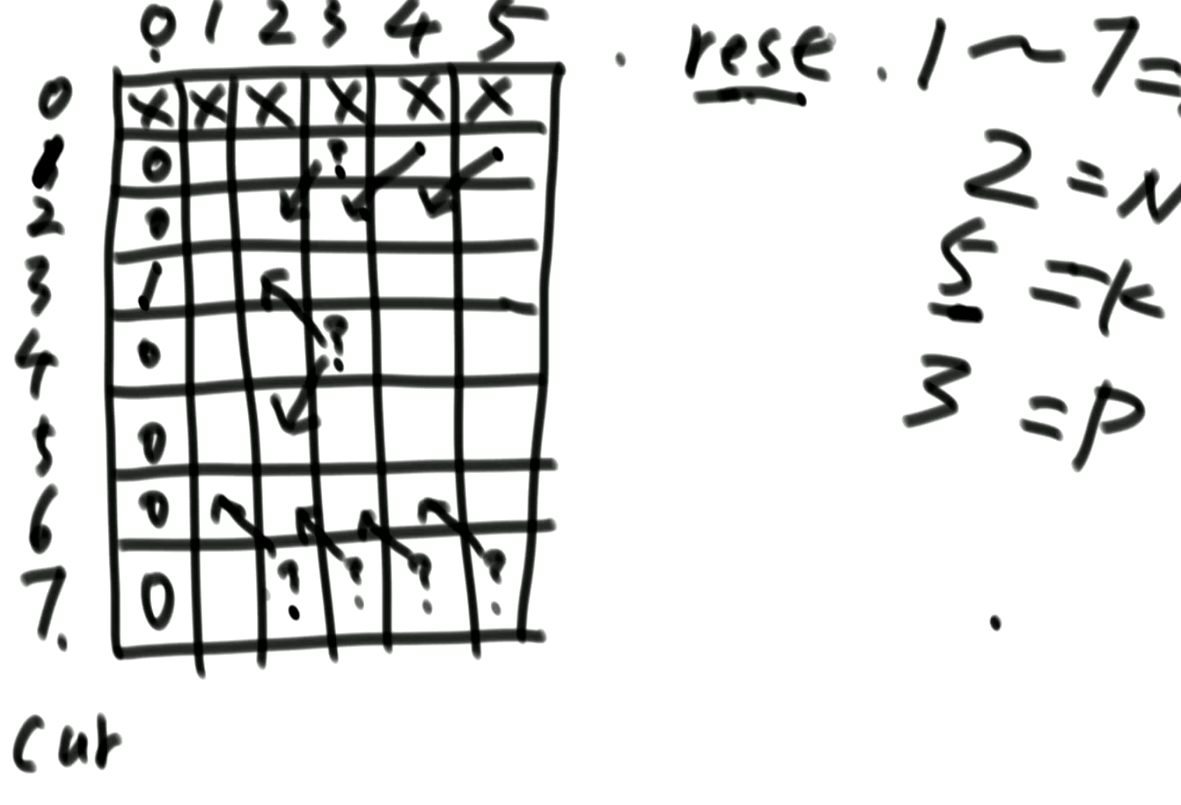
3. 依赖关系的确定
通过暴力记忆化搜索的过程,确定缓存表中各个位置的依赖情况。
- 当
cur == 1时,dp[cur][rest]依赖于dp[2][rest-1]; - 当
cur == N时,dp[cur][rest]依赖于dp[N-1][rest-1]; - 其它时候,
dp[cur][rest]依赖于dp[cur+1][rest-1]+dp[cur-1][rest-1];
通过暴力搜索过程,就可以直接得到动态规划中,各个状态之间的依赖关系。甚至在给出搜索代码的时候,我们就可以直接通过每一个搜索的状态转变,去确定缓存s表各个状态的关系,都不用在意原来的题意。
可见,动态规划的状态转移方程,就是由暴力搜索的各个决策抽象出来得到的,所以从最贴近自然的暴力搜索去尝试找动态规划的状态转移方程,是最容易的。
-
任何动态规划,都是由暴力搜索尝试的种子,改进过来的。
-
只要可变参数是有限的,并且可以通过暴力搜索去得到答案,那么我们就一定可以将它改进为动态规划!!!。
-
动态规划的过程,就是在将参数组合,变成缓存的过程。
-
需要注意的是,使用动态规划,需要看搜索过程是否有重复的状态,有重复的状态才有必要优化成动态规划,没有重复的状态时,就没必要用动态规划。
4. 将记忆搜索改为动态规划
public static int ways2(int N, int M, int K, int P) {
// 参数无效直接返回0
if (N < 2 || K < 1 || M < 1 || M > N || P < 1 || P > N) {
return 0;
}
int[][] dp = new int[K + 1][N + 1];
dp[0][P] = 1;
for (int i = 1; i <= K; i++) {
for (int j = 1; j <= N; j++) {
if (j == 1) {
dp[i][j] = dp[i - 1][2];
} else if (j == N) {
dp[i][j] = dp[i - 1][N - 1];
} else {
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j + 1];
}
}
}
return dp[K][M];
}
在实际根据搜索中决策改为状态转换方程的时候,需要注意填表的方向。
将dp表填满的具体方法:
-
根据搜索的决策,分析各个位置的依赖关系;
-
根据搜索的终止条件和边界条件,决定是从左往右填写还是从右往左填写。
-
最后需要的结果,要看调用搜索的调用状态。
-
在搜索的决策中,代码中所有递归调用函数的位置,都是需要改为
dp状态的位置。 -
dp就是用来保存暴力搜索中某一个状态的结果,所以说一个dp表就对应了一个搜索过程。
5. 转变为动态规划的例子
-
将背包问题的记忆化搜索改为动态规划
原来的暴力搜索:
static int peocess(int[] w, int[] v, int ind, int W){//ind当前的物品,W当前背包剩余空间 if(W <= 0){ return 0; } if(ind == w.length){ return 0; } if(W < w[index]){ return process(w,v,ind+1,W);//剩余空间装不下,那么就不选当前物品 }else{ //能装下,则找一个较大者返回。 return Math.max(process(w,v,ind+1,W), v[ind] + process(w,v,ind+1,W-w[ind])); } }转变成动态规划:
public static int dpWay(int[] w, int[] v, int bag) { int N = w.length; int[][] dp = new int[N + 1][bag + 1]; for (int index = N - 1; index >= 0; index--) { for (int rest = 1; rest <= bag; rest++) { dp[index][rest] = dp[index + 1][rest]; if (rest >= w[index]) { dp[index][rest] = Math.max(dp[index][rest], v[index] + dp[index + 1][rest - w[index]]); } } } return dp[0][bag]; } -
将数字转换为字符串,将其改为动态规划求解:
原来的暴力搜索
static int process(char[] str, int ind) {
if(ind == str.length) {
return 1;
}
if(str[ind] == '0') {
return 0;
}
if(str[ind] == '1') {
int ans = process(str, ind+1);
if(ind + 1 < str.length) {
ans += process(str, ind+2);
}
return ans;
}
if(str[ind] == '2') {
int ans = process(str,ind+1);
if(ind+1 < str.length && str[ind+1] >= '0' && str[ind+1] <= '6') {
ans += process(str, ind+2);
}
}
return process(str, ind+1);
}
改为动态规划
static int process(char[] s, int[] dp) {
if(s == null || s.length == 0 )return 0;
int N = s.length;
dp[N] = 1;
for(int i = N-1;i >= 0;i--) {
if(s[i] == '0') {
dp[i] = 0;
}
if(s[i] == '1') {
dp[i] = dp[i+1];
if(i+1 < N) {
dp[i] += dp[i+2];
}
}
if(s[i] == '2') {
dp[i] = dp[i+1];
if(i + 1 < N && s[i+1] >= '0' && s[i+1] <= '6') {
dp[i] += dp[i+2];
}
}
}
return dp[0];
}
-
动态规划的状态转移方程,就是对搜索决策的进一步抽象,实际上是同一个道理。所有的状态转移方程都来源于某一种搜索决策。
-
将A与B依次拿牌的问题,改为状态规划求解:
原暴力搜索:
//先手函数 static int f(int[] arr, int L, int R){ if(L == R){ return arr[L]; } return Math.max( arr[L] + s(arr, L+1, R), arr[R] + s(arr, L, R-1)); } //后手函数 static int s(int[] arr, int L, int R){ if(L == R){ return 0; } return Math.min( f(arr, L+1, R), f(arr, L, R-1)); } //返回先手与后手中获得的最大分数 static int win1(int[] arr){ if(arr == null || arr.length == 0){ return 0; } return Math.max(f(arr,0, arr.length-1), s(arr, 0, arr.length - 1)); }动态规划:
原来的暴力搜索中,具有两个搜索过程,所以我们需要两个缓存表,分别保存两个搜索的状态。
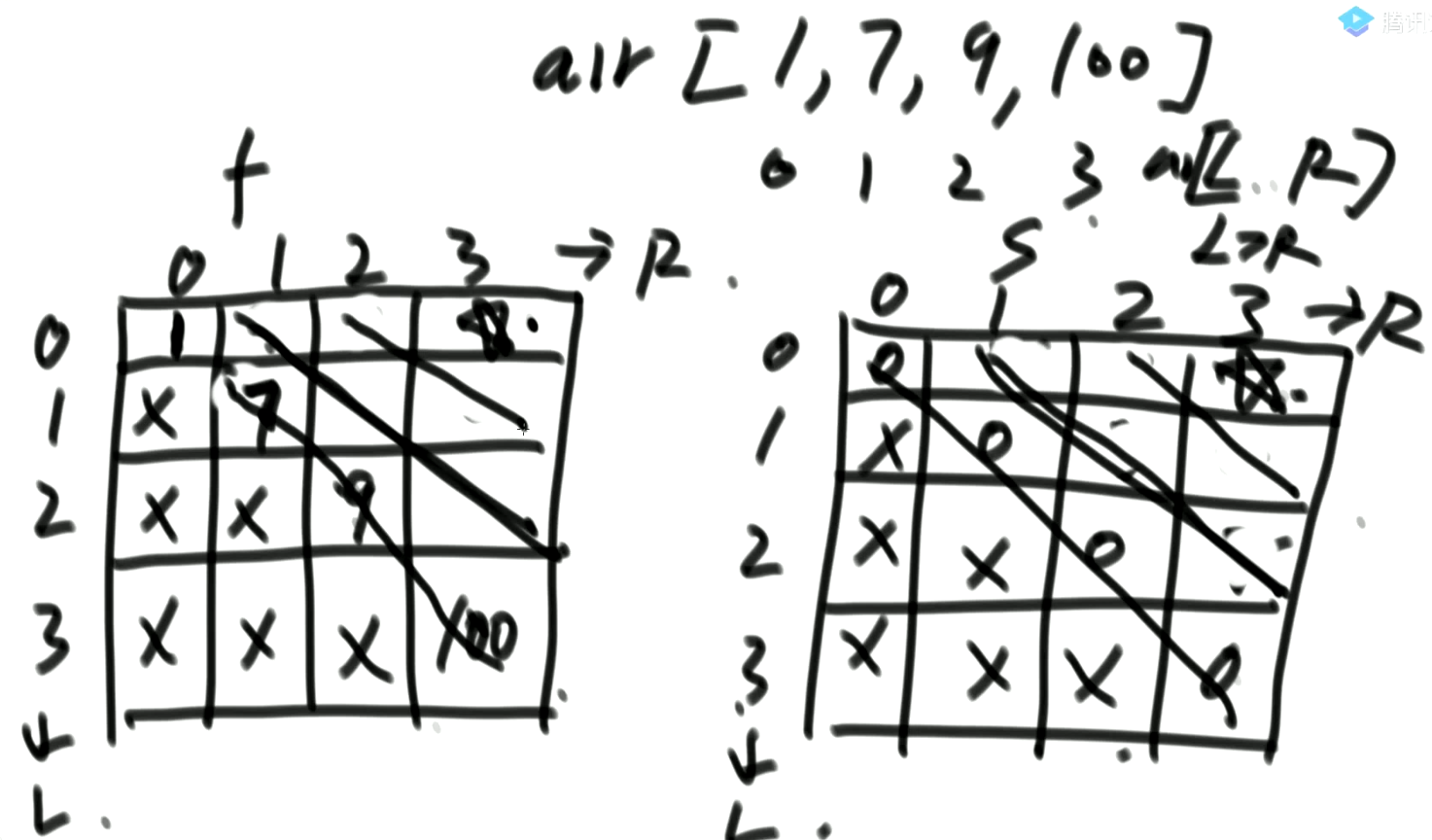
很多时候,可以根据搜索的决策,画出状态转移表,更方便我们转换为动态规划。
public static int win2(int[] arr) { if (arr == null || arr.length == 0) { return 0; } int N = arr.length; int[][] f = new int[N][N]; int[][] s = new int[N][N]; for(int i = 0; i < N;i++) {//根据f的终止状态得到 f[i][i] = arr[i]; } // s[i][i] = 0; 根据s的终止状态得到 for(int i = 1; i < N;i++) {//遍历状态表,进行状态转换 int L =0; int R =i; while(L < N && R < N) { f[L][R] = Math.max( arr[L] + s[L + 1][ R], arr[R] + s[L][R - 1] ); s[L][R] = Math.min( f[L + 1][R], // arr[i] f[L][R - 1] // arr[j] ); L++;//对状态表的对角线进行遍历。 R++; } } return Math.max(f[0][N-1], s[0][N-1]); }
3. 从暴力搜索到动态规划的一些例子
注意:当我们记忆化搜索中,每一次递归搜索只有有限个子状态时,那么就这一类的记忆化搜索问题转换为动态规划后,时间复杂度是一样的,也没有必要进行转换。
1. 多样本位置全对应的尝试模型
-
给定一个数组
arr[1...n],每一个数代表一种货币面值,现要求使用N种不同的货币面值,凑成1000的面值,问有多少种凑法,每种面值可以使用多次。- 暴力求解法:注意不同搜索思路存在一定的差异,需要看对结果的要求
static int dfs(int[] arr, int ins, int dest) { //这种搜索方式,将会导致最后搜索结果具有顺序性,即会把 5 5 10 10 和 5 10 5 10认为是两种情况。 //但是我们题目中只会把这种情况视为一种,所以说要加入其它的状态。 //这个搜索实际上只有一种状态,即现在搜索的货币凑了多少钱 if(ins > dest)return 0; if(ins == dest) { return 1; } int ans = 0; for(int i = 0;i < arr.length;i++) { ans += dfs(arr, ins+arr[i], dest); } return ans; } static int dfs2(int[] arr, int ind, int dest) { //使用这种搜索思路 //有两个转态,当前还需要凑多少钱,当前在尝试使用第几种货币 //将当前搜索的货币种类作为一个状态,那么就可以根据每一种货币使用的次数进行尝试,这样就不会得到上面那种重复的序列。 if(ind == arr.length) { return dest == 0 ? 1 : 0; } int ans = 0; for(int i = 0;i * arr[ind] <= dest;i++) { ans += dfs2(arr, ind + 1, dest - i *arr[ind]); } return ans; }- 将
dfs2改为动态规划(熟练之后可以直接由搜索改为动态规划),这是第一版,因为其中还含有枚举行为,不够简化。
static int process(int[] arr, int[][] dp, int dest) {//根据我们所找的搜索方法,缓存列表是一个二维的,因为有两个状态 dp[arr.length][0] = 1;//最初的状态,完全是根据暴力搜索抽象出来的缓存结构,就是暴力搜索中的一个状态,剩余钱为0,然后又尝试了每种货币,所以解就是1.不要尝试对这个数组有更复杂的理解,最终绕晕自己。理解搜索的过程。 for(int i = arr.length - 1;i >= 0;i--) {//根据终止状态,应该从后往前遍历。 //i遍历每一种货币,j遍历当前需要凑的钱数 for(int j = 0;j <= dest;j++) { //k遍历当前货币使用了多少张 for(int k = 0;k * arr[i] <= j;k++) { dp[i][j] += dp[i+1][j-k*arr[i]]; } } } return dp[0][dest]; } //完全由搜索过程抽象演变而来- 将枚举过程进行优化:
static int process(int[] arr, int[][] dp, int dest) {//根据我们所找的搜索方法,缓存列表是一个二维的,因为有两个状态 dp[arr.length][0] = 1;//最初的状态,完全是根据暴力搜索抽象出来的缓存结构,就是暴力搜索中的一个状态,剩余钱为0,然后又尝试了每种货币,所以解就是1.不要尝试对这个数组有更复杂的理解,最终绕晕自己。理解搜索的过程。 for(int i = arr.length - 1;i >= 0;i--) {//根据终止状态,应该从后往前遍历。 //i遍历每一种货币,j遍历当前需要凑的钱数 for(int j = 0;j <= dest;j++) { dp[i][j] = dp[i+1][j]; if(j - arr[i] >= 0){ dp[i][j] += dp[i][j-arr[i]]; } } } return dp[0][dest]; }优化枚举钱的张数分析:
对于
dp[i][j]的状态,通过搜索策略我们知道,这代表是要在从第i种货币开始,凑齐j金额的方案数。-
首先第
i种货币肯定可以选择0张,就会变成dp[i+1][j]从i+1种货币开始,凑齐j金额的方案数,先累加上。 -
第
i种货币选1张…k张的时候,就会由第i+1种货币去解决选j-k*arr[i]金额的方案数dp[i+1][j-k*arr[i]],加上当前第i种货币解决j金额的方案数,才是总的方案数。 -
而这些累加的和,已经在由第
i种货币解决j-k*arr[i]的时候计算过了,所以不需要再去枚举和,可以直接使用就是了。 -
举个栗子:
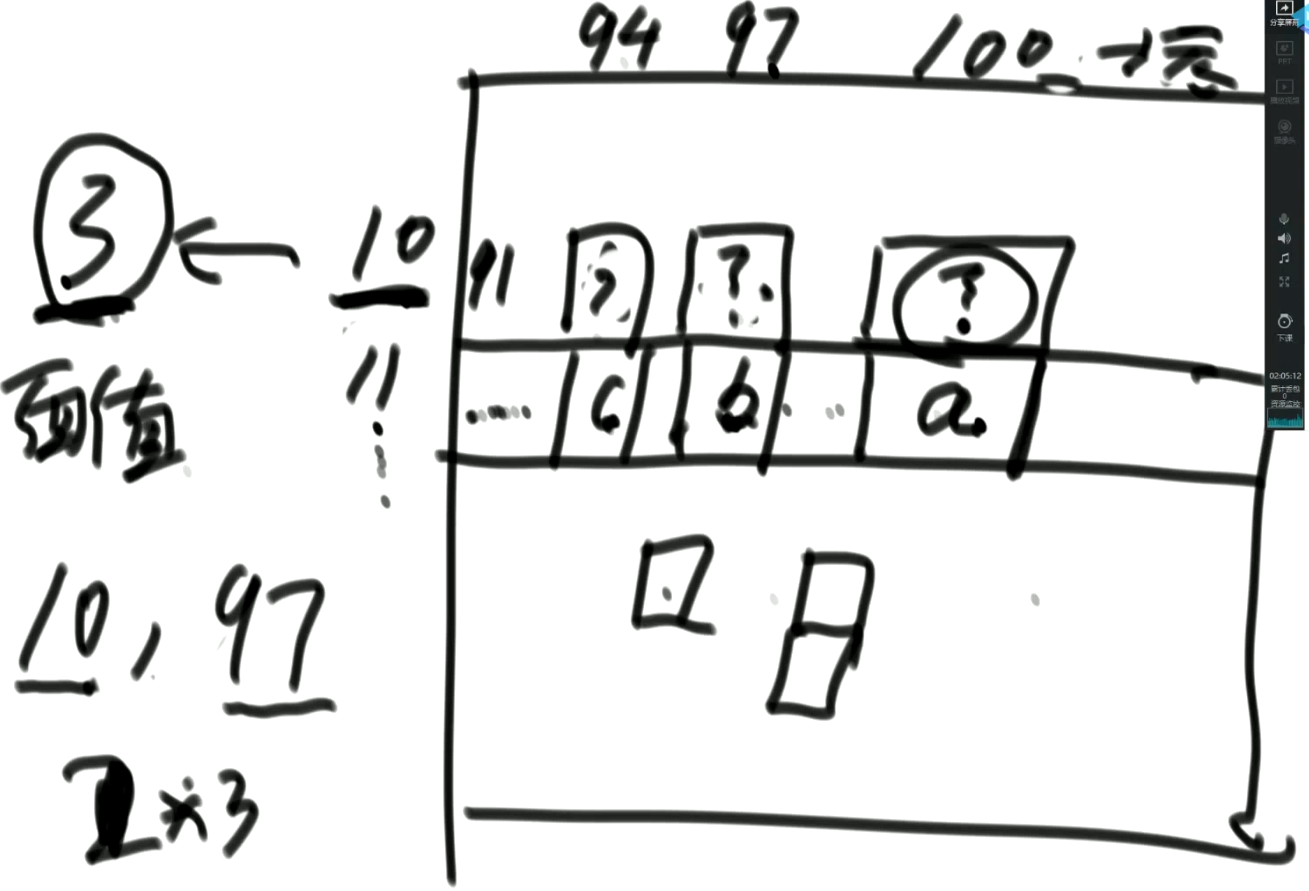
当前求从第10种货币开始,去凑齐100金额的情况总数,第10种货币面额为3。那么它等于以下情况的总和:
- 那么第10种货币可以选0张,就会变为求从第11种货币开始,去凑齐100金额的情况总数;
- 第10种选1张,变为求11种开始,凑齐97的情况总数;
- 第10种选2张,变为求11种开始,凑齐94的情况总数;
- …
而从第10中货币开始,凑齐97的方案总数为以下情况的和:
- 第10种选0张,变为求11种开始,凑齐97的情况总数;
- 第10种选1张,变为求11种开始,凑齐94的情况总数;
- 第10种选2张,变为求11种开始,凑齐91的情况总数;
- …
可见,求第10种货币开始,凑齐100金额的情况总数等于以下情况的和:
- 第10种选0张,变为求11种开始,凑齐100的情况总数;
- 第10种选1张,变为求10种开始,凑齐97的情况总数;
- 第10种选2张,变为求10种开始,凑齐94的情况总数;
- …
就可以利用已经求得的解,免去重复累加的过程。
在实际问题中,要做到优化枚举累加过程,可以尝试画出状态转换表,举出实际的例子,去尝试进行优化累加和过程。
-

记忆化搜索求解1:由于状态枚举的结果很多,所以没必要再弄成动态规划
// dp 傻缓存,如果t已经算过了,直接返回dp中的值 // t 剩余的目标 // 0..N每一个字符串所含字符的词频统计 // 返回值是-1,map 中的贴纸 怎么都无法rest public static int process1( HashMap<String, Integer> dp, int[][] map, String rest) { if (dp.containsKey(rest)) { return dp.get(rest); } // 以下就是正式的递归调用过程 int ans = Integer.MAX_VALUE; // ans -> 搞定rest,使用的最少的贴纸数量 int n = map.length; // N种贴纸 int[] tmap = new int[26]; // tmap 去替代 rest char[] target = rest.toCharArray(); for (char c : target) { tmap[c - 'a']++; } for (int i = 0; i < n; i++) { //判断当前帖纸能否剪切为目标字符串的第一个字符,贪心的去掉一些不必要的过程 if (map[i][target[0] - 'a'] == 0) { continue; } StringBuilder sb = new StringBuilder(); // i 贴纸, j 枚举a~z字符 for (int j = 0; j < 26; j++) { // if (tmap[j] > 0) { // j这个字符是target需要的 for (int k = 0; k < Math.max(0, tmap[j] - map[i][j]); k++) { sb.append((char) ('a' + j)); } } } // sb -> i String s = sb.toString(); int tmp = process1(dp, map, s); if (tmp != -1) { ans = Math.min(ans, 1 + tmp); } } // ans 系统最大 rest dp.put(rest, ans == Integer.MAX_VALUE ? -1 : ans); return dp.get(rest); }分析:
- 根据题意,最终需要剪切拼接的字符串每个字符的顺序没有要求,无论我们怎么拼接,只要最后将每个字符都有帖纸的字符来占位就行。
- 因此可以采用词频计数,来简化对字符串的操作。只要目标字符串中字符词频减去帖纸中的每个字母的词频,就可以当做当前目标字符串使用了该帖纸的一部分;
- 使用一个二维数组保存所有帖纸的词频数量,使用一个
HashMap<String, Integer>来缓存每个状态的解,使用rest代表要剪切的目标字符串。 - 当结果已经存在,就从缓存中直接拿;当使用给定的帖纸无论如何都剪切不成目标字符串时,返回-1.
- 搜索方法:尝试从每一个帖纸开始选取,然后用这个帖纸减去当前字符串,再进入下一步搜索。
- 其中需要注意,对于不能
- 本例子中对于词频的使用方法需要掌握。
-
最长公共子序列问题:
给定两个字符串,求出它们最长的公共子字符串长度:
s1 = "a1b23d"; s2 = "1nb23dj"; 则s1与s2的最长公共子序列为1b23d,长度为5分析,先从暴力搜索入手,搜索方法如下:
- 每一次搜索给定两个下标
i和j,表示搜索s1的前i个字符和s2的前j个字符的最长公共子序列; - Base Case为,
i == 0 && j == 0此时返回第0个字符是否相等即可。 - 当
i == 0 && j != 0时,只要s1的第1个字符和s2当前字符相等,那么最长子序列就是1,否则就搜索i=0,j=j-1的状态。j == 0 && i != 0时同理。 - 当
s1[i] == s2[j]时,最长公共子序列为1 +dfs(i-1,j-1)的情况; - 当
s1[i] != s2[j]时,最长公共子序列为dfs(i-1,j) dfs(i,j-1) dfs(i-1,j-1)中的最大者。不过dfs(i-1,j-1)可以忽略,前两种情况以及包含了它。
暴力搜索+记忆化
static int dfs(int i, int j, char[] s1, char[] s2, int[][] dp) { if(dp[i][j] != -1)return dp[i][j]; if(i == 0 && j == 0) { return dp[0][0] = s1[j] == s2[j] ? 1 : 0; } if(i == 0) { if(s1[0] != s2[j]) return dp[0][j] = dfs(0, j-1, s1, s2, dp); else return dp[0][j] = 1; } if(j == 0) { if(s2[0] != s1[i]) return dp[i][0] = dfs(i-1, 0, s1, s2, dp); else return dp[i][0] = 1; } int ans = 0; if(s1[i] == s2[j]) { ans = 1 + dfs(i-1,j-1,s1,s2, dp); }else { ans = Math.max(dfs(i-1,j,s1,s2, dp), dfs(i, j-1, s1, s2, dp)); } return dp[i][j] = ans; }优化为动态规划
static int plan(int[][] dp, char[] s1, char[] s2) { int ans = 0; dp[0][0] = s1[0] == s2[0] ? 1 : 0; for(int i = 1;i < s2.length;i++) { if(s1[0] == s2[i]) { dp[0][i] = 1; }else { dp[0][i] = dp[0][i-1]; } } for(int i = 1;i < s1.length;i++) { if(s1[i] == s2[0]) { dp[i][0] = 1; }else { dp[i][0] = dp[i-1][0]; } } for(int i = 1;i < s1.length;i++) { for(int j = 1;j < s2.length;j++) { if(s1[i] == s2[j]) { dp[i][j] = 1 + dp[i-1][j-1]; }else { dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]); } } } ans = dp[s1.length-1][s2.length-1]; return ans; } - 每一次搜索给定两个下标
2. 寻找业务限制的尝试模型
暴力搜索的状态可变范围不好寻找,需要结合具体的问题,去确定状态可变范围,才可以转变为动态规划。

暴力思路:前提,所给的喝完咖啡的时间是排好序的升序。
- 遍历每一杯咖啡,依次尝试当前这一杯是洗还是挥发更优。每一次遍历保存两个状态,当前杯子编号
index,下一次咖啡机可用的时间点washTime。 - Base Case设为,到达最后一杯咖啡的时候,最优解肯定是当前咖啡机可用时间和喝完咖啡的时间中较大者作为起始时间,然后比较洗杯子或者挥发杯子谁更优,返回。
- 当前杯子尝试洗杯子和挥发杯子两种方案,并且分别加上index之后的所有杯子干净的最早时间之和,然后返回更小的方案。需要注意洗杯子的情况下,需要增加
washTime的时间。
static int dfs(int[] arr, int a, int b, int washTime, int index) {
if(index == arr.length - 1) {
return Math.min(Math.max(arr[index], washTime) + a, arr[index] + b);
}
int wash = Math.max(arr[index], washTime) + a;
int next1 = dfs(arr, a, b, wash, index + 1);
int p1 = Math.max(wash, next1);
int dry = arr[index] + b;
int next2 = dfs(arr,a,b, washTime, index+1);
int p2 = Math.max(dry, next2);
return Math.min(p1, p2);
}
将其优化为动态规划,可以看出,搜索中的两个状态,index的范围是确定的,但是washTime的范围是不确定的,他可能会因为题目给出的范围不同而不同,这时,我们需要去求一个washTime极限值。也就是所有杯子都去由咖啡机清洗的最大时间。这就是需要根据业务的变化,去找动态规划的边界。
static int process(int[] arr,int[][] dp, int a, int b, int limit) {
if(a >= b)return arr[arr.length-1] + b;
for(int i = 0;i <= limit;i++) {
dp[arr.length-1][i] = Math.min(Math.max(arr[arr.length-1], i) + a, arr[arr.length-1] + b);
}
for(int i = arr.length-2;i >= 0;i--) {
for(int j = 0;j <= limit;j++) {
int wash = Math.max(arr[i], j) + a;
int p1 = Integer.MAX_VALUE;
if(wash <= limit)//防止数组越界
p1 = Math.max(wash, dp[i+1][wash]);
int dry = arr[i] + b;
int next2 = dp[i+1][j];
int p2 = Math.max(dry, next2);
dp[i][j] = Math.min(p1, p2);
}
}
return dp[0][0];
}
4. 动态规划的无后效性原则
所谓无后效性原则,指的是这样一种性质:某阶段的状态一旦确定,则此后过程的演变不再受此前各状态及决策的影响。也就是说,“未来与过去无关”,当前的状态是此前历史的一个完整总结,此前的历史只能通过当前的状态去影响过程未来的演变。具体地说,如果一个问题被划分各个阶段之后,阶段k中的状态只能通过阶段k+1中的状态通过状态转移方程得来,与其他状态没有关系,特别是与未发生的状态没有关系,这就是无后效性。 [2]
}
优化为动态规划
```java
static int plan(int[][] dp, char[] s1, char[] s2) {
int ans = 0;
dp[0][0] = s1[0] == s2[0] ? 1 : 0;
for(int i = 1;i < s2.length;i++) {
if(s1[0] == s2[i]) {
dp[0][i] = 1;
}else {
dp[0][i] = dp[0][i-1];
}
}
for(int i = 1;i < s1.length;i++) {
if(s1[i] == s2[0]) {
dp[i][0] = 1;
}else {
dp[i][0] = dp[i-1][0];
}
}
for(int i = 1;i < s1.length;i++) {
for(int j = 1;j < s2.length;j++) {
if(s1[i] == s2[j]) {
dp[i][j] = 1 + dp[i-1][j-1];
}else {
dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);
}
}
}
ans = dp[s1.length-1][s2.length-1];
return ans;
}
2. 寻找业务限制的尝试模型
暴力搜索的状态可变范围不好寻找,需要结合具体的问题,去确定状态可变范围,才可以转变为动态规划。
[外链图片转存中…(img-Ffyh68od-1644832363355)]
暴力思路:前提,所给的喝完咖啡的时间是排好序的升序。
- 遍历每一杯咖啡,依次尝试当前这一杯是洗还是挥发更优。每一次遍历保存两个状态,当前杯子编号
index,下一次咖啡机可用的时间点washTime。 - Base Case设为,到达最后一杯咖啡的时候,最优解肯定是当前咖啡机可用时间和喝完咖啡的时间中较大者作为起始时间,然后比较洗杯子或者挥发杯子谁更优,返回。
- 当前杯子尝试洗杯子和挥发杯子两种方案,并且分别加上index之后的所有杯子干净的最早时间之和,然后返回更小的方案。需要注意洗杯子的情况下,需要增加
washTime的时间。
static int dfs(int[] arr, int a, int b, int washTime, int index) {
if(index == arr.length - 1) {
return Math.min(Math.max(arr[index], washTime) + a, arr[index] + b);
}
int wash = Math.max(arr[index], washTime) + a;
int next1 = dfs(arr, a, b, wash, index + 1);
int p1 = Math.max(wash, next1);
int dry = arr[index] + b;
int next2 = dfs(arr,a,b, washTime, index+1);
int p2 = Math.max(dry, next2);
return Math.min(p1, p2);
}
将其优化为动态规划,可以看出,搜索中的两个状态,index的范围是确定的,但是washTime的范围是不确定的,他可能会因为题目给出的范围不同而不同,这时,我们需要去求一个washTime极限值。也就是所有杯子都去由咖啡机清洗的最大时间。这就是需要根据业务的变化,去找动态规划的边界。
static int process(int[] arr,int[][] dp, int a, int b, int limit) {
if(a >= b)return arr[arr.length-1] + b;
for(int i = 0;i <= limit;i++) {
dp[arr.length-1][i] = Math.min(Math.max(arr[arr.length-1], i) + a, arr[arr.length-1] + b);
}
for(int i = arr.length-2;i >= 0;i--) {
for(int j = 0;j <= limit;j++) {
int wash = Math.max(arr[i], j) + a;
int p1 = Integer.MAX_VALUE;
if(wash <= limit)//防止数组越界
p1 = Math.max(wash, dp[i+1][wash]);
int dry = arr[i] + b;
int next2 = dp[i+1][j];
int p2 = Math.max(dry, next2);
dp[i][j] = Math.min(p1, p2);
}
}
return dp[0][0];
}
4. 动态规划的无后效性原则
所谓无后效性原则,指的是这样一种性质:某阶段的状态一旦确定,则此后过程的演变不再受此前各状态及决策的影响。也就是说,“未来与过去无关”,当前的状态是此前历史的一个完整总结,此前的历史只能通过当前的状态去影响过程未来的演变。具体地说,如果一个问题被划分各个阶段之后,阶段k中的状态只能通过阶段k+1中的状态通过状态转移方程得来,与其他状态没有关系,特别是与未发生的状态没有关系,这就是无后效性。 [2]
对于不能划分阶段的问题,不能用动态规划来解;对于能划分阶段,但不符合最优化原理,也不能用动态规划来解;既能划分阶段,又符合最优化原理,但不具备无后效性原则的,还是不能用动态规划来解;误用动态规划程序设计方法求解会导致错误的结果。 [3]































 639
639











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








