5 分类:其他技术
目录
一、最近邻分类器
最近邻:和测试样例的属性相对接近的所有训练记录,称为(测试样例的)的最近邻。
利用最近邻可以对测试样例进行分类
最近邻分类器把每个样例看做d维空间上的一个数据点,其中d是属性个数。给定一个测试样例,利
用任意一种邻近性度量,计算该测试样例与训练集中其他数据点的邻近度。给定样例z的k-最近邻是指
和z距离最近的k个数据点.

k-最近邻分类算法

k值的选择 : 如果 k 太小, 则对噪声点敏感;如果 k 太大, 邻域可能包含很多其他类的点
定标问题(规范化):属性可能需要规范化,防止距离度量被具有很大值域的属性所左右
k-NN的特点
- 是一种基于实例的学习: 需要一个邻近性度量来确定实例间的相似性或距离
- 不需要建立模型,但分类一个测试样例开销很大: 需要计算与所有训练实例之间的距离
- 基于局部信息进行预测,对噪声非常敏感
- 最近邻分类器可以生成任意形状的决策边界: 决策树和基于规则的分类器通常是直线决策边界
- 需要适当的邻近性度量和数据预处理: 防止邻近性度量被某个属性左右
二、贝叶斯分类器
1)贝叶斯定理
对条件概率
P
(
Y
∣
X
)
、
P
(
X
∣
Y
)
P(Y|X)、 P(X|Y)
P(Y∣X)、P(X∣Y) ,有
- P ( X , Y ) = P ( Y ∣ X ) × P ( X ) = P ( X ∣ Y ) × P ( Y ) \color{red}P(X,Y)=P(Y|X) ×P(X)= P(X|Y) ×P(Y) P(X,Y)=P(Y∣X)×P(X)=P(X∣Y)×P(Y)
每个记录用一个
d
d
d维特征向量
X
=
(
x
1
,
x
2
,
…
,
x
d
)
X = (x_1, x_2, …, x_d)
X=(x1,x2,…,xd)表示
假定有
k
k
k个类
y
1
,
y
2
,
…
,
y
k
y_1, y_2, …, y_k
y1,y2,…,yk.
给定
X
,
X
X, X
X,X属于
y
j
y_j
yj 类的后验概率
P
(
y
j
∣
X
)
P(y_j|X)
P(yj∣X) 满足贝叶斯( Bayes)定理
- P ( y j , X ) = P ( X ∣ y j ) P ( y j ) P ( X ) \color{red}P(y_j,X)=\frac{P(X|y_j)P(y_j)}{P(X)} P(yj,X)=P(X)P(X∣yj)P(yj)
M A P MAP MAP (最大后验假设)
- 将X指派到具有最大后验概率 P ( y j ∣ X ) P(y_j|X) P(yj∣X)的类 y j y_j yj,即 将 X X X指派到 P ( X ∣ y j ) P ( y j ) P(X|y_j)P(y_j) P(X∣yj)P(yj) 最大的类 y j y_j yj
2)贝叶斯定理在分类中的应用
后验概率:
- P ( Y ∣ X ) = P ( X ∣ Y ) P ( Y ) P ( X ) \color{red}P(Y|X)=\frac{P(X|Y)P(Y)}{P(X)} P(Y∣X)=P(X)P(X∣Y)P(Y)
在比较不同 Y Y Y值的后验概率时:
- 分母 P ( X ) P(X) P(X)总是常数, 因此可以忽略 。
- 先 验 概 率 P ( Y ) \color{BLUE}先验概率P(Y) 先验概率P(Y)可以通过计算训练集中属于每一个类的训练样本所占的比例容易地估计。
- 对于类条件概率 P ( X ∣ Y ) P(X|Y) P(X∣Y)的估计比较麻烦。
根据类条件概率 P ( X ∣ Y ) P(X|Y) P(X∣Y)的估计方法不同,贝叶斯分类的不同实现方法包括: 朴素贝叶斯分类 、贝叶斯信念网络
3)朴素贝叶斯分类

估计
P
(
y
j
)
P(y_j)
P(yj)
- 类 y j y_j yj 的先验概率可以用下式估计 P ( y j ) = n j / n P(y_j )=n_j/n P(yj)=nj/n
- 其中, n j n_j nj 是类 y j y_j yj 中的训练样本数,而 n n n是训练样本总数
估计 P ( X ∣ y j ) P(X|y_j) P(X∣yj)
- 为便于估计 P ( X ∣ y j ) P(X|y_j ) P(X∣yj), 假定类条件独立----给定样本的类标号, 假定属性值条件地相互独立.
- 于是,
P
(
X
∣
Y
=
y
j
)
P(X|Y=y_j)
P(X∣Y=yj)可以用下式估计
P ( X ∣ y j ) = ∏ i = 1 d P ( x i ∣ y j ) \color{red}P(X|y_j)=\displaystyle\prod_{i=1}^{d} {P(x_i|y_j)} P(X∣yj)=i=1∏dP(xi∣yj) - 其中, P ( x i ∣ y j ) P(x_i |y_j) P(xi∣yj)可以由训练样本估值
估计 P ( x i ∣ y j ) P(x_i |y_j) P(xi∣yj)
- 设第
i
i
i个属性
A
i
A_i
Ai 是分类属性, 则
P
(
x
i
∣
y
j
)
=
n
i
j
/
n
j
P(x_i|y_j ) = n_{ij}/n_j
P(xi∣yj)=nij/nj
其中 n i j n_{ij} nij是在属性 A i A_i Ai 上具有值 x i x_i xi的 y j y_j yj 类的训练样本数, 而 n j n_j nj是 y j y_j yj 类的训练样本数 - 设第
i
i
i个属性
A
i
A_i
Ai 是连续值属性
把 A i A_i Ai 离散化
假定 A i A_i Ai服从高斯分布
P ( x i ∣ y j ) = 1 2 π σ i j e − ( x i − μ i j ) 2 2 σ i j 2 \color{red}P(x_i|y_j)=\frac{1}{\sqrt {2π}\sigma_{ij}}e^{-\frac{(x_i-\mu_{ij})^2}{2\sigma_{ij}^2}} P(xi∣yj)=2πσij1e−2σij2(xi−μij)2
其中, μ i j \mu_{ij} μij, σ i j \sigma_{ij} σij分别为给定 y j y_j yj 类的训练样本在属性 A i A_i Ai 上的均值和标准差
朴素贝叶斯分类器所需要的信息(计算步骤)
- 计算每个类的先验概率
P
(
y
j
)
P(y_j)
P(yj)
P
(
y
j
)
=
n
j
/
n
P(y_j )=n_j/n
P(yj)=nj/n
其中, n j n_j nj是 y i y_i yi 类的训练样本数,而 n n n是训练样本总数 - 对于离散属性
A
i
A_i
Ai,设的不同值为
a
i
1
,
a
i
2
,
…
,
a
i
l
a_{i1}, a_{i2}, …,a_{il}
ai1,ai2,…,ail ,
对于每个类 y j y_j yj,计算后验概率 P ( a i k ∣ y j ) , 1 ≤ k ≤ l P(a_{ik}|y_j ), 1\le k\le l P(aik∣yj),1≤k≤l P ( a i k ∣ y j ) = n i k j / n j P(a_{ik}|y_j )= n_{ikj}/n_j P(aik∣yj)=nikj/nj
其中 n i k j n_{ikj} nikj 是在属性 A i A_i Ai上具有值 a i k a_{ik} aik的 y j y_j yj 类的训练样本数, 而 n j n_j nj是 y j y_j yj 类的训练样本数 - 对于连续属性 A i A_i Ai 和每个类 y j y_j yj,计算 y j y_j yj 类样本的均值 μ i j \mu_{ij} μij,标准差 σ i j \sigma_{ij} σij。利用高斯分布估计 P ( x i ∣ y j ) P(x_i |y_j) P(xi∣yj)


朴素贝叶斯分类的特点
- 对孤立的噪声点的鲁棒性
个别点对概率估计的影响很小 - 容易处理缺失值
在估计概率时忽略缺失值的训练实例 - 对不相关属性的鲁棒性
各类在不相关属性上具有类似分布 - 类条件独立假设可能不成立
使用其他技术,如贝叶斯信念网络BBN
三、支持向量机SVM
支持向量机SVM
优点:
- 对复杂的非线性边界的建模能力
- 与其它模型相比, 它们不太容易过分拟合
- 支持向量机还提供了学习模型的紧凑表示
- 广泛的使用范围:
SVM可以用来预测和分类
它们已经用在许多领域, 包括手写数字识别、对象识别、演说人识别
两个线性可分的类
- 找到这样一个超平面,使得所有的方块位于这个超平面的一侧,而所有的圆圈位于它的另一侧
- 可能存在无穷多个那样的超平面
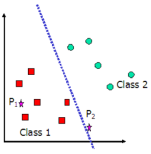
决策边界的边缘
“最大边缘”原理:
即追求分类器的泛化能力最大化。即希望所找到的决策边界,在满足将两类数据点正确的分开的前提下,对应的分类器边缘最大。这样可以使得新的测试数据被错分的几率尽可能小。
如下图所示的情况(b)就比情况(a)的泛化能力强,其原因在于其分界面与两类样本中的最近的样本的距离最大.

SVM的决策边界和边缘
一个线性分类器的决策边界可以写成如下形式:
w
x
+
b
=
0
wx + b = 0
wx+b=0 其中,
w
w
w 和
b
b
b 是模型的参数
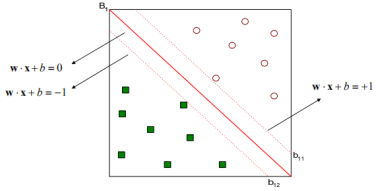
边缘
方块的类标号为
+
1
+1
+1,圆圈的类标号为
−
1
-1
−1
z
z
z的类标号
y
y
y
y
=
{
1
,
if
w
⋅
z
≥
0
−
1
,
if
w
⋅
z
<
0
y= \begin{cases} 1, & \text {if $w \cdot z\geq0$} \\ -1, & \text{if $w \cdot z<0$} \end{cases}
y={1,−1,if w⋅z≥0if w⋅z<0
调整决策边界的参数
w
w
w 和
b
b
b,两个平行的超平面
b
i
1
b_{i1}
bi1和
b
i
2
b_{i2}
bi2可以表示如下
b
i
1
:
w
x
+
b
=
1
b_{i1}:w x + b = 1
bi1:wx+b=1
b
i
2
:
w
x
+
b
=
−
1
b_{i2}:w x + b = -1
bi2:wx+b=−1
可以证明, 边缘
d
d
d
d
=
2
∣
∣
w
∣
∣
d=\frac{2}{||w||}
d=∣∣w∣∣2
边缘推导
w
w
w的方向垂直于决策边界
- 如果 x a x_a xa 和 x b x_b xb 是任意两个位于决策边界上的点,则 w x a + b = 0 , w x b + b = 0 wx_a + b = 0, wx_b + b = 0 wxa+b=0,wxb+b=0
- 于是 w ( x b − x a ) = 0 w(x_b - x_a) =0 w(xb−xa)=0. 由于 x b − x a x_b -x_a xb−xa是决策超平面中任意向量,于是 w w w的方向必然垂直于决策边界
令
x
1
x_1
x1是
b
i
1
b_{i1}
bi1上的数据点,
x
2
x_2
x2是
b
i
2
b_{i2}
bi2上的数据点. 代入
b
i
1
b_{i1}
bi1和
b
i
2
b_{i2}
bi2相减得到
w
.
(
x
1
−
x
2
)
=
2
w.(x_1 - x_2) = 2
w.(x1−x2)=2
由
c
o
s
(
u
,
v
)
=
u
⋅
v
∣
∣
u
∣
∣
∣
∣
v
∣
∣
cos(u,v)=\frac{u \cdot v}{||u||||v||}
cos(u,v)=∣∣u∣∣∣∣v∣∣u⋅v ,即
u
⋅
v
=
∣
∣
u
∣
∣
∣
∣
v
∣
∣
c
o
s
(
u
,
v
)
u \cdot v=||u||||v||cos(u,v)
u⋅v=∣∣u∣∣∣∣v∣∣cos(u,v)
令
u
=
w
,
v
=
x
1
−
x
2
u=w, v= x1 - x2
u=w,v=x1−x2, 得到
∣
∣
w
∣
∣
∣
∣
x
1
−
x
2
∣
∣
c
o
s
(
w
,
x
1
−
x
2
)
=
2
||w|||| x1-x2 ||cos(w, x1 - x2)=2
∣∣w∣∣∣∣x1−x2∣∣cos(w,x1−x2)=2
但
∣
∣
x
1
−
x
2
∣
∣
c
o
s
(
w
,
x
1
−
x
2
)
=
d
|| x1 - x2 ||cos(w, x1 - x2)=d
∣∣x1−x2∣∣cos(w,x1−x2)=d
于是
∣
∣
w
∣
∣
×
d
=
2
||w||×d=2
∣∣w∣∣×d=2,即
d
=
2
∣
∣
w
∣
∣
d=\frac{2}{||w||}
d=∣∣w∣∣2
1)SVM
SVM的训练阶段从训练数据中估计决策边界的参数
w
w
w 和
b
b
b 最大化边缘
d
d
d,并满足
w
x
i
+
b
≥
1
,
如
果
y
i
=
1
wx_i + b≥1 ,如果y_i = 1
wxi+b≥1,如果yi=1
w
x
i
+
b
≤
−
1
,
如
果
y
i
=
−
1
wx_i + b≤-1 ,如果y_i = -1
wxi+b≤−1,如果yi=−1
即
y
i
(
w
x
i
+
b
)
≥
1
y_i(wx_i + b)≥1
yi(wxi+b)≥1
最大化
d
d
d等价于最小化
m
i
n
1
2
∣
∣
w
∣
∣
2
约
束
条
件
y
i
(
w
x
i
+
b
)
≥
1
,
i
=
1
,
2
,
.
.
.
,
N
min\frac{1}{2}||w||^2\\ 约束条件 y_i( wx_i+b)≥1, i=1,2,..., N
min21∣∣w∣∣2约束条件yi(wxi+b)≥1,i=1,2,...,N
这是一个凸二次优化问题,可以通过标准的拉格朗日乘子方法求解



2)不可分情况:软边缘SVM
对于许多实际问题,前面讨论的最优决策超平面的条件
y
i
g
(
x
i
)
=
y
i
(
w
T
x
i
−
b
)
≥
1
,
i
=
1
,
2
,
…
n
y_ig(x_i)=y_i(w^Tx_i-b)≥1 , i=1,2,…n
yig(xi)=yi(wTxi−b)≥1,i=1,2,…n
过于严格。
◇ 对存在数据污染、近似线性分类的情况,可能并不存在一个最优的线性决策超平面
◇ 存在噪声数据时,为保证所有训练数据的准确分类,可能会导致过拟合



软边缘(soft margin)SVM的基本工作原理:
对存在数据污染、近似线性分类的情况,可能并不存在一个最优的线性决策超平面;当存在噪声数据时,为保证所有训练数据的准确分类,可能会导致过拟合。因此,需要允许有一定程度“错分”,又有较大分界区域的最优决策超平面,即软间隔支持向量机。
软间隔支持向量机通过引入松弛变量、惩罚因子,在一定程度上允许错误分类样本,以增大间隔距离。在分类准确性与泛化能力上寻求一个平衡点。
3)非线性SVM




非线性支持向量机的基本工作原理
对非线性可分的问题,可以利用核变换,把原样本映射到某个高维特征空间,使得原本在低维特征空间中非线性可分的样本,在新的高维特征空间中变得线性可分,并使用线性支持向量机进行分类。

SVM的特点
SVM学习问题可以表示为凸优化问题,因此可以利用已知的有效算法发现目标函数的全局最小值
SVM通过最大化决策边界的边缘来控制模型的能力
- 需要提供其他参数,如使用的核函数类型、为了引入松弛变量所需的代价函数C等
分类属性处理
- 每个分类属性值引入一个哑变量, 转化为二元变量
- 例如,如果婚姻状况有3个值{单身,已婚,离异},可以对每一个属性值引入一个二元变量
可以推广到多类问题
多类问题
SVM是对二类问题设计的;还有一些方法也是针对二类问题的;如何处理多类问题?
训练
令
Y
=
y
1
,
y
2
,
.
.
.
,
y
K
Y = {y_1, y_2,..., y_K}
Y=y1,y2,...,yK是类标号的集合
1
−
r
1-r
1−r方法 : 分解成
K
K
K个二类问题
- 每一个类 y i ∈ Y y_i\in Y yi∈Y创建一个二类问题, 其中所有属于 y i y_i yi的样本都被看作正类, 而其他样本作为负类
1 − 1 1-1 1−1方法 : 构建 K ( K − 1 ) / 2 K(K-1)/2 K(K−1)/2个二类分类器
- 每一个分类器用来区分一对类 ( y i , y j ) (y_i, y_j) (yi,yj)
- 为类 ( y i , y j ) (y_i, y_j) (yi,yj) 构建二类分类器时, 不属于 y i y_i yi或 y j y_j yj的样本被忽略掉
四、人工神经网络ANN

神经元是由细胞体,树突和轴突三部分组成。
树突是接受从其它神经元传入的信息的入口。
轴突是把神经元兴奋的信息传出到其它神经元的出口。
当神经元接受来自其它神经元的信息时,膜电位在开始时是按时间连续渐渐变化的。
当膜电位变化经超出一个定值时,才产生突变上升的脉冲,这个脉冲接着沿轴突进行传递。神经元这种膜电位高达一定阀值才产生脉冲传送的特性称阀值特性。
从神经元的特性和功能可以知道,神经元是一个多输入单输出的信息处理单元,而且,它对信息的处理是非线性的。
根据神经元的特性和功能,可以把神经元抽象为一个简单的数学模型。
人工神经网络——感知器
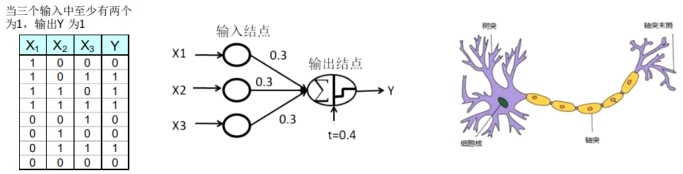
感知器模型的输出可以由此公式计算:
Y
=
s
i
g
n
(
∑
i
w
i
X
i
−
t
)
Y=sign(\displaystyle\sum_{i}^{} w_iX_i-t)
Y=sign(i∑wiXi−t)
Y
=
s
i
g
n
(
0.3
X
1
+
0.3
X
2
+
0.3
X
3
−
0.4
)
w
h
e
r
e
s
i
g
n
(
z
)
=
{
1
,
if
z
>
0
0
,
if
z
≤
0
Y = sign(0.3 X_1 + 0.3X_2 +0.3X_3 -0.4)\\ where \ \ \ sign(z) = \begin{cases} 1, & \text {if $z>0$ } \\ 0, & \text{if $z≤0$ } \end{cases}
Y=sign(0.3X1+0.3X2+0.3X3−0.4)where sign(z)={1,0,if z>0 if z≤0
多层人工神经网络
多层人工神经网络包括: 输入层、隐藏层(可以有多个)、输出层。

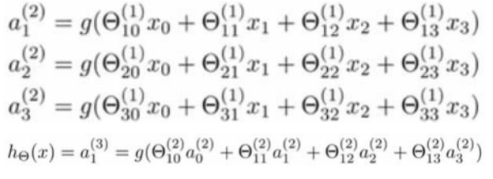
人工神经网络中的激活函数


Logistic回归
l
o
g
i
s
t
i
c
logistic
logistic 回归问题是构造一个只含有输入层和输出层的神经网络,其结构图如下:
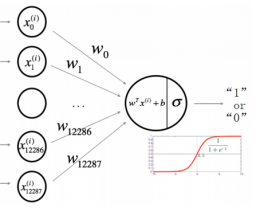
分类问题的一般描述:
- 用 X X X代表输入空间,是输入向量的所有可能取值的集合,也叫特征空间; Y Y Y代表输出空间,是输出的所有可能取值的集合。
- x ( i ) ∈ X x(i)∈X x(i)∈X代表特征空间的一个样本, y ( i ) ∈ Y y(i)∈Y y(i)∈Y代表其类别(标签)。
- 分类问题的一般描述可总结为:利用已知标签的训练集 X t r a i n X_{train} Xtrain训练出一个模型,该模型包含一个映射关系 h : X → Y h:X→Y h:X→Y, h h h应该能够对新的数据点 x ( m + 1 ) x^{(m+1)} x(m+1)预测其类别 y ( m + 1 ) y^{(m+1)} y(m+1),并使得预测结果的正确率尽可能高。
L o g i s t i c Logistic Logistic 回归问题的描述:
- 以二分类问题为例,用0和1代表可能的类别Y={0,1}。
- 给定输入特征向量 x x x,希望估计出它属于两类的概率 P ( y = 0 ∣ x ; θ ) P(y=0|x;\theta) P(y=0∣x;θ)和 P ( y = 1 ∣ x ; θ ) P(y=1|x;\theta) P(y=1∣x;θ)。令 y ^ = P ( y = 1 ∣ x ; θ ) \hat y=P(y=1|x;\theta) y^=P(y=1∣x;θ)
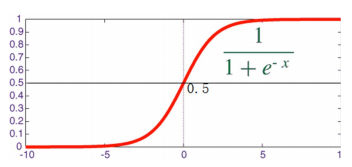
- 为估计 y ^ \hat y y^,最简单的方法就是令 y ^ = w T x + b \hat y=w^Tx+b y^=wTx+b 。但这样可能会导致 y ^ \hat y y^ 的值大于1或者小于0,不符合概率的要求。可以在线性回归的表达式前面加上 s i g m o i d sigmoid sigmoid函数,即 y ^ = σ ( w T x + b ) \hat y=\sigma(w^Tx+b) y^=σ(wTx+b)
-
s
i
g
m
o
i
d
sigmoid
sigmoid 函数的表达式:
σ
(
z
)
=
1
1
+
e
−
z
\sigma(z)=\frac{1}{1+e^{-z}}
σ(z)=1+e−z1 或
g
(
z
)
=
1
1
+
e
−
z
g(z)=\frac{1}{1+e^{-z}}
g(z)=1+e−z1
损失函数的选取:
- 一种很自然的想法是选取 L ( y ^ , y ) = 1 2 ( ( y ^ − y ) 2 ) L(\hat y,y)=\frac{1}{2}((\hat y-y)^2) L(y^,y)=21((y^−y)2) 作为损失函数,但这不是一个凸优化问题。
- 定义单个样本的损失函数为
L
(
y
^
,
y
)
=
−
(
y
l
n
(
y
^
)
+
(
1
−
y
)
l
n
(
1
−
y
^
)
)
L(\hat y,y)= -(yln(\hat y) + (1-y)ln(1-\hat y))
L(y^,y)=−(yln(y^)+(1−y)ln(1−y^))
当y=1, L ( y ^ , y ) = − l n ( y ^ ) L(\hat y,y)= -ln(\hat y) L(y^,y)=−ln(y^) , L ( y ^ , y ) L(\hat y,y) L(y^,y) 为单调递减函数, y ^ \hat y y^越大,损失函数 L ( y ^ , y ) L(\hat y,y) L(y^,y) 越小
当y=0, L ( y ^ , y ) = − l n ( 1 − y ^ ) L(\hat y,y)= -ln(1-\hat y) L(y^,y)=−ln(1−y^) , L ( y ^ , y ) L(\hat y,y) L(y^,y) 为单调递增函数, y ^ \hat y y^越大,损失函数 L ( y ^ , y ) L(\hat y,y) L(y^,y) 越大
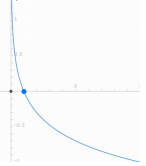
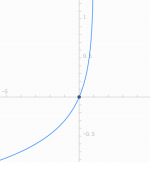
损失函数:
- 定义单个样本的损失函数为
L
(
y
^
,
y
)
=
−
(
y
l
n
(
y
^
)
+
(
1
−
y
)
l
n
(
1
−
y
^
)
)
L(\hat y,y)= -(yln(\hat y) + (1-y)ln(1-\hat y))
L(y^,y)=−(yln(y^)+(1−y)ln(1−y^))
y ^ = σ ( w T x + b ) \hat y=\sigma(w^Tx+b) y^=σ(wTx+b) , σ ( z ) = 1 1 + e − z \sigma(z)=\frac{1}{1+e^{-z}} σ(z)=1+e−z1 - 样本总体的代价函数
J
(
w
,
b
)
J(w,b)
J(w,b)最小化
J ( w , b ) = − 1 m ∑ i = 1 m ( y ( i ) l n ( y ^ ( i ) ) + ( 1 − y ( i ) ) l n ( 1 − y ^ ( i ) ) ) J(w,b)=-\frac{1}{m}\sum_{i=1}^{m}(y^{(i)}ln(\hat y^{(i)})+(1-y^{(i)})ln(1-\hat y^{(i)})) J(w,b)=−m1i=1∑m(y(i)ln(y^(i))+(1−y(i))ln(1−y^(i)))
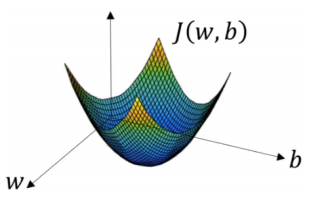
梯度下降法:
- 先随机在曲面上找一个点,然后求出该点的梯度,然后顺着这个梯度的方向往下走一步,到达一个新的点之后,重复以上步骤,直到到达最低点(或达到迭代终止条件)

五、不平衡类问题
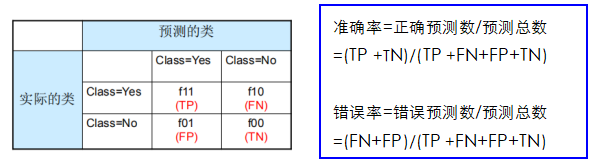
准确率的缺点 :
- 考虑一个两类问题
类0的样本数 = 9990 类1的样本数 = 10 - 如果模型预测所有的样本为类0, 准确率为 9990/10000 = 99.9 %
准确率的值具有欺骗性 ;模型并没有分对类1的任何样本
可选度量
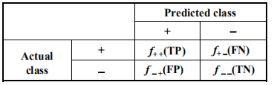
混淆矩阵
真正率(true positive rate, TPR)或灵敏度(sensitivity) TPR = TP/(TP + FN)
真负率(ture negative rate, TNR)或特指度(specificity) TNR = TN/(TN + FP)
假正率(false positive rate, FPR) FPR = FP/(TN + FP)
假负率(false negative rate, FNR) FNR = FN/(TP + FN)
召回率(recall) recall=TP/(TP + FN)
精度(precision) precision=TP/(TP + FP)
F1度量 :
F
1
=
2
r
p
r
+
p
=
2
×
T
P
2
×
T
P
+
F
P
+
F
N
F_1=\frac{2rp}{r+p}=\frac{2×TP}{2×TP+FP+FN}
F1=r+p2rp=2×TP+FP+FN2×TP
召回率
召回率度量被分类器正确预测的正样本的比例。具有高召回率的分类器很少将正样本误分为负样本。
recall=TP/(TP + FN)=TP/所有正样本数目
真正率(TPR)——灵敏度(sensitivity)——召回率(recall)
精度
精度(precision)确定在分类器断言为正类的那部 分记录中实际为正类的记录所占的比例。
precision=TP/(TP + FP)=TP/标记为正样本的数目
接受者操作特性曲线ROC
接受者操作特性曲线(Receiver Operating Characteristic, ROC)是显示分类器真正率(TPR)和假正率(FPR)之间 折中的一种图形化方法。
- 纵轴:真正率(TPR) TPR = TP/(TP + FN) =TP/所有正样本数目
- 横轴:假正率(FPR) FPR = FP/(TN + FP) =FP/所有负样本数目
接受者操作特性曲线(ROC)
ROC 曲线上有几个关键点,它们有公认的解释:
- (TPR=0,FPR=0):把每个实例都预测为负类的模型
- (TPR=1,FPR=1):把每个实例都预测为正类的模型
- (TPR=1,FPR=0):理想模型
ROC 曲线有助于比较不同分类器的相对性能



bingo~ ✨ 世上有的是比你了不起的人。了不起需要与生俱来,但活得好是事在人为。
























 8942
8942











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








