(图)最短路径之弗洛伊德算法

弗洛伊德Floyd算法：

其本质是动态规划算法，也是经典的多源最短路径算法

之所以称为经典便是因为该算法非常简短：

该算法的时间复杂度：O(n的三次方)

这个算法短的离谱,以致于我们通常直接将它背了下来当模板使用,而不像学dijkstra那时候一步步理解它是如何贪心的.

那么,为什么floyd算法是这个样子的呢?或者说,为什么这样就能求出所有点到所有点的最短路径?

它的递推公式是：

D[v][w]=min{D[v][w],D[v][k]+D[k][w]}

接下来详细探究Floyd：

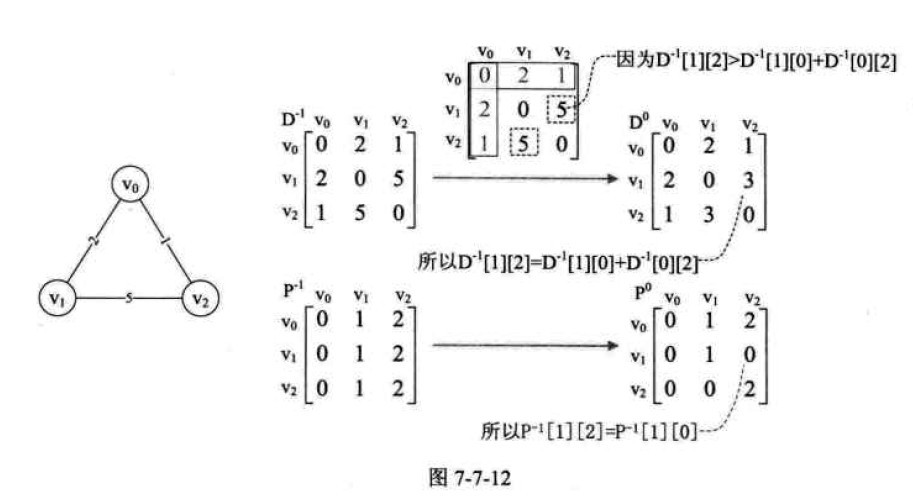
D代表的是顶点到顶点的最短路径权值和的矩阵   初始化D-1

P代表对应顶点的最小路径的前驱矩阵                初始化P-1

然后分析所有经过V0顶点后到达另一顶点的最短路径。V1->V0->V2,有D-1[1][0]+D-1[0][2]=2+1=3,D-1[1][2]表示V1->V2的权值是5，3<5,根据递推公式，D的0次方[1][2]的值更新为3，同样的，D[2][1]=3

P的0次方也有变化，即前驱结点改变了。之后的操作同前面一样。

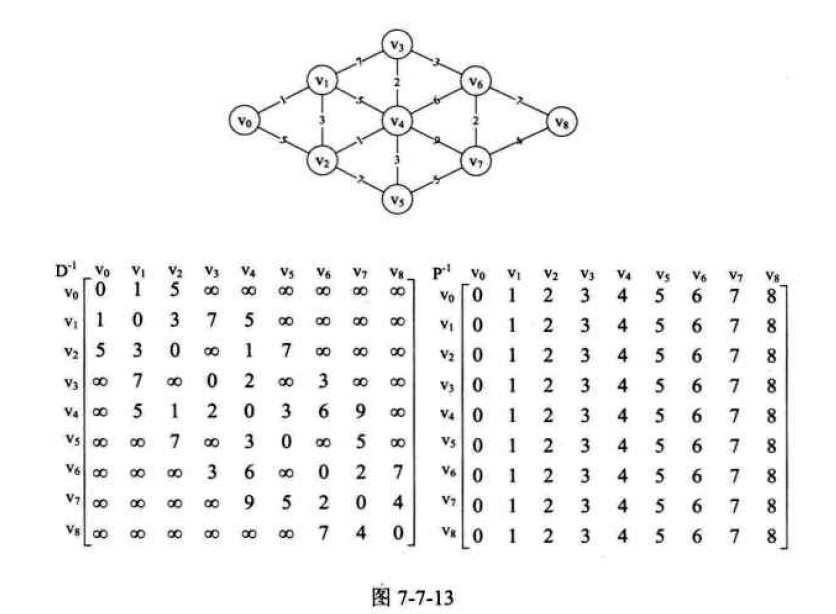
对于复杂一些的图而言，算法核心内容不变：

D存储顶点间的权值和，P存储最短路径

代码如下：

typedef int Path[MAX][MAX]                
typedef int ShortPath[MAX][MAX] 
        
void ShortPath_Floyd(MGraph G,Path *p,ShortPath *D)
{
	int v,w,k;
	for(v=0;v<G.numVertexes;v++)
	{
		for(w=0;w<G.numVertexes;w++)
		{
			(*D)[v][w]=G.arc[v][w];		//将原邻接矩阵的对应值，即各边的权值存入D数组 
			(*p)[v][w]=w;            	//初始化p 
		}
	}
	for(k=0;k<G.numVertexes;k++)	 //k一定要放在最外层循环 
	{
		for(v=0;v<G.numVertexes;v++) 
		{
			for(w=0;w<G.numVertexes;w++) 
			{
				if((*D)[v][w]>(*D)[v][k]+(*D)[k][w]) //递推条件
				{
					(*D)[v][w]=(*D)[v][k]+(*D)[k][w];
					(*p)[v][w]=(*p)[v][k];            //路径设置为经过下标k的顶点，即前驱是k 
				}
			}
		}	
	}		
 } 

特变要注意的是第15行代码：K一定要放在最外层循环！！

证明如下：

有一个致命的结论：

假设i和j之间的最短路径上的结点集里(不包含i,j),编号最大的一个是x.那么在外循环k=x时,d[i][j]肯定得到了最小值.

故K需要放在最外层

假如k在最里层,那么d[i][j]=min(d[i][j],d[i][k]+d[k][j])是一次性执行完.

那么我们就要保证,在这时候,至少存在一个k=x,使得d[i][x]和d[x][j]都是取得了最小值.

然而在这种情况下我们并不能保证,但如果k在最外层就可以保证了.

至于v，w的次序倒是随意，不影响算法实现。