在数论,对正整数n,欧拉函数是小于或等于 n 的数中与 n 互素的数的数目。
若 m,n互素,那么
证明:
构造如图所示的矩阵,恰好包含 mn 个数。
则 phi(mn)是上述数字矩阵中与 mn 互素的数的个数,也就是与 m、n 同时互素的数的个数(由于m与n互素)。
由于 GCD(km+r,m)=GCD(r, m),所以每一列的 n 个元素同时与 m 互素当且仅当 GCD(r,m)=1,因此与 m互素的列共有phi(m)列
假定第 r 列元素满足GCD(r,m)=1. 则该列的所有元素为
而这些元素恰好构成模 n完全剩余系,所以其中恰有 phi(n) 个与 n 互素的数
综上:上述数字矩阵中与 m 互素的列共有 phi(m) 列,每个这样的列当中恰有 phi(n) 个与 n互素的数,所以总共与 mn 互素的数的个数为 phi(m) phi(n)
故








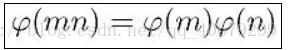

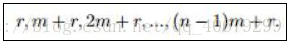














 1310
1310











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








