核技巧（Kernel Trick）与支持向量回归（SVR）详解

核技巧（Kernel Trick）与支持向量回归（SVR）详解

第十五次写博客，本人数学基础不是太好，如果有幸能得到读者指正，感激不尽，希望能借此机会向大家学习。这一篇内容来自于《机器学习》和林轩田《技法》以及自己的一些理解。

这篇文章首先对表示定理（Representor Theorem）进行介绍和证明，然后引出核技巧（Kernel Trick）及其应用，再介绍核技巧版的线性回归即核线性回归，最后通过核线性回归和带核SVM对比引出支持向量回归（Support Vector Regression）。

表示定理（Representor Theorem）

  令$\mathbf{H}$为核函数$k$对应的再生核希尔伯特空间（Mercer 定理中提到过），$||h|{|}_{\mathbf{H}}$表示$\mathbf{H}$空间中关于优化问题的解$h$的范数，对于任意单调递增函数$\Omega :[0,\infty ]\mapsto \mathbb{R}$和任意非负损失函数$l:{\mathbb{R}}^m\mapsto [0,\infty ]$，优化问题

的解总可写为

  表示定理对损失函数没有限制，对正则化项$\Omega$仅要求单调递增，甚至不要求$\Omega$是凸函数，因此对于一般的损失函数和正则化项，优化问题的最优解$h^{\ast }\left(\mathbf{x}\right)$都可以表示为核函数$k\left(\mathbf{x},{\mathbf{x}}_i\right)$的线性组合。
  下面以带有$L_2$正则项的线性模型为例，证明这个定理，假设该优化问题可以表示为

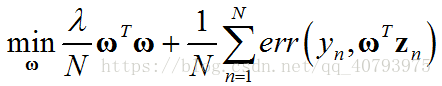
其中，${\mathbf{z}}_n=\varphi \left({\mathbf{x}}_n\right)$，假设该问题的最优解为

最优的目标变量可以写为

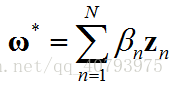
  证明上式成立，目标变量的一般形式可以写为${\omega }^{\ast }={\omega }_{||}+{\omega }_{\perp }$，其中，${\omega }_{||}\in span\left({\mathbf{x}}_n\right)$，${\omega }_{\perp }\perp span\left({\mathbf{x}}_n\right)$，为了得到形如上式的最优解，应该使垂直分量${\omega }_{\perp }=0$。根据反证法，如果该分量不为零，那么优化目标中的第二项，由于${\omega }_{\perp }\perp span\left({\mathbf{x}}_n\right)$的原因，可以表示为