机器学习与深度学习核心知识点总结–写在校园招聘即将开始时
数学–CVer
理解梯度下降法–SIGAI
激活函数
- sigmoid
f ( x ) = 1 1 + e − x f(x)=\frac{1}{1+e^{-x}} f(x)=1+e−x1
sigmoid求导: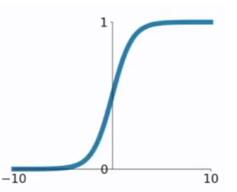
f ′ ( x ) = ( 1 1 + e − x ) ′ = e − x ( 1 + e − x ) 2 = f ( x ) ( 1 − f ( x ) ) f'(x) = (\frac{1}{1+e^{-x}})' = \frac{e^{-x}}{(1+e^{-x})^2}=f(x)(1-f(x)) f′(x)=(1+e−x1)′=(1+e−x)2e−x=f(x)(1−f(x))
sigmoid函数作为非线性激活函数,但是其并不被经常使用,它具有以下几个缺点:- 当 x x x值非常大或者非常小时,通过上图我们可以看到,sigmoid函数的导数 f ′ ( x ) f^′(x) f′(x) 将接近 0 。这会导致权重 W W W 的梯度将接近 0 ,使得梯度更新十分缓慢,甚至发生梯度消失;
- sigmoid 函数的输出不是以0为均值,不便于下一层的计算;
sigmoid函数可用在网络最后一层,作为输出层进行二分类,尽量不要使用在隐藏层。
- tanh函数
tanh函数将取值为 ( − ∞ , + ∞ ) (−∞,+∞) (−∞,+∞) 的数映射到 ( − 1 , 1 ) (−1,1) (−1,1) 之间:
f ( x ) = e x − e − x e x + e − x f(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}} f(x)=ex+e−xex−e−x
tanh 求导: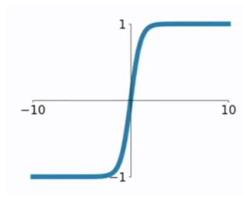
f ′ ( x ) = ( e x − e − x e x + e − x ) ′ = 4 ( e x + e − x ) 2 = 1 − f 2 ( x ) f'(x)=(\frac{e^x-e^{-x}}{e^x+e^{-x}})^{'}=\frac{4}{(e^x+e^{-x})^2}=1-f^2(x) f′(x)=(ex+e−xex−e−x)′=(ex+e−x)24=1−f2(x)
tanh函数在 0 附近很短一段区域内可看做线性的。由于tanh函数均值为 0 ,因此弥补了sigmoid函数均值为 0.5 的缺点,但是当 x x x很大或很小时, f ′ ( x ) f'(x) f′(x)接近于 0 ,会导致梯度很小,权重更新非常缓慢,发生梯度消失问题。 - ReLU函数 修正线性单元(Rectified Linear Unit)
f ( x ) = { x , i f x ≥ 0 0 , i f x < 0 f(x)=\left\{\begin{matrix} x, &if \quad x\geq 0 \\ 0, & if \quad x<0 \end{matrix}\right. f(x)={x,0,ifx≥0ifx<0
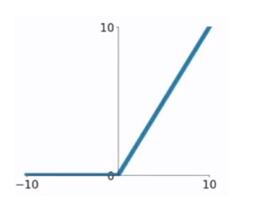
ReLU求导:
f
′
(
x
)
=
{
1
,
i
f
x
>
0
0
,
i
f
x
<
0
f^{'}(x)=\left\{\begin{matrix} 1, &if \quad x> 0 \\ 0, & if \quad x<0 \end{matrix}\right.
f′(x)={1,0,ifx>0ifx<0
ReLU函数的优点:
-
在输入为正数的时候,不存在梯度消失问题;
-
计算速度要快很多。ReLU函数只有线性关系,不管是前向传播还是反向传播,都比sigmod和tanh要快很多(sigmod和tanh要计算指数,计算速度会比较慢)
缺点:
当输入为负时,梯度为0,会产生梯度消失问题; -
Leaky ReLU函数,又称为PReLU函数
f ( x ) = { x , i f x > 0 α x , i f x < 0 f(x)=\left\{\begin{matrix} x, &if \quad x> 0 \\ \alpha x, & if \quad x<0 \end{matrix}\right. f(x)={x,αx,ifx>0ifx<0
其中, α ∈ ( 0 , 1 ) . \alpha \in (0, 1). α∈(0,1).
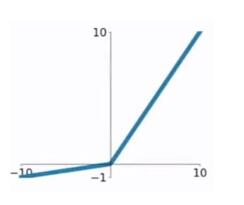
求导:
f
′
(
x
)
=
{
1
,
i
f
x
>
0
α
,
i
f
x
<
0
f^{'}(x)=\left\{\begin{matrix} 1, &if \quad x> 0 \\ \alpha, & if \quad x<0 \end{matrix}\right.
f′(x)={1,α,ifx>0ifx<0
Leaky ReLU函数解决了ReLU函数在输入为负的情况下产生的梯度消失问题。
池化 pooling 的作用
- 缩小参数矩阵的尺寸,从而减少最后全连层中的参数数量。使用池化层即可以加快计算速度也有防止过拟合的作用;
- 保留显著特征,降低特征维度;
- 增大kernel的感受野;
- 提供一定的旋转不变性;
BatchNorm
y k = γ k ⋅ x k − μ k ( σ k ) 2 + ε + β k y^{k}=\gamma^{k} \cdot\frac{x^{k}- \mu ^{k}}{\sqrt{(\sigma^{k})^2+\varepsilon }}+\beta^{k} yk=γk⋅(σk)2+εxk−μk+βk
- 作用:使得每层的输入/输出分布更加稳定,避免参数更新和网络层次变深大幅度影响数据分布。从而使模型训练更稳定。
- 参数 β 和 γ的作用
- 保留网络各层在训练过程中的学习成果
- 保证激活单元的非线性表达能力
- 使批归一化模块具有复原初始输出分布能力
- Batch-normalized 应该放在非线性激活层的前面还是后面?
- 如何区分并记住常见的几种 Normalization 算法
padding 的作用
- 保持边界信息,如果没有加padding的话,输入图片最边缘的像素点信息只会被卷积核操作一次,但是图像中间的像素点会被扫描到很多遍,那么就会在一定程度上降低边界信息的参考程度,但是在加入padding之后,在实际处理过程中就会从新的边界进行操作,就从一定程度上解决了这个问题;
- 可以利用padding对输入尺寸有差异图片进行补齐,使得输入图片尺寸一致;
- 卷积神经网络的卷积层加入Padding,可以使得卷积层的输入维度和输出维度一致;
- 池化层加入padding,可以保持边界信息;
全连接层作用
全连接层在整个卷积神经网络中起到“分类器”的作用。如果说卷积层、池化层和激活函数层等操作是将原始数据映射到隐层特征空间的话,全连接层则起到将学到的“分布式特征表示”映射到样本标记空间的作用,全连接一般会把卷积输出的二维特征图转化成一维的一个向量。
全连接的目的是什么呢?因为传统的网络我们的输出都是分类,也就是几个类别的概率甚至就是一个数–类别号,那么全连接层就是高度提纯的特征了,方便交给最后的分类器或者回归。
softmax
softmax把神经元输出构造成概率分布,而且还起到了归一化的作用,适用于很多需要进行归一化处理的分类问题
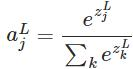
求导

因为softmax中带有指数,实现时极易发生数值不稳定,一旦输入的数特别大,就会导致计算上的溢出,所以一般使用LogSoftmax (然后再求 exp),LogSoftmax少了一个指数计算,少了一个除法,数值上相对稳定一些。

交叉熵 cross entropy
交叉熵刻画的是实际输出 (概率) 与期望输出(概率) 的距离 ,也就是交叉熵的值越小,两个概率分布就越接近。假设概率分布
p
p
p为期望输出,概率分布
q
q
q为实际输出,
H
(
p
,
q
)
H(p,q)
H(p,q)为交叉熵
H
(
p
,
q
)
=
−
∑
x
p
(
x
)
l
o
g
q
(
x
)
H(p,q)=-\sum_{x} p(x)logq(x)
H(p,q)=−x∑p(x)logq(x)


防止过拟合的方法
- early stop
- data augmentation
- dropout dropout在测试时需要将权重乘以
(
1
−
p
)
%
(1-p)\%
(1−p)%

dropout最神奇的地方是,它告诉你,当一个完整的network不做dropout,而是把它的weight乘以(1-p%),把你的training data丢进去,得到的output就是average的值。在这个最简单的case里面,ensemble这件事情跟我们把weight乘以1/2得到一样的结果。但是这个结果只有是linear network才会有这样的结果. - 参数共享
- Batch Normalization
- regularization 正则化
y = b + ∑ w i x i y=b+\sum w_i x_i y=b+∑wixi
L = ∑ n ( y ^ n − ( b + ∑ w i x i ) ) 2 + λ ∑ ( w i ) 2 L=\sum_n (\hat {y}^n-(b+\sum w_ix_i))^2+\lambda \sum (w_i)^2 L=∑n(y^n−(b+∑wixi))2+λ∑(wi)2 正则项
只对 w w w进行正则,因为 b b b反应的是函数的偏移量,对函数的平滑没有影响
正则化
- L1/L2 范数的作用、异同
- 相同点
- 限制模型的学习能力——通过限制参数的规模,使模型偏好于权值较小的目标函数,防止过拟合。
- 不同点
- L1 正则化可以产生更稀疏的权值矩阵,可以用于特征选择,同时一定程度上防止过拟合;L2 正则化主要用于防止模型过拟合
- L1 正则化适用于特征之间有关联的情况;L2 正则化适用于特征之间没有关联的情况。
- 相同点
- 为什么 L1 和 L2 正则化可以防止过拟合?
- L1 & L2 正则化会使模型偏好于更小的权值
- 更小的权值意味着更低的模型复杂度;添加 L1 & L2 正则化相当于为模型添加了某种先验,限制了参数的分布,从而降低了模型的复杂度。
- 模型的复杂度降低,意味着模型对于噪声与异常点的抗干扰性的能力增强,从而提高模型的泛化能力。——直观来说,就是对训练数据的拟合刚刚好,不会过分拟合训练数据(比如异常点,噪声)——奥卡姆剃刀原理
- 为什么 L1 正则化可以产生稀疏权值,而 L2 不会?
- 对目标函数添加范数正则化,训练时相当于在范数的约束下求目标函数 J 的最小值
- 带有L1 范数(左)和L2 范数(右)约束的二维图示
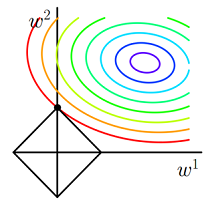
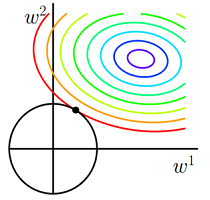
- 图中 J 与 L1 首次相交的点即是最优解。L1 在和每个坐标轴相交的地方都会有“顶点”出现,多维的情况下,这些顶点会更多;在顶点的位置就会产生稀疏的解。而 J 与这些“顶点”相交的机会远大于其他点,因此 L1 正则化会产生稀疏的解。
- L2 不会产生“顶点”,因此 J 与 L2 相交的点具有稀疏性的概率就会变得非常小。
可以使用回归模型解决分类问题吗?直接拟合数据的类别标签

分类问题为什么不像回归问题一样使用均方误差当作损失函数?

逻辑回归的缺点(Logistic Regression)

例如在二维情况下,两个类别分布在两个对角线两端,逻辑回归的分界线只能是一条直线,无法将两个类别分隔开。
解决办法
- 特征转换

- 级联逻辑回归模型

- 级联逻辑回归模型
梯度消失
当网络比较深的时候会出现vanishing Gradient problem
比较靠近input 的几层Gradient值十分小,靠近output的几层Gradient会很大,当你设定相同的learning rate时,靠近input layer 的参数updata会很慢,靠近output layer的参数updata会很快。当前几层都还没有更动参数的时候(还是随机的时候),随后几层的参数就已经收敛了。

网络参数量与计算量的区别与计算
以VGG为例,分析深度网络的计算量和参数量
忽略偏置,则
参数量=Channel_in * Channel_out * Kernel_W * Kernel_W
计算量=Channel_in * Channel_out * Kernel_W * Kernel_W * Feature_map_out_W * Feature_map_out_H
常见的模型加速方法
- 知识蒸馏
- 通道剪枝
- 低秩矩阵分解
- 参数量化





















 2385
2385











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








