PTA排序易错题

最新推荐文章于 2024-12-09 17:57:20 发布

浮而不实

最新推荐文章于 2024-12-09 17:57:20 发布

阅读量1.4w

点赞数 17

分类专栏：算法题

本文链接：https://blog.csdn.net/qq_40989066/article/details/117875381

版权

算法题专栏收录该内容

6 篇文章

订阅专栏

本文深入探讨了比较排序算法中最坏时间复杂度为O(NlogN)的原理，涉及归并排序、快速排序、冒泡排序和选择排序的最坏案例分析，并介绍了不同算法在特定情况下的表现，如归并排序的空间复杂度和稳定性。通过对实际问题的剖析，帮助读者更好地理解算法性能和优化策略。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

仅基于比较的算法能得到的最好的“最坏时间复杂度”是O(NlogN)。
A.对
B.错

原因：常见的最坏的时间复杂度如下第四列，最优是O(NlogN)。
在这里插入图片描述
对N个记录进行归并排序，归并趟数的数量级是O(NlogN)。
A.对
B.错
原因：归并趟数为log2n

对N个记录进行简单选择排序，比较次数和移动次数分别为O(N²)和O(N)
A.对
B.错
原因：简单排序遍历并比较最大的（或最小的）仅仅交换头部与最大或最小的位置，因此比较次数和移动次数分别为O(N²)和O(N)

对N个记录进行快速排序，在最坏的情况下，其时间复杂度是O(NlogN)。
A.对
B.错
原因：顺序逆序时间复杂度为O(N²)

对N个不同的数据采用冒泡排序进行从大到小的排序，当元素基本有序时交换元素次数肯定最多。
A.对
B.错
原因：当元素基本有序时，交换元素元素肯定较少，冒泡和直接插入排序都会较少。

要从50个键值中找出最大的3个值，选择排序比堆排序快。
A.对
B.错
原因：找出元素最大，快速选择就是专门找最大，最小，遍历3遍就解决事情

(neuDS)直接插入排序算法在最好情况下的时间复杂度为O(n)。
A.对
B.错
原因：直接插入与冒泡排序最好都是有序一遍过。

直接选择排序算法在最好情况下的时间复杂度为O（N）
A.对
B.错
原因：直接选择算法，无论如何都需要遍历整个数组选择最大的，比来比去都要O(N²)

快速排序的速度在所有排序方法中为最快，而且所需附加空间也最少。
A.对
B.错
原因：没有绝对最快的算法，只有相对好用的场景，而且部分算法基本上空间复杂度都是O1，而快速排序为log2n。

在待排序数据基本有序的情况下，快速排序效果最好。
A.对
B.错

若数据元素序列{ 11，12，13，7，8，9，23，4，5 }是采用下列排序方法之一得到的第二趟排序后的结果，则该排序算法只能是：
A.冒泡排序
B.选择排序
C.插入排序
D.归并排序
原因：冒泡和选择需要选择最大最小，两边都不是最大最小，直接排除；插入排序符合11，12，13排序符合；归并，看两路归并，13，7不符合，三路也不符合因此只能说插入

数据序列{ 3，2，4，9，8，11，6，20 }只能是下列哪种排序算法的两趟排序结果？
A.冒泡排序
B.选择排序
C.插入排序
D.快速排序
原因：冒泡和选择不符合两边都不是最大最小，直接排除，插入数组开头并未有序，只能是快排

对一组数据{ 2，12，16，88，5，10 }进行排序，若前三趟排序结果如下：第一趟排序结果：2，12，16，5，10，88 第二趟排序结果：2，12，5，10，16，88 第三趟排序结果：2，5，10，12，16，88 则采用的排序方法可能是：
A.冒泡排序
B.希尔排序
C.归并排序
D.基数排序

下面四种排序算法中，稳定的算法是：
A.堆排序
B.希尔排序
C.归并排序
D.快速排序

在基于比较的排序算法中，哪种算法的最坏情况下的时间复杂度不高于O(NlogN)？
A.冒泡排序
B.归并排序
C.希尔排序
D.快速排序
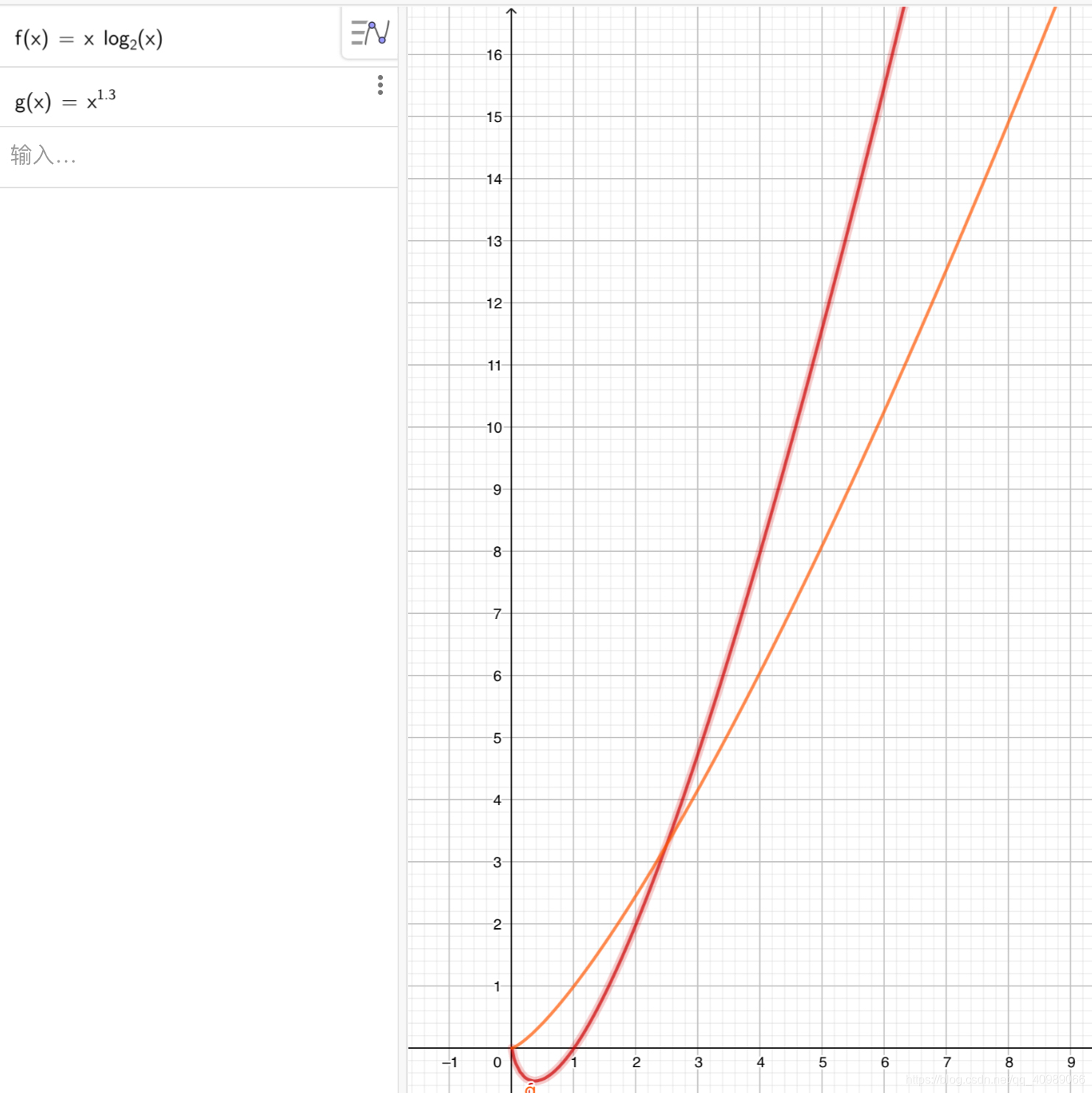
原因：冒泡,快速都是O(N²) 归并是O(NlogN)，希尔平均是N^1.3，下图比较在2-3之后希尔比归并更大，最坏的情况下，且排序比较是多数的比较，因此选择归并更加合理。
在这里插入图片描述
对N个不同的数据采用冒泡算法进行从大到小的排序，下面哪种情况下肯定交换元素次数最多？
A.从小到大排好的
B.从大到小排好的
C.元素无序
D.元素基本有序

对N个记录进行归并排序，空间复杂度为：
A.O(logN)
B.O(N)
C.O(NlogN)
D.O(N2 )
原因：因为考察的是空间复杂度，所以是O(N)

排序方法中，从未排序序列中依次取出元素与已排序序列中的元素进行比较，将其放入已排序序列的正确位置的方法称为：
A.插入排序
B.选择排序
C.快速排序
D.归并排序

设有100个元素的有序序列，如果用二分插入排序再插入一个元素，则最大比较次数是：
A.7
B.10
C.25
D.50
原因：个人小技巧都除以2得到答案，一共除了 2⁷ ，我直接说2⁶ =64<100<2⁷ =128

对一组包含10个元素的非递减有序序列，采用直接插入排序排成非递增序列，其可能的比较次数和移动次数分别是：
A.100, 100
B.100, 54
C.54, 63
D.45, 44
原因：非递减到非递增，有相同情况都是可能，首先考虑正常情况是从第一块数组比较，到最后插入也要比较完所有的数列并且交换，因此从1+…+n -1= (1+n-1)因为直接插入算法是从数组第二位开始比较，因此减少一位（1+9）*9/2 = 45

对N个记录进行快速排序，在最坏的情况下，其时间复杂度是：
A.O(N)
B.O(NlogN)
C.O(N2)
D.O(N2logN)

有组记录的排序码为{46，79，56，38，40，84 }，采用快速排序（以位于最左位置的对象为基准而）得到的第一次划分结果为：
A.{38,46,79,56,40,84}
B.{38,79,56,46,40,84}
C.{38,46,56,79,40,84}
D.{40,38,46,56,79,84}

对于序列{ 49，38，65，97，76，13，27，50 }，按由小到大进行排序，下面哪一个是初始步长为4的希尔排序法第一趟的结果？
A.13,27,38,49,50,65,76,97
B.49,13,27,50,76,38,65,97
C.49,76,65,13,27,50,97,38
D.97,76,65,50,49,38,27,13

给定初始待排序列{ 15，9，7，8，20，-1，4 }。如果希尔排序第一趟结束后得到序列为{ 15，-1，4，8，20，9，7 }，则该趟增量为：
A.1
B.2
C.3
D.4

对N个元素采用简单选择排序，比较次数和移动次数分别为：
A.O(N2), O(N)
B.O(N), O(logN)
C.O(logN), O(N2)
D.O(NlogN), O(NlogN)

对于10个数的简单选择排序，最坏情况下需要交换元素的次数为：
A.9
B.36
C.45
D.100

若数据元素序列{ 12, 13, 8, 11, 5, 16, 2, 9 }是采用下列排序方法之一得到的第一趟排序后的结果，则该排序算法只能是：
A.快速排序
B.选择排序
C.堆排序
D.归并排序
原因：快速排序基准能将12放入左边是绝对有问题，因为只有16才能做，但是周围的排序左右并不分明，因此快排排除，选择两边没有最大最小pass，堆也pass，两路归并符合。

若数据元素序列{ 22, 25, 18, 20, 5, 30, 2, 19 }是采用下列排序方法之一得到的第一趟排序后的结果，则该排序算法只能是：
A.快速排序
B.归并排序
C.堆排序
D.选择排序
原因：如上题

若数据元素序列{ 19, 21, 7, 14, 5, 27, 1, 10 }是采用下列排序方法之一得到的第一趟排序后的结果，则该排序算法只能是：
A.快速排序
B.堆排序
C.归并排序
D.选择排序
原因：如上题

将序列{ 2, 12, 16, 88, 5, 10, 34 }排序。若前2趟排序的结果如下：
第1趟排序后：2, 12, 16, 10, 5, 34, 88
第2趟排序后：2, 5, 10, 12, 16, 34, 88
则可能的排序算法是：
A.冒泡排序
B.快速排序
C.归并排序
D.插入排序

数据序列{ 3, 1, 4, 11, 9, 16, 7, 28 }只能是下列哪种排序算法的两趟排序结果？
A.冒泡排序
B.快速排序
C.插入排序
D.堆排序

设有1000个元素的有序序列，如果用二分插入排序再插入一个元素，则最大比较次数是：
A.1000
B.999
C.500
D.10
原因 2¹⁰ = 1024 > 1000

在内部排序时，若选择了归并排序而没有选择插入排序，则可能的理由是：
归并排序的程序代码更短
归并排序占用的空间更少
归并排序的运行效率更高
A.仅 2
B.仅 3
C.仅 1、2
D.仅 1、3

对初始数据序列{ 8, 3, 9, 11, 2, 1, 4, 7, 5, 10, 6 }进行希尔排序。若第一趟排序结果为（ 1, 3, 7, 5, 2, 6, 4, 9, 11, 10, 8 ），第二趟排序结果为（ 1, 2, 6, 4, 3, 7, 5, 8, 11, 10, 9 ），则两趟排序采用的增量（间隔）依次是：
A.3, 1
B.3, 2
C.5, 2
D.5, 3
原因：第一趟1和6和8进行插入排序，因此算下来增量为5，第二趟2与3互换且增量减少，因此算下为3

7-1 英文单词排序 (25 分)
本题要求编写程序，输入若干英文单词，对这些单词按长度从小到大排序后输出。如果长度相同，按照输入的顺序不变。

输入格式：
输入为若干英文单词，每行一个，以#作为输入结束标志。其中英文单词总数不超过20个，英文单词为长度小于10的仅由小写英文字母组成的字符串。

输出格式：
输出为排序后的结果，每个单词后面都额外输出一个空格。

输入样例：

blue
red
yellow
green
purple
#

输出样例：

red blue green yellow purple

代码c++

#include "iostream"
#include "string"
#define MAXSIZE 50
using namespace std;

struct SqList{
    string data[MAXSIZE];
    int length;
};

SqList initSqlist(){
    SqList sqList;
    sqList.length = 0;
    string tmp;
    while (tmp != "#"){
        cin >> tmp;
        if (tmp == "#"){
            break;
        }
        sqList.data[sqList.length++] = tmp;
    }
    return sqList;
}

void swap_num(string &a, string &b){
    string tmp = a;
    a = b;
    b = tmp;
}

void BubbleSort(SqList *sqList){
    for (int i = 0; i < sqList->length ; ++i) {
        bool flag = false;
        for (int j = 0; j < sqList->length -1; j++) {
            if (sqList->data[j].size() > sqList->data[j+1].size()){
                swap_num(sqList->data[j], sqList->data[j+1]);
                flag = true;
            }
        }
        if (flag == false){
            return;
        }
    }
}

void printList(SqList *sqList){
    for (int i = 0; i < sqList->length; ++i) {
        cout << sqList->data[i] << " ";
    }
}

int main(){
    SqList sqList = initSqlist();
    BubbleSort(&sqList);
    printList(&sqList);
    return 0;
}

冒泡法排序 (20 分)
将N个整数按从小到大排序的冒泡排序法是这样工作的：从头到尾比较相邻两个元素，如果前面的元素大于其紧随的后面元素，则交换它们。通过一遍扫描，则最后一个元素必定是最大的元素。然后用同样的方法对前N−1个元素进行第二遍扫描。依此类推，最后只需处理两个元素，就完成了对N个数的排序。

本题要求对任意给定的K（<N），输出扫描完第K遍后的中间结果数列。

输入格式：
输入在第1行中给出N和K（1≤K<N≤100），在第2行中给出N个待排序的整数，数字间以空格分隔。

输出格式：
在一行中输出冒泡排序法扫描完第K遍后的中间结果数列，数字间以空格分隔，但末尾不得有多余空格。

输入样例：

6 2
2 3 5 1 6 4

输出样例：

2 1 3 4 5 6

代码 c++

#include "iostream"
using namespace std;
#define MAXSIZE 101
struct SqList{
    int data[MAXSIZE];
    int length;
};

SqList initSList(int N){
    SqList sqList;
    sqList.length = 0;
    int tmp;
    for (int i = 0; i < N; ++i) {
        cin >> tmp;
        sqList.data[sqList.length++] = tmp;
    }
    return sqList;
}

void swap_num(int &a, int &b){
    int tmp = a;
    a = b;
    b = tmp;
}

void BubbleSort(SqList *sqList,int times){
    for (int i = 0; i < times ; ++i) {
        bool flag = false;
        for (int j = 0; j < sqList->length -1; j++) {
            if (sqList->data[j] > sqList->data[j+1]){
                swap_num(sqList->data[j], sqList->data[j+1]);
                flag = true;
            }
        }
        if (flag == false){
            return;
        }
    }
}

void printList(SqList sqList){
    for (int i = 0; i < sqList.length; ++i) {
        if (i == sqList.length - 1){
            cout << sqList.data[i];
        } else{
            cout << sqList.data[i] << " ";
        }
    }
}

int main(){
    int N,times;
    cin >> N;
    cin >> times;
    SqList sqList = initSList(N);
    BubbleSort(&sqList,times);
    printList(sqList);
    return 0;
}