监督学习-单变量线性回归模型

最新推荐文章于 2022-12-02 17:21:12 发布

Civitasv

最新推荐文章于 2022-12-02 17:21:12 发布

阅读量607

点赞数 1

分类专栏： Neural network 文章标签： Machine learning Gradient descent linear regression Supervised learning Cost function

本文链接：https://blog.csdn.net/qq_40996400/article/details/87936224

版权

Neural network 专栏收录该内容

9 篇文章 0 订阅

订阅专栏

监督学习是机器学习中很重要的一种类型，还不理解什么是机器学习？机器学习概述

单变量线性回归是监督学习回归问题算法中最简单的一种类型之一，理解了这个模型，我们就能大致理解监督学习是在做什么了。首先，我们做以下规定：

$m$ : 表示训练样本个数

$x$ ：输入变量

$y$ ：输出变量

$(x,y)$ ：一个训练样本

$({x}^{(i)},{y}^{(i)})$ ：第 $i$ 个训练样本

$h$ ：目标函数，映射 $x\rightarrow y$

以预测房价例子入手，模型简化，仅把面积作为房价的依据，我们需要实现下图所示功能，使用监督学习算法，获得目标函数，通过给定的房屋面积，预测房屋价格。因为此时仅有一个面积数据制约着房价，所以这个模型即为单变量线性回归模型。此时我们一般把目标函数定义为 ${h}_{\Theta }(x) = \Theta_0+\Theta _1x$ 。

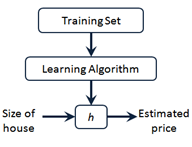
（从吴恩达老师的课程摘取获得）

将我的Traing set在matlab上用散点图显示如下：

注：数据来源为吴恩达老师课程文件

可以明显看出点大致分布在一条直线周围。此时样本数 $\small m$ = 97。

我们要获得这条拟合直线，就要获得 $\small \Theta_0$ 和 $\small \Theta _1$ 的值。这两个值的选择思路是获得与散点图最为拟合的一条直线，这时要确保与 $y$ 值相差最小（这一点可以理解为使残差最小），这时我们就需要引入代价函数，也称为平方误差函数、均方误差函数。

代价函数的函数公式为：

$\small J(\Theta _0,\Theta _1) = (1/2m)\sum_{i=1}^{m}(h_\Theta (x^{(i)})-y^{(i)})^2$

代价函数是解决回归问题的常用手段。上面提到了我们需要获得使残差最小的 $\small \Theta _0$ 和 $\small \Theta _1$ ，所以我们要获得使代价函数最小的 $\small \Theta _0$ 和 $\small \Theta _1$ 。使用matlab作出代价函数的三维曲面图：

这时我们可以明显的看出三维平面内代价函数 $\small J(\Theta _0,\Theta _1)$ 存在最小值点。这个点所对应的 $\small \Theta _0$ 和 $\small \Theta _1$ 即是我们要求的值。这个时候，我们就不得不考虑另一个问题了，如何求这个最小值点？事实上，我们是可以使用高等数学导数知识求解的，但较为麻烦，本博客中不作介绍，我们换一种思路。在解答这个问题之前，我想先引入一个算法-梯度下降算法（Gradient descent）。

梯度下降算法被广泛应用于求函数（不仅仅可以两个变量）的最小值所对应的自变量值中。数学形式为：

repeat until convergence{

$\small \Theta _j := \Theta _j-\alpha *(\frac{\partial J(\Theta _0,\Theta _1,...\Theta _n)}{\partial \Theta _j})$ $\small \dpi{100} \fn_cm j = 0,1,2,3 ... n$

}

这里要注意一点， $\small \Theta _0,\Theta _1,...\Theta _n$ 必须同时更新，以两个变量为例：

$\small temp0 := \Theta _0-\alpha *(\frac{\partial J(\Theta _0,\Theta _1)}{\partial \Theta _0})$

$\small temp1 := \Theta _1-\alpha *(\frac{\partial J(\Theta _0,\Theta _1)}{\partial \Theta _1})$

$\small \Theta _0 := temp0$

$\small \Theta _1 := temp1$

其中 $\large \alpha$ 被称为学习速率（大于0），不能过大，也不能过小。通过一次次的更新循环， $\small \Theta _j$ 逐渐靠近代价函数最小值所对应的坐标点所对应的 $j$ 维度（感觉可以这样用？大家理解就好）的值。明确一点，梯度下降法是可以求出最优解的，这个最优解包括局部最优解或是全局最优解，达到最优解则返回。

以单变量线性回归模型解释下上面这个式子为什么能够逐步逼近最优解，置 $\small \Theta _0$ 为0，此时 ${h}_{\Theta }(x) = \Theta _1x$ （过原点），则代价函数的函数图像为：

这是一个二次函数，假设我从最低点的右侧开始寻找，此时微分式大于0，而学习速率大于0，所以 $\small \Theta _1$ 就会向左移动，逼近最低点，若从最低点的左侧开始寻找，此时微分式小于0，所以 $\small \Theta _1$ 会向右移动，逼近最低点。如果学习速率过大，移动步长就会过大，甚至第一次就会超过最低点，所以不可取，如果学习速率过小，移动步长过小，算法效率就会很低，不可取。

到这里，我们就可以回答上面那个问题了，在单变量线性回归模型中，我们可以使用梯度下降算法获得代价函数最小值点对应的 $\small (\Theta _0,\Theta _1)$ 。这里给出结论：

$\small temp0 := \Theta _0-\alpha *\frac{1}{m} \sum_{i=1}^{m}(\Theta _0+\Theta _1x^{(i)}-y^{(i)})$

$\small temp1 := \Theta _1-\alpha *\frac{1}{m} \sum_{i=1}^{m}((\Theta _0+\Theta _1x^{(i)}-y^{(i)})*x^{(i)})$

$\small \Theta _0 := temp0$

$\small \Theta _1 := temp1$

由于代价函数是一个凹函数，此时并不存在局部最优解，仅存在一个全局最优解。

以上散点数据和三维曲面图生成均在matlab中进行，数据和脚本代码被我上传到了github上。

参考：吴恩达老师课程

Civitasv

关注

1
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
监督学习-单变量线性回归模型

监督学习是机器学习中很重要的一种类型，还不理解什么是机器学习？机器学习概述单变量线性回归是监督学习回归问题算法中最简单的一种类型之一，理解了这个模型，我们就能大致理解监督学习是在做什么了。首先，我们做以下规定：: 表示训练样本个数：输入变量：输出变量：一个训练样本：第个训练样本：目标函数，映射以预测房价例子入手，模型简化，仅把面积作为房价的依据，我们需要实现下图所示...
复制链接

扫一扫